Modulus Transformations (DP IB Analysis & Approaches (AA)): Revision Note

Modulus transformations

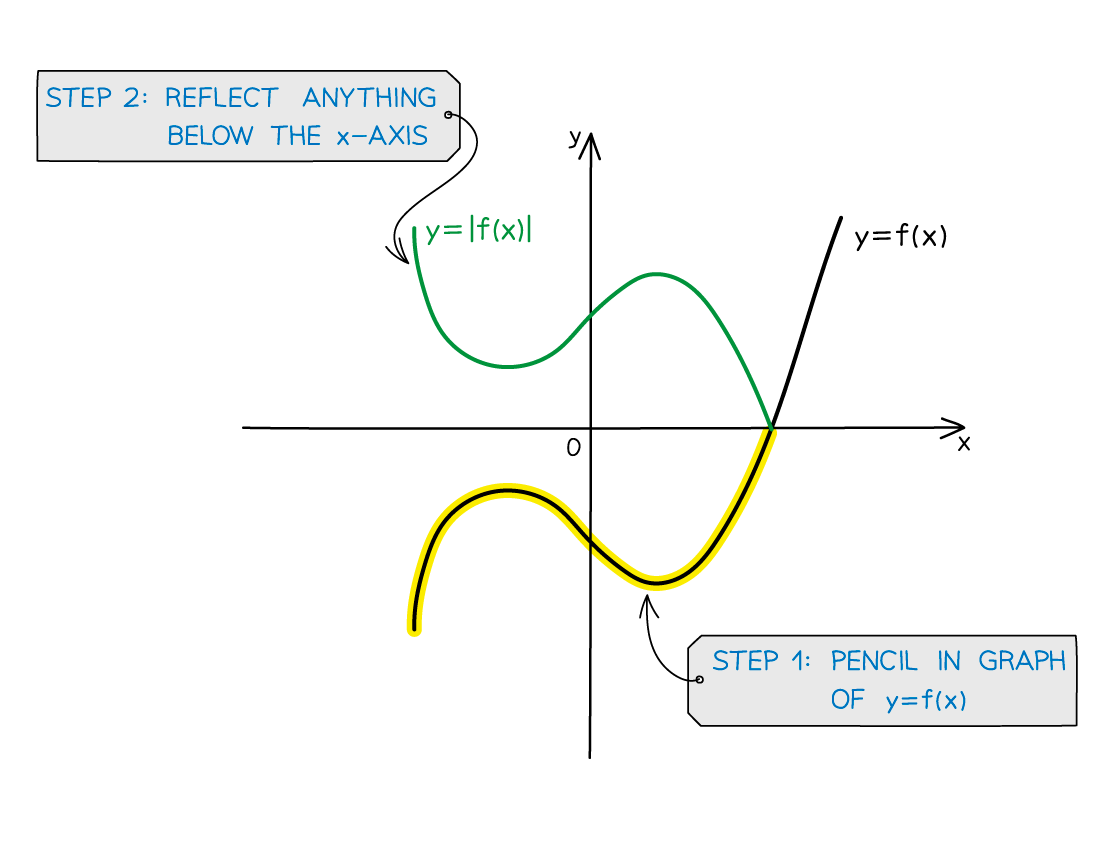
How do I sketch the modulus of a function y = |f(x)|?

• To sketch

  • STEP 1
    Sketch the parts of that are on or above the -axis

  • STEP 2
    Sketch the reflections in the -axis of any parts below

How do I sketch a function of mod x, y = f(|x|)?

• To sketch

  • STEP 1
    Keep the part of on, or to the right of, the -axis

    • get rid of any part that is to the left

  • STEP 2

    Reflect the right-hand side in the -axis to create a left-hand side

    • This will create a symmetric graph about the -axis

What are some differences between y = |f(x)| or y = f(|x|)?

• It helps to remember that

  • can never go below the -axis

    • whereas can

  • is always symmetric about the -axis

    • whereas does not have to have any lines of symmetry

How do I sketch transformations of y = |f(x)|?

• To sketch

  • first sketch without modulus signs

  • then apply a vertical stretch of scale factor

    • 

  • followed by a vertical translation of

    • 

  • then take the modulus (using the rules above)

    • 

• To sketch

  • sketch (as above)

  • then apply a vertical stretch of scale factor

    • 

  • followed by a vertical translation of

    • 

How do I sketch transformations of y = f(|x|)?

• To sketch

  • sketch (using the rules above)

  • then apply a vertical stretch of scale factor

    • 

  • followed by a vertical translation of

    • 

How do I sketch y = |f(ax+b)| or y = f(|ax+b|)?

• To sketch

  • first sketch which factorises to

    • i.e. first apply a horizontal stretch to of scale factor

    • becomes

    • followed by a horizontal translation of to the left,

    • i.e. becomes which is

  • then take the modulus of using the rules above

    • 

• To sketch

  • factorise it to

    • i.e. first apply a horizontal stretch of scale factor to

    • becomes

    • followed by a horizontal translation of to the left,

    • i.e. becomes which is