Factorising Quadratics (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Factorising quadratics
Why is factorising quadratics useful?
Factorising gives roots (zeroes or solutions) of a quadratic
It gives the
-intercepts of the graph of the quadratic
How do I factorise a monic quadratic of the form x2+bx+c?
A monic quadratic is a quadratic where the coefficient of the
term is 1
You might be able to spot the factors by inspection
Especially if
is a prime number
Otherwise, start by finding two numbers
and
which have,
A sum equal to
A product equal to
Rewrite the middle term of the quadratic,
, as
Use this to factorise
A shortcut is to write down
as soon as you have found
and
Worked Example
Factorise fully.

How do I factorise a non-monic quadratic of the form ax2+bx+c?
A non-monic quadratic is a quadratic where the coefficient of the
term is not equal to 1
If
,
and
have a common factor then first factorise that out to leave a quadratic with coefficients that have no common factors
E.g.
can be rewritten as
You might be able to spot the factors by inspection
Especially if
and/or
are prime numbers
Otherwise, start by finding two numbers
and
which have,
A sum equal to
A product equal to
Rewrite the middle term,
, as
Use this to factorise
A shortcut is to write
Then factorise common factors from numerator to cancel with the a on the denominator
Worked Example
Factorise fully.
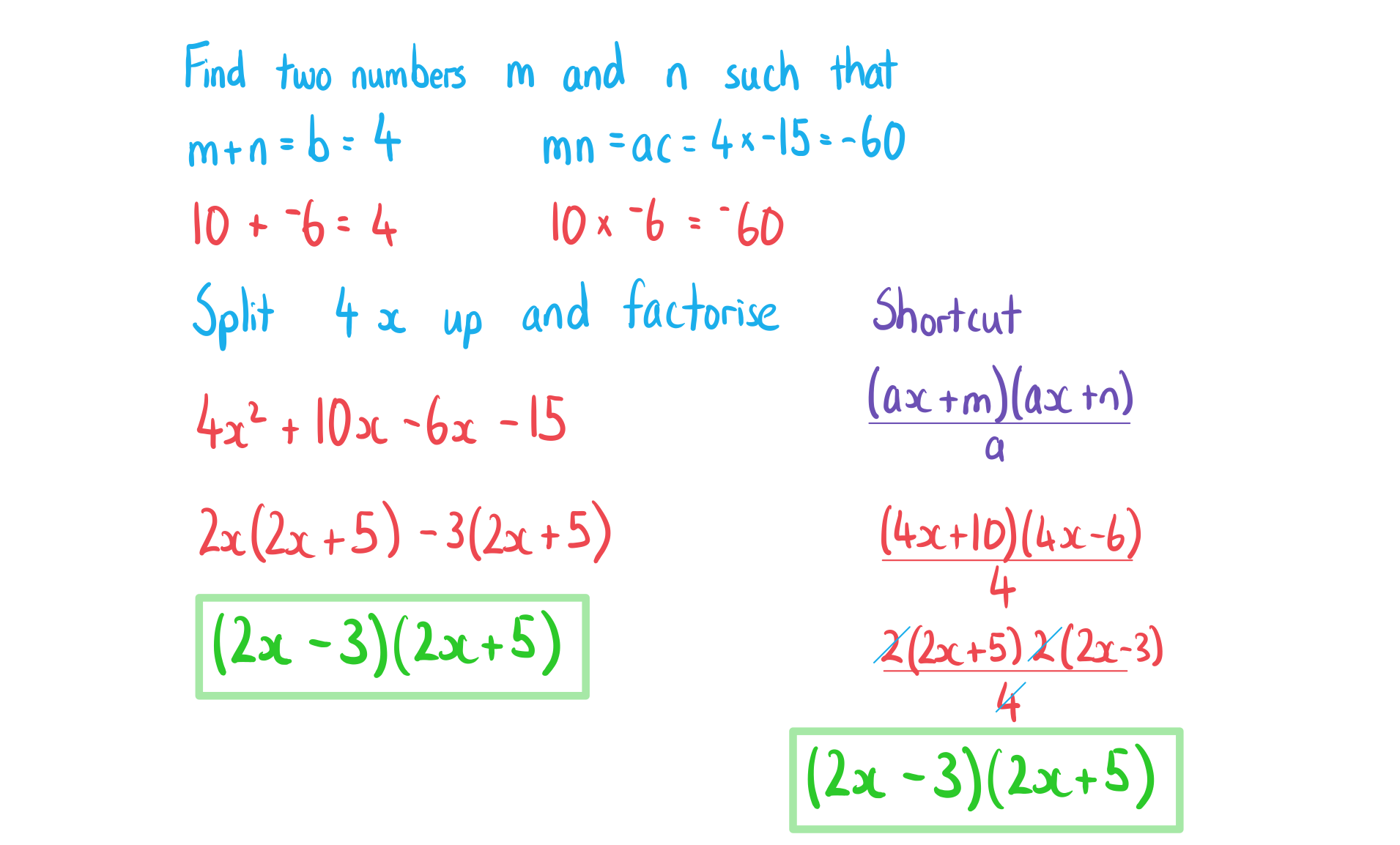
How do I use the difference of two squares to factorise a quadratic of the form a2x2-c2?
The difference of two squares can be used when
There is no linear
term and
The constant term is a negative
E.g.
First, square-root the two terms
and
The two factors of the quadratic are the sum of the square roots and the difference of the square roots
i.e.
Worked Example
Factorise fully.

Examiner Tips and Tricks
You can deduce the factors of a quadratic function by using your GDC to find the solutions of a quadratic equation.
Using your GDC, the quadratic equation has solutions
and
.
Therefore the factors would be and
.
i.e. .

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?