Composite Transformations of Graphs (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Composite transformations of graphs
What transformations do I need to know?
is horizontal translation by vector
If
is positive then the graph moves right
If
is negative then the graph moves left
is horizontal translation by vector
If
is positive then the graph moves left
If
is negative then the graph moves right
is vertical translation by vector
If
is positive then the graph moves up
If
is negative then the graph moves down
is a horizontal stretch by scale factor
parallel to the
-axis
If
then the graph gets closer to the
-axis
If
then the graph gets further from the
-axis
is a vertical stretch by scale factor
parallel to the
-axis
If
then the graph gets further from the
-axis
If
then the graph gets closer to the
-axis
is a horizontal reflection about the
-axis
is a vertical reflection about the
-axis
Does the order of transformations matter?
The order of applying transformations does matter
In general
different horizontal transformations need to be applied in order
different vertical transformations need to be applied in order
but horizontal and vertical transformations can swap orders
They are independent of each other
e.g. if there are two horizontal transformations H1 then H2 and two vertical transformations V1 then V2
then the following orders are all acceptable
Horizontal then vertical: H1 H2 V1 V2
Vertical then horizontal: V1 V2 H1 H2
Mixed up (but H1 before H2 and V1 before V2):
H1 V1 H2 V2
H1 V1 V2 H2
V1 H1 V2 H2
V1 H1 H2 V2
Examiner Tips and Tricks
When splitting a harder transformation into a sequence of single transformations, it helps to sketch the graph at each stage in the sequence.
Worked Example
The diagram below shows the graph of .
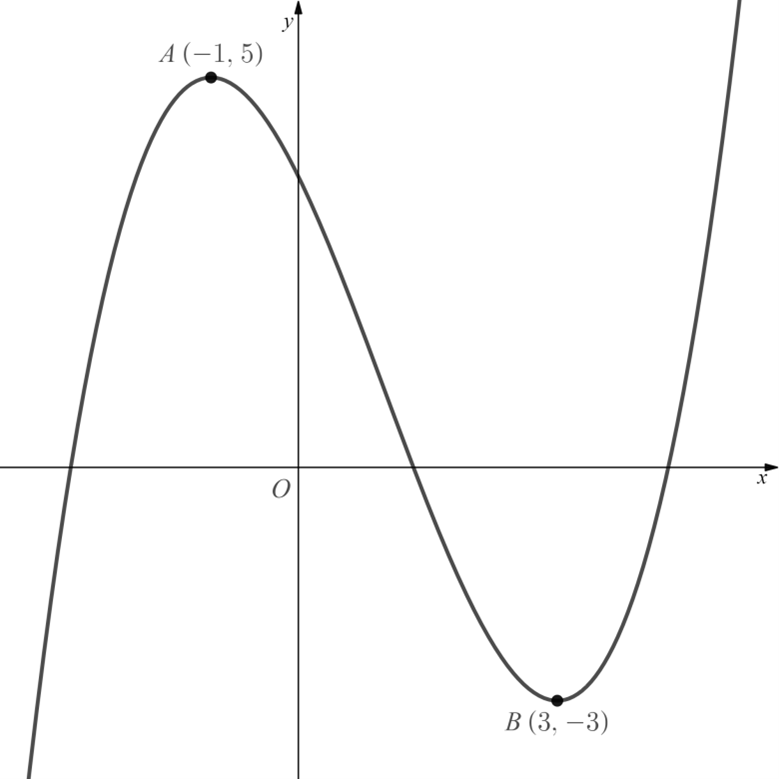
Sketch the graph of .
Did this video help you?
Composite vertical transformations af(x)+b
What does the transformation af(x)+b represent?
The transformation
represents, in order:
a vertical stretch of
by scale factor
followed by a translation of
giving
It is not a translation of
followed by a vertical stretch by scale factor
because that would give
translation:
then stretch:
final equation:
If
is negative, then there is also a reflection in the
-axis
either before or after the vertical stretch
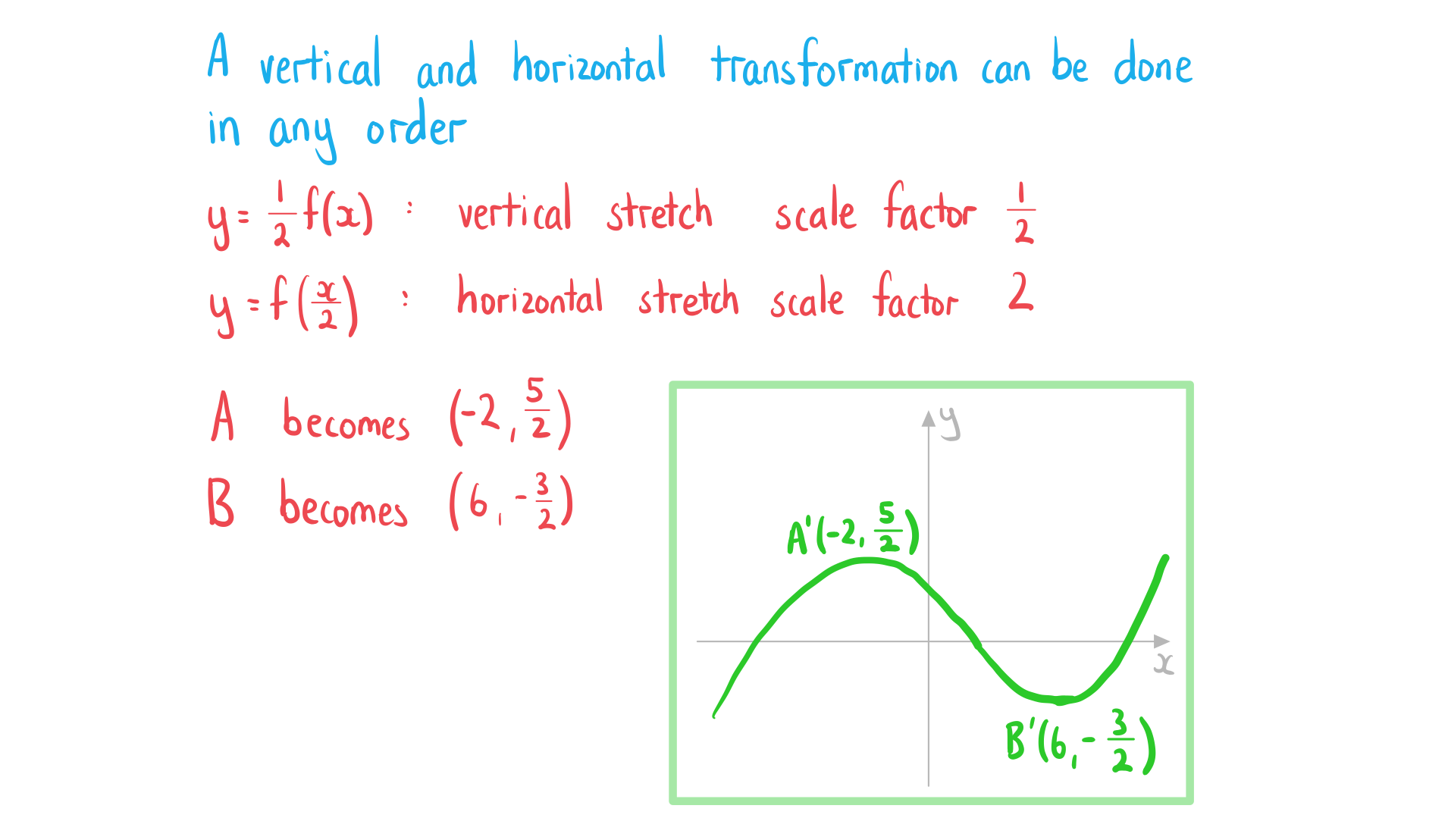
Worked Example
The diagram below shows the graph of .

Sketch the graph of .
Did this video help you?
Composite horizontal transformations f(ax+b)
What does the transformation f(ax+b) represent?
The transformation
represents, in order:
a translation of
by
followed by a horizontal stretch by scale factor
giving
It is not a horizontal stretch by scale factor
followed by a translation of
because that would give
stretch:
then translation:
final equation:
If
is negative, then there is also a reflection in the
-axis
either before or after the horizontal stretch
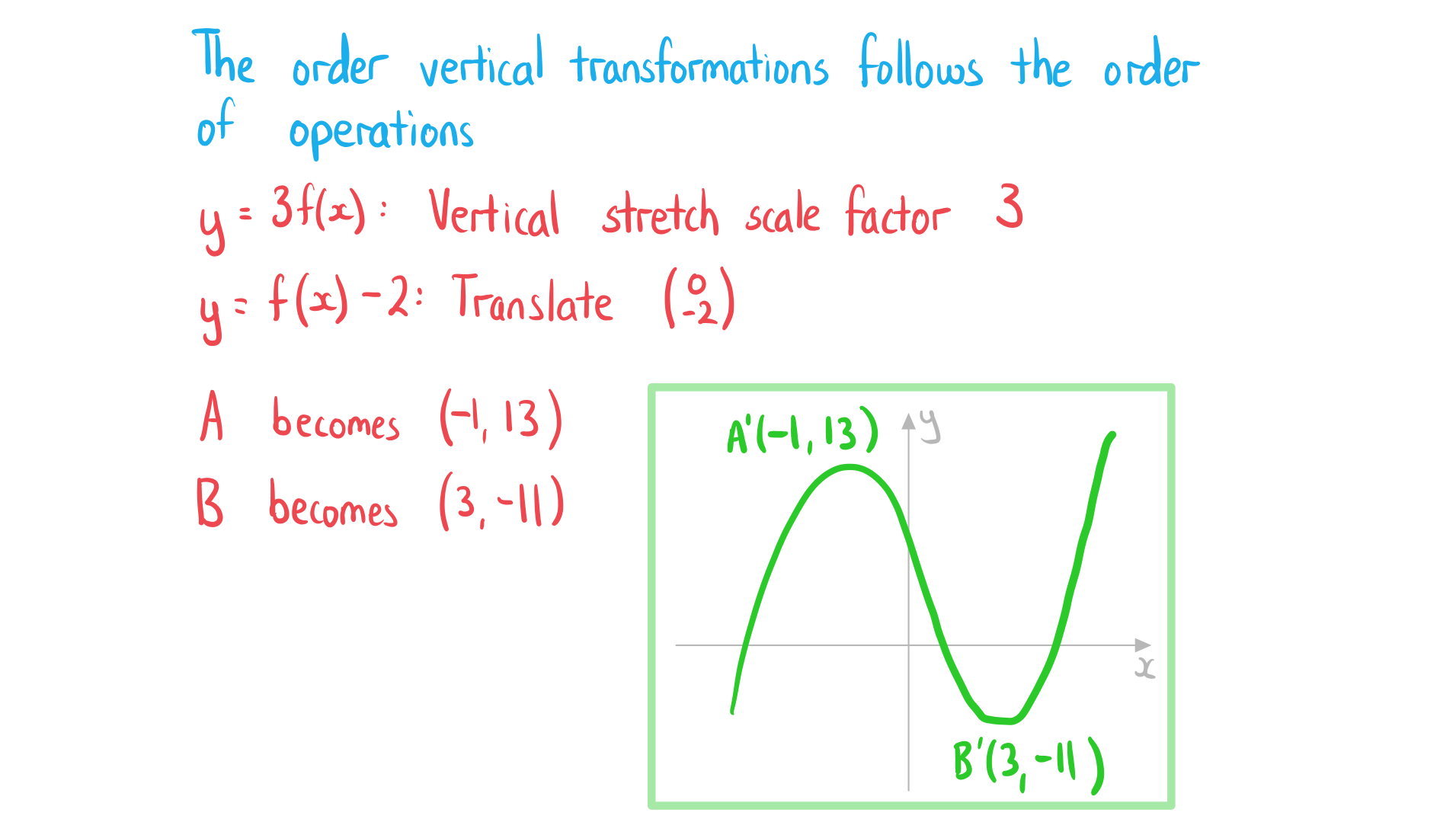
Worked Example
The diagram below shows the graph of .

Sketch the graph of .

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?