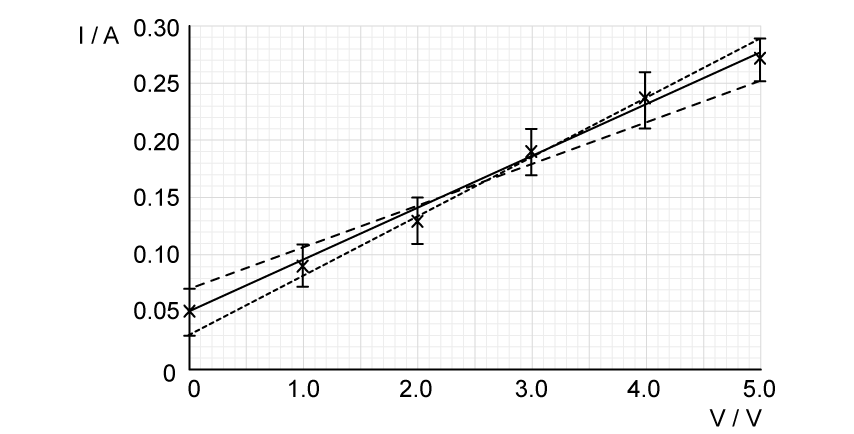
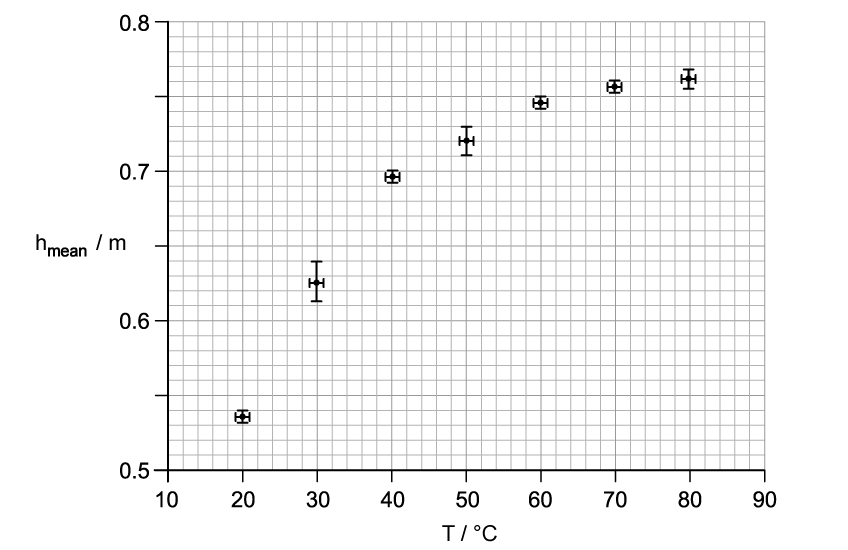
Newton's second law of motion can be written as
where is force,
is mass, and
is acceleration.
Using Newton's second law, deduce the fundamental SI units of .
The kinetic energy equation can be written as
where is kinetic energy,
is mass, and
is velocity.
Using the kinetic energy equation, deduce the fundamental SI units of energy .
The derived unit of power is the watt (W).
Derive the unit of power in terms of fundamental SI units.
Did this page help you?