Continuity & Differentiability (DP IB Analysis & Approaches (AA)): Revision Note

Continuity & differentiability

What does it mean for a function to be continuous at a point?

• If a function is continuous at a point then the graph of the function does not have any ‘holes’ or any sudden ‘leaps’ or ‘jumps’ at that point

  • Imagine sketching the graph

    • If you can sketch the graph without lifting your pencil from the paper, then the function is continuous at all the points that your sketch goes through

    • But if you would have to lift your pencil off the paper at some point and continue drawing the graph from another point, then the function is not continuous at any such points where the function ‘jumps’

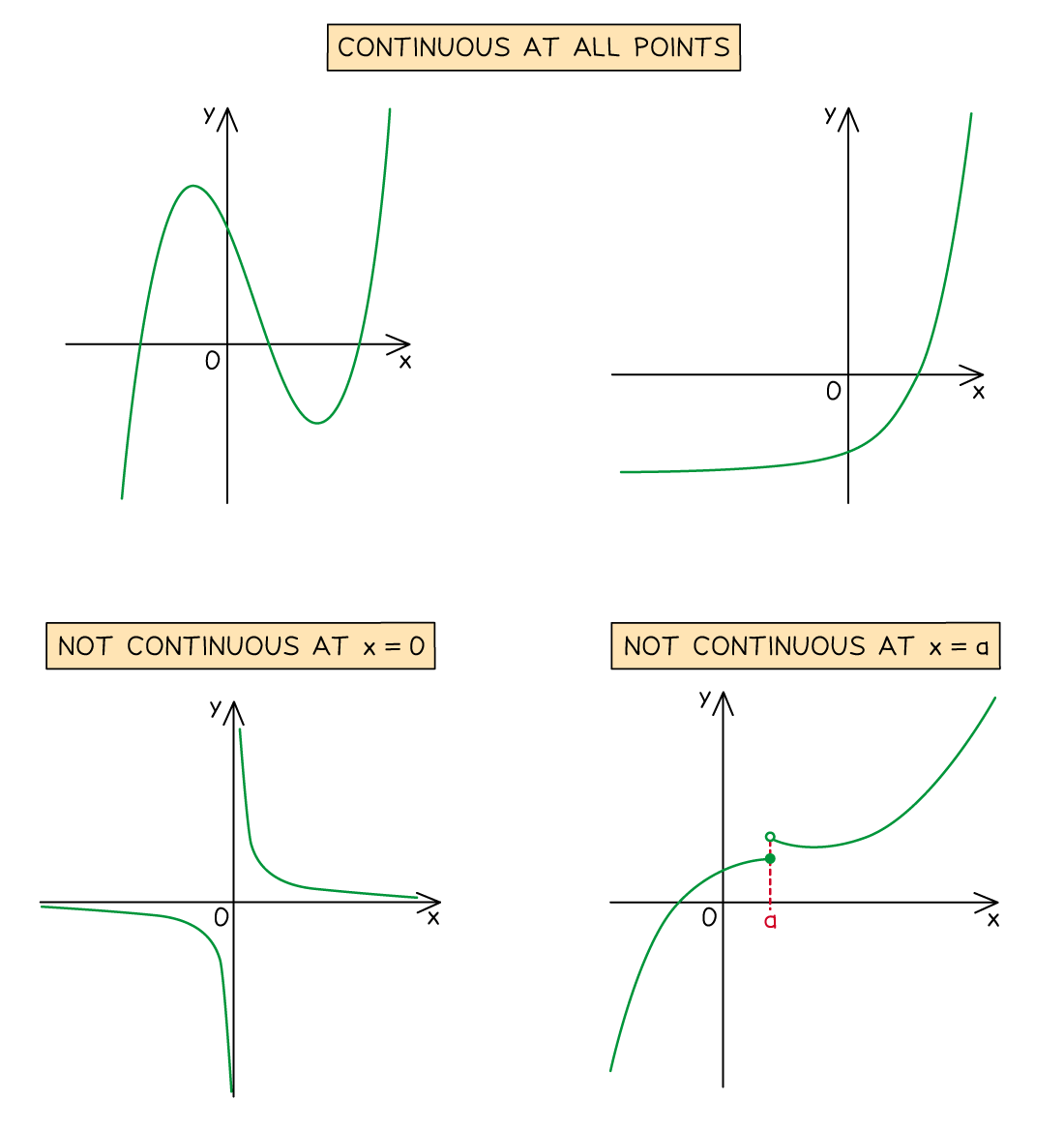
• There are two main ways a function can fail to be continuous at a point:

  • If the function is not defined for a particular value of x then it is not continuous at that value of x

    • For example,   is not continuous at x = 0

  • If the function is defined for a particular value of x, but then the value of the function ‘jumps’ as x moves away from that x value (in the positive or negative direction), then the function is not continuous at that value of x

    • This type of discontinuity can occur in a piecewise function, for example, where the different pieces of the function’s graph don’t ‘join up’

• You can use limits to show that a function is continuous at a point

  • Let f(x) be a function defined at x = a, such that f(a) = b

    • If and , then f(x) is continuous at x = a

    • If either of those limits is not equal to b, then f(x) is not continuous at x = a

  • This is a slightly more formal way of expressing the ‘you don’t have to lift your pencil from the paper’ idea!

What does it mean for a function to be differentiable at a point?

• We say that a function f(x) is differentiable at a point with x-coordinate x₀, if the derivative f’(x) exists and has a well-defined value f’(x₀) at that point

• To be differentiable at a point a function has to be continuous at that point

  • So if a function is not continuous at a point, then it is also not differentiable at that point

• But continuity by itself does not guarantee differentiability

  • Differentiability is a stronger condition than continuity

    • If a function is differentiable at a point, then the function is also continuous at that point

    • But a function may be continuous at a point without being differentiable at that point

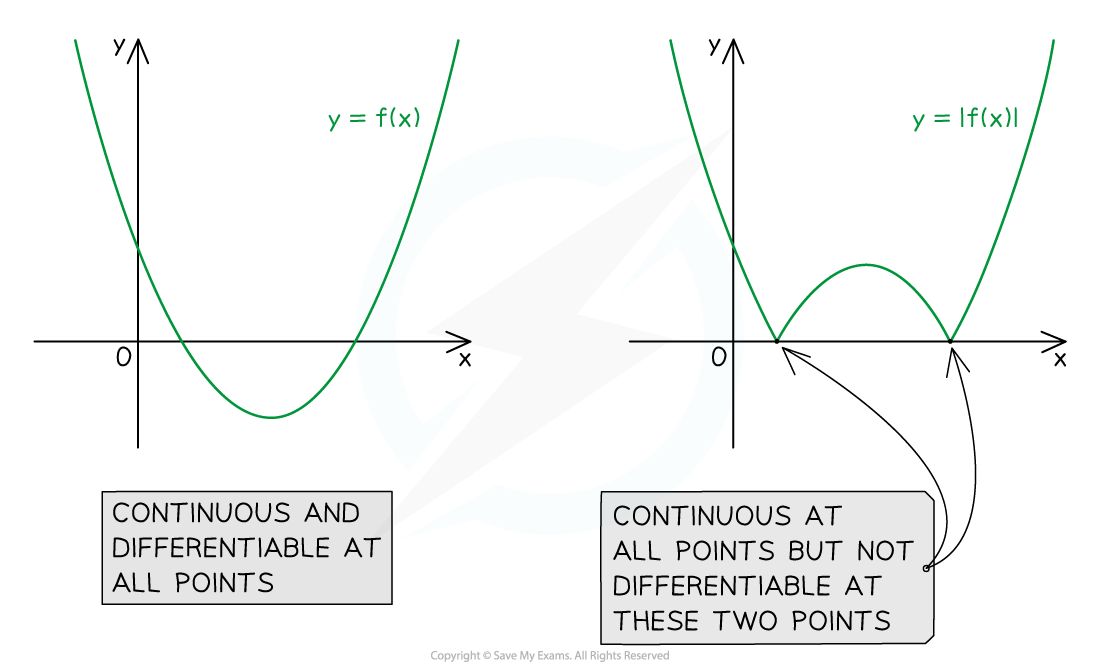
  • So a function may be continuous everywhere but not differentiable everywhere

• In addition to being continuous a point, differentiability also requires that the function be smooth at that point

  • ‘Smooth’ means that the graph of the function does not have any ‘corners’ or sudden changes of direction at the point

  • An obvious example of a function that is not smooth at certain points is a modulus function |f(x)| at any values of x where f(x) changes sign from positive to negative

    • At any such point a modulus function will not be differentiable