Modelling with Volumes of Revolution (DP IB Analysis & Approaches (AA)): Revision Note
Adding & subtracting volumes
When would volumes of revolution need to be added or subtracted?
The ‘curve’ boundary of an area may consist of more than one function of
For example
the ‘curve’ boundary from
to
is
the ‘curve’ boundary from
to
is
So the total volume would be
The solid of revolution may have a ‘hole’ in it
e.g. a ‘toilet roll’ shape would be the difference of two cylindrical volumes
Examiner Tips and Tricks
The volume of the solid of revolution formed by rotating an area through radians around the
-axis is
, and for the
-axis is
. These are both given in the exam formula booklet.
How do I know whether to add or subtract volumes of revolution?
When the area to be rotated around the
-axis has more than one function defining its boundary it can be trickier to tell whether to add or subtract volumes of revolution
It will depend on the nature of the functions and their points of intersection
Sketch the graph of the functions (using your GDC where possible) and highlight the area required
How do I solve problems involving adding or subtracting volumes of revolution?
Visualising the solid created becomes increasingly useful (but also trickier) for shapes generated by separate volumes of revolution
Continue trying to sketch the functions and their solids of revolution to help
STEP 1
Identify the functions
involved in generating the volume
Determine whether the separate volumes will need to be added or subtracted
Identify the limits for each volume involved
Sketching the graphs of
and
, or using a GDC to do so, is helpful, especially when the limits are not given directly in the question
STEP 2
Square
for all functions
This step is not essential if a GDC can be used to calculate integrals and an exact answer is not required.
STEP 3
Using the appropriate volume of revolution formula for each part, evaluate the definite integral and add or subtract as necessary
The answer may be required in exact form
Examiner Tips and Tricks
A sketch of the graph, limits, etc. is always helpful, whether one has been given in the question or not. Use your GDC where possible.
Worked Example
Find the volume of revolution of the solid formed by rotating the region enclosed by the positive coordinate axes and the graphs of and
by
radians around the
-axis. Give your answer to three significant figures.

Modelling with volumes of revolution
What is meant by modelling volumes of revolution?
Many everyday objects such as buckets, beakers, vases and lampshades can be modelled as solids of revolution
The volume of revolution of the solid can then be calculated
An object that would usually stand upright may be modelled horizontally so its volume of revolution can more easily be found
What modelling assumptions are there with volumes of revolution?
The solids formed are usually the main part of the body of the object
For example, the handle on a bucket would not be included
For something like a bucket or drinking glass, the thickness of the walls of the object is usually assumed to be negligible relative to the size of the object
Thickness will depend on the purpose of the object and the material it is made from
How do I solve modelling problems with volumes of revolution?
Visualising and sketching the solid formed can help with starting problems
Be familiar with applying the volume of revolution formulas
around the x-axis:
around the y-axis:
The volume of revolution may involve adding or subtracting partial volumes
Questions may ask related questions in context
E.g. a question about a bucket may ask about its capacity
this would be measured in litres
so a conversion of units may be required
(1000 cm3 = 1 litre)
Examiner Tips and Tricks
Remember to answer questions based on their context. In modelling scenarios, interpretation is often needed after finding the 'final answer'.
Modelling questions often ask about assumptions, criticisms and/or improvements. For example:
It is assumed the thickness of the material an object is made from is negligible
A 'smooth' curve may not be a good model if the item is being made from a rough material
Other things may significantly reduce the volume found and impact conclusions
E.g. stones, plants and decorations placed in an aquarium will reduce the volume of water needed to fill it - and hence the number/size/type of fish it can accommodate may be impacted
Worked Example
The diagram below shows the region R, which is bounded by the function , the lines
and
, and the
-axis.
Dimensions are in centimetres.
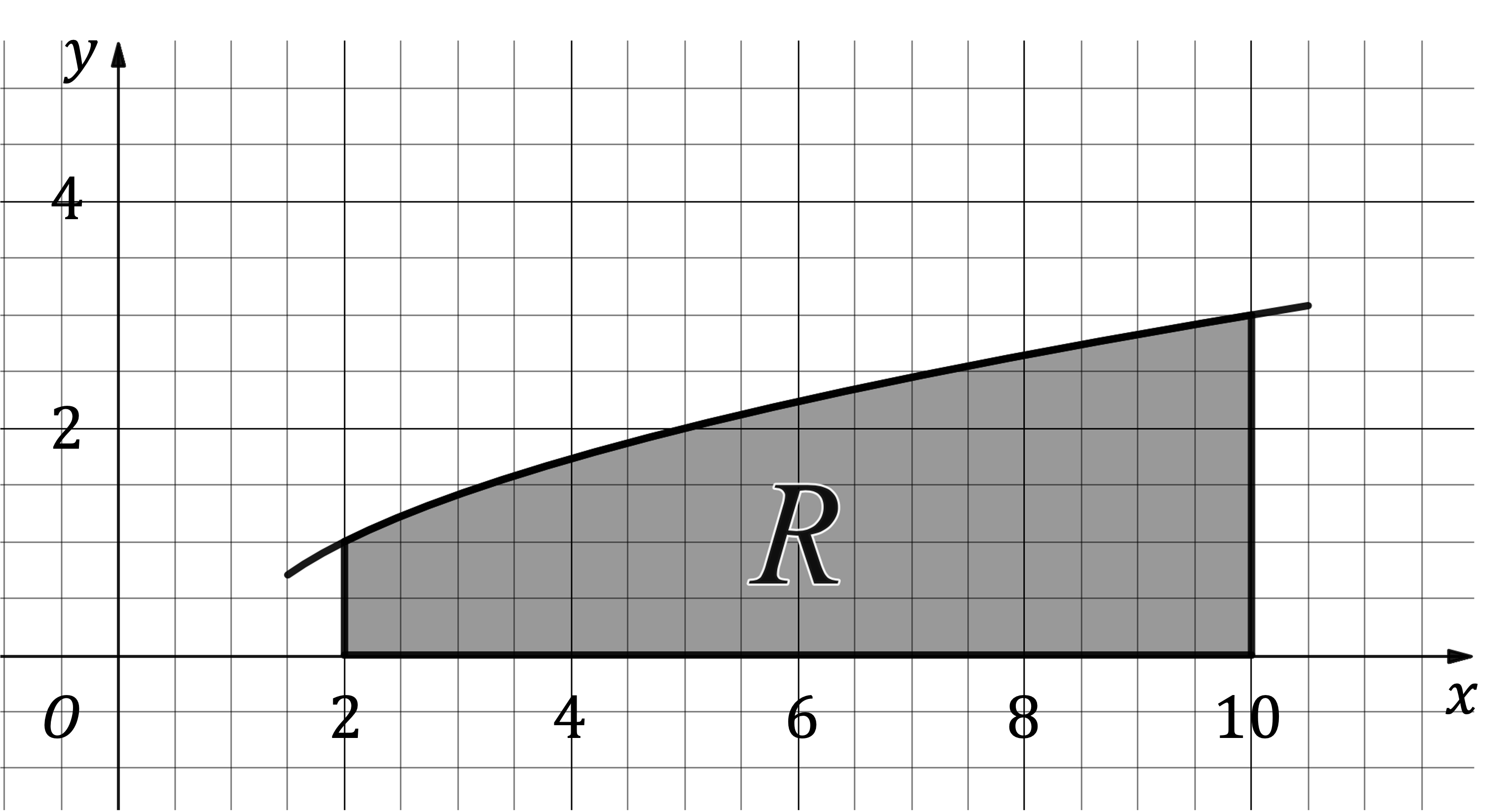
A mathematical model for a miniature vase is produced by rotating the region R through radians around the x-axis.
Find the volume of the miniature vase, giving your answer in litres to three significant figures.


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?

