Increasing & Decreasing Functions (DP IB Analysis & Approaches (AA)): Revision Note

Increasing & Decreasing Functions

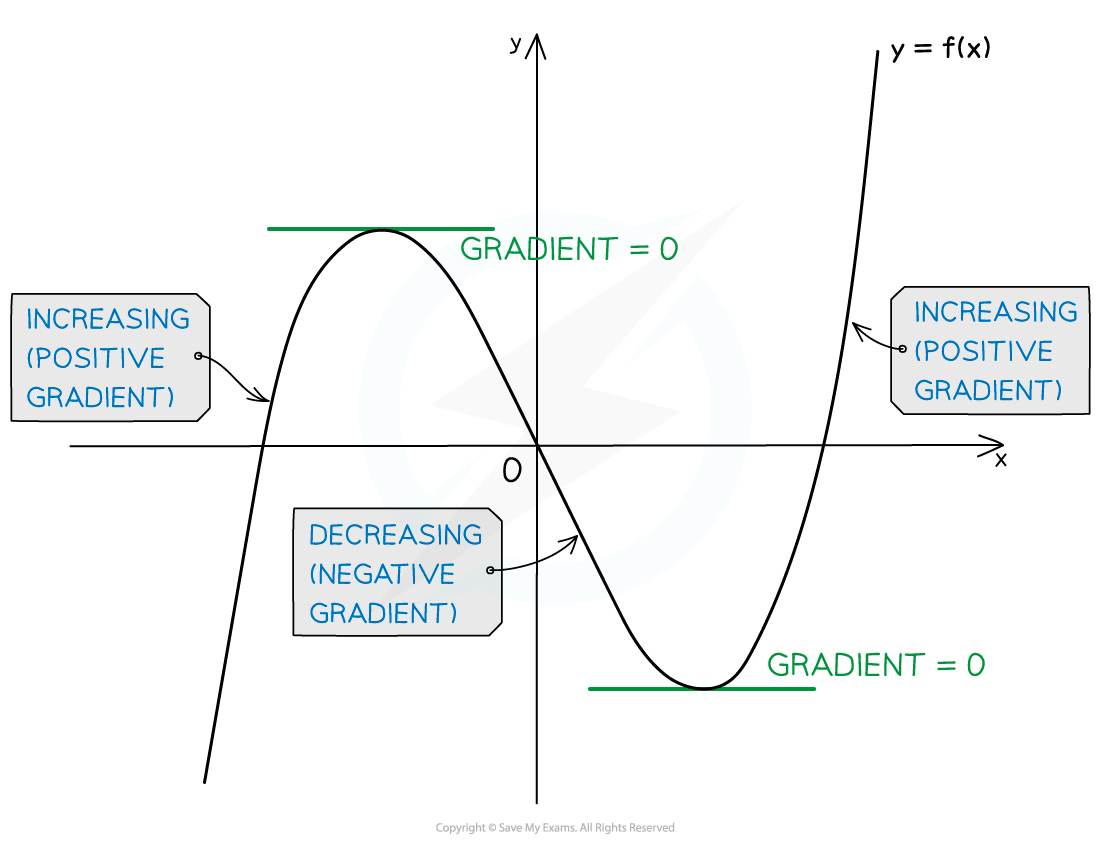
What are increasing and decreasing functions?

• A function,, is increasing if

  • This means the value of the function (‘output’) increases as increases

• A function,, is decreasing if

  • This means the value of the function (‘output’) decreases as increases

• A function,, is stationary where

How do I find where functions are increasing, decreasing or stationary?

• To identify the intervals on which a function is increasing or decreasing 

STEP 1

Find the derivative

STEP 2

Solve the inequalities

 (for increasing intervals) and/or

 (for decreasing intervals)

• Most functions are a combination of increasing intervals, decreasing intervals and stationary points

  • a range of values of (interval) is given where a function satisfies each condition

  • e.g.  The function has derivative so

    •  is decreasing for

    •  is stationary at

    •  is increasing for