Concavity & Points of Inflection (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
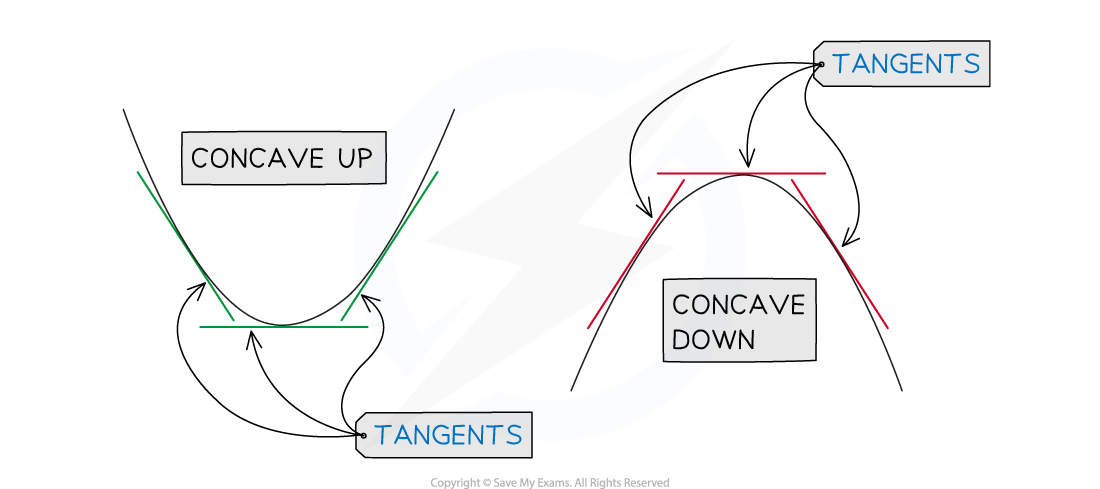
Concavity of a function
What is concavity?
Concavity is the way in which a curve (or surface) 'bends'
Mathematically,
a curve is CONCAVE DOWN if
for all values of
in an interval
a curve is CONCAVE UP if
for all values of
in an interval
Examiner Tips and Tricks
In an exam an easy way to remember the difference is:
Concave down is the shape of (the mouth of) a sad smiley ☹︎
Concave up is the shape of (the mouth of) a happy smiley ☺︎
Worked Example
The function is given by
.
a) Determine whether the curve of the graph of is concave down or concave up at the points where
and
.

b) Find the values of for which the curve of the graph of
is concave up.
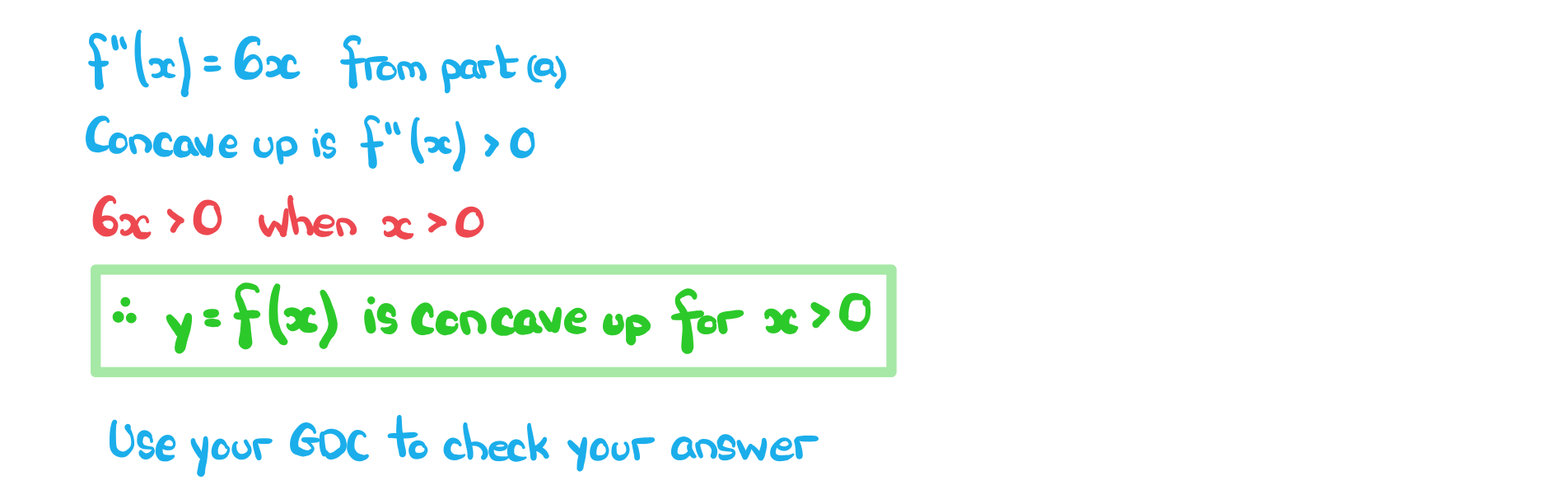
Did this video help you?
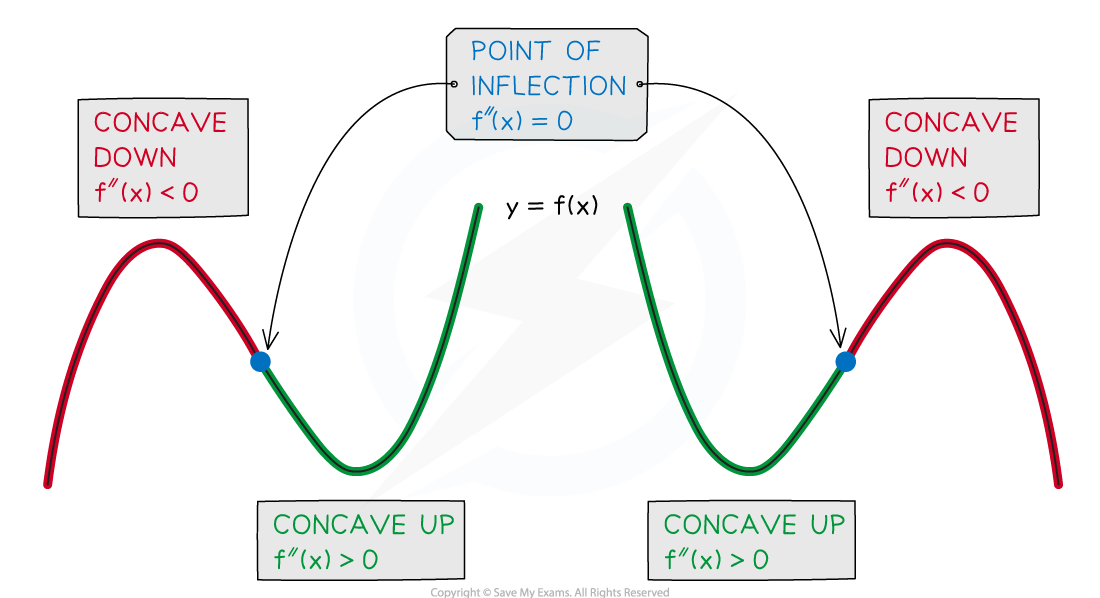
Points of inflection
What is a point of inflection?
A point of inflection is a point at which the graph of
changes concavity
Instead of 'inflection', the alternative spelling inflexion may sometimes be used
What are the conditions for a point of inflection?
A point of inflection requires BOTH of the following two conditions to hold
The second derivative is zero at the point
AND
The graph of
changes concavity at the point
changes sign through a point of inflection
It is important to understand that the first condition is not sufficient on its own to locate a point of inflection
Points where
could be local minimum or maximum points
the first derivative test would be needed
However, if it is already known that
has a point of inflection at some
, say, then
What about the first derivative, like with turning points?
A point of inflection, unlike a turning point, does not necessarily need to have a first derivative value of 0 (i.e.
is not necessarily true)
If it does, it is also a stationary point and is often called a horizontal point of inflection
The tangent to the curve at this point would be horizontal
The normal distribution is an example of a commonly used function that has a graph with two non-stationary points of inflection
How do I find the coordinates of a point of inflection?
For the function
STEP 1
Differentiate
twice to find
, and solve
to find the
-coordinates of possible points of inflection
STEP 2
Use the second derivative to test the concavity of
either side of
If
then
is concave down
If
then
is concave up
If the concavity changes at
, then
is a point of inflection
STEP 3
If required, the
-coordinate of a point of inflection can be found by substituting the
-coordinate into
Examiner Tips and Tricks
You can find the x-coordinates of the point of inflections of by drawing the graph of
and finding the x-coordinates of any local maximum or local minimum points.
Another way is to draw the graph of and find the x-coordinates of the points where the graph crosses (not just touches) the x-axis.
Worked Example
Find the coordinates of the point of inflection on the graph of.
Fully justify that your answer is a point of inflection.


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?