Negative Integrals (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Negative integrals
What do we mean by 'negative integrals'?
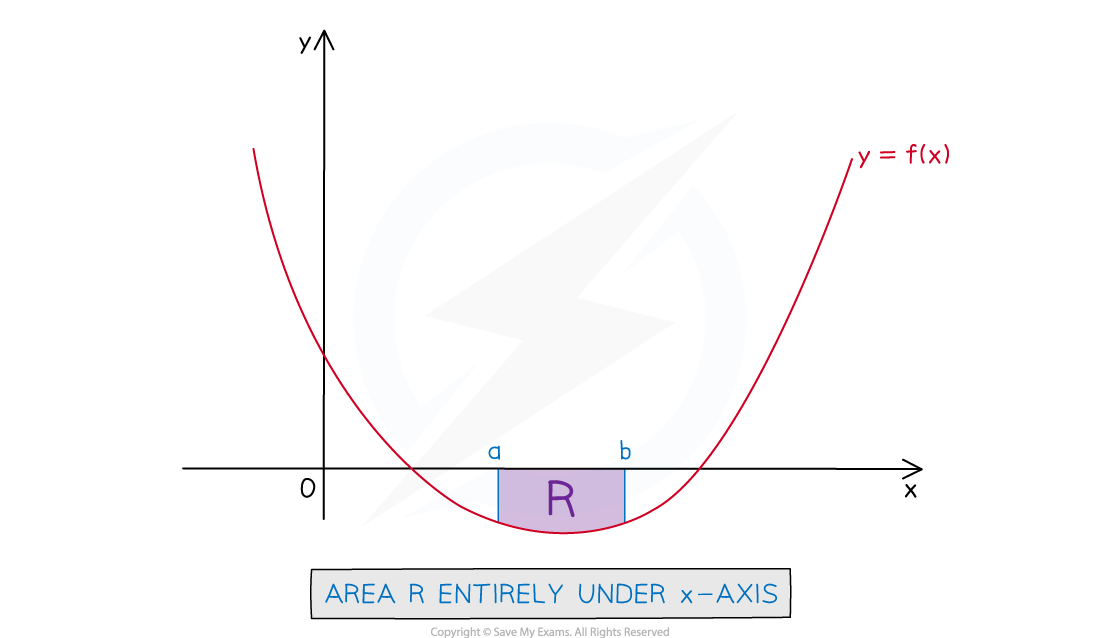
The area between a curve and the
-axis may appear fully or partially under the
-axis
This occurs when the function
takes negative values within the boundaries of the area
The definite integrals used to find such areas will be
negative if the area is fully under the
-axis
possibly negative if the area is partially under the
-axis
In neither case will the integral give you the (positive) answer you are looking for for the area
How do I find the area under a curve when the curve is fully under the x-axis?
STEP 1
Write the expression for the definite integral to find the area as usual
This may involve finding the lower and upper limits from a graph sketch or GDC and f(x) may need to be rewritten in an integrable form
STEP 2
The answer to the definite integral will be negative
Area must always be positive so take the modulus (absolute value) of it
e.g. If
then the area would be 36 (square units)
How do I find the area under a curve when some of the curve is below the x-axis?
Use the modulus function
The modulus is also called the absolute value (Abs)
Essentially the modulus function makes all function values positive
Graphically, this means any negative areas are reflected in the
-axis

A GDC will recognise the modulus function
look for a key or on-screen icon that says 'Abs' (absolute value)
Examiner Tips and Tricks
This modulus version of the integral area formula is given in the formula booklet.
Note that it will also work to find an area that is fully under the -axis.
STEP 1
If a diagram is not given, use a GDC to draw the graph of
If not identifiable from the question, use the graph to find the limits
and
STEP 2
Write down the definite integral needed to find the required area
Remember to include the modulus ( | ... | ) symbols around the function
Use the GDC to evaluate the integral
Examiner Tips and Tricks
If a diagram is not provided, sketching one can really help in this sort of question. Your GDC can help with this.
You can also apply ‘
’ manually, by splitting the integral into positive and negative parts
Write an integral and evaluate each part separately
Change any negative values found to positive
Then add all the positive values together to give the total area
Worked Example
The diagram below shows the graph of where
.
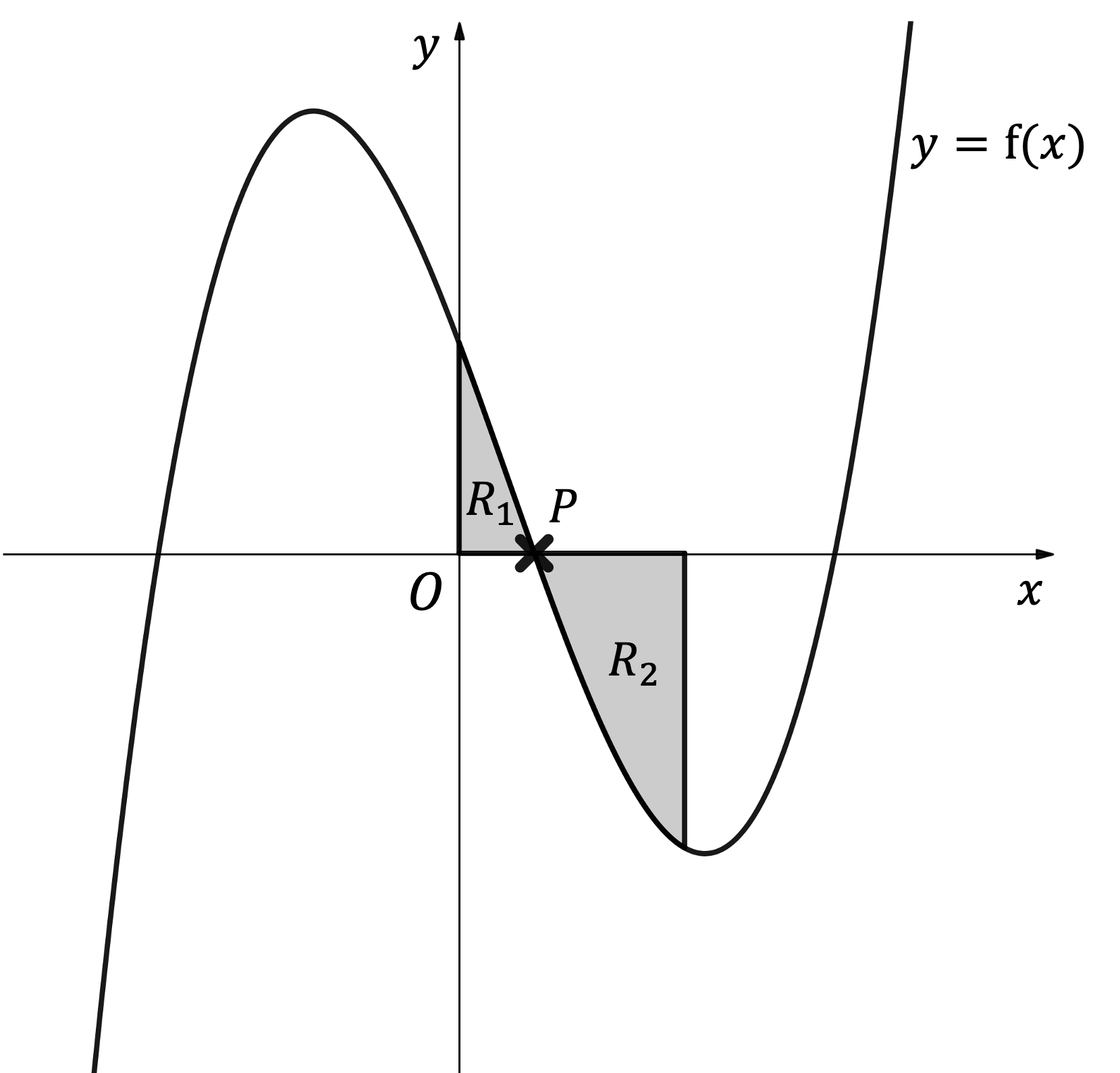
The region is bounded by the curve
, the
-axis and the
-axis.
The region is bounded by the curve
, the x-axis and the line
.
Find the total area of the shaded regions, and
.


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?