Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)HLRevision Notes2. FunctionsFunctions ToolkitPeriodic Functions

Periodic Functions (DP IB Analysis & Approaches (AA)): Revision Note

Dan Finlay

Written by: Dan Finlay

Reviewed by: Mark Curtis

Updated on

DP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): HL

Periodic functions

What are periodic functions?

  • A function f left parenthesis x right parenthesis is called periodic, with period k, if

    • space f left parenthesis x plus k right parenthesis equals f left parenthesis x right parenthesis for all values of x

  • Examples of periodic functions include

    • sin space x and cos space x with period 2 pi (360°)

    • tan space x with period pi (180°)

    • Linear combinations of periodic functions with the same period

      • For example: f open parentheses x close parentheses equals 2 sin invisible function application open parentheses 3 x close parentheses minus 5 cos invisible function application open parentheses 3 x plus 2 close parentheses

What do graphs of periodic functions look like?

  • The graph of a periodic function has translational symmetry

    • The graph is unchanged by translations that are integer multiples of stretchy left parenthesis table row k row 0 end table stretchy right parenthesis

    • The means that the graph appears to repeat the same section (cycle) infinitely

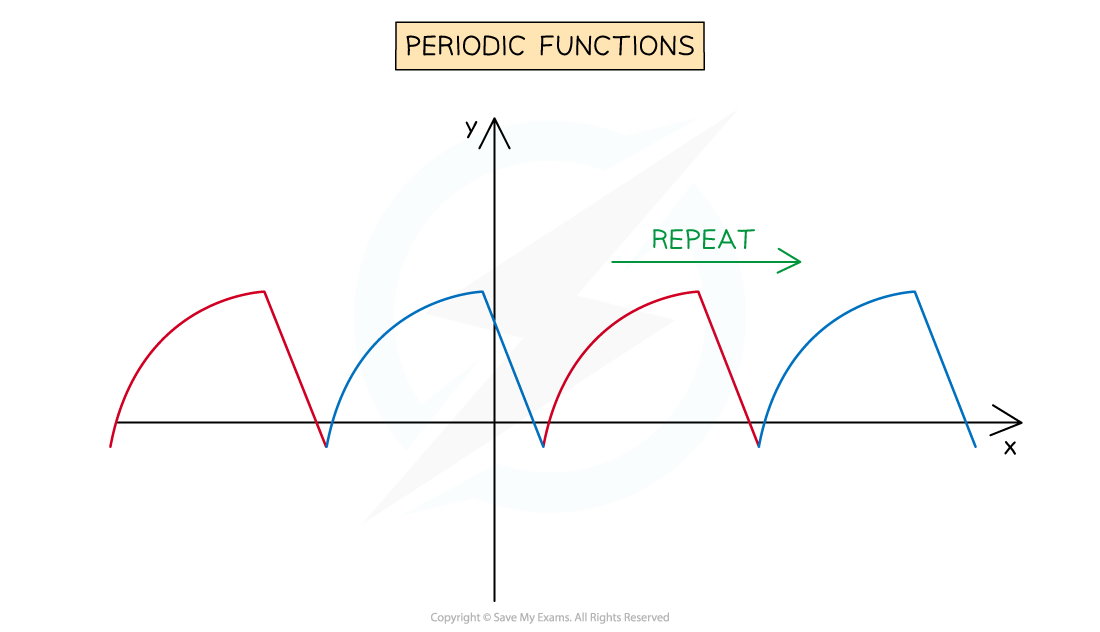
Graph of periodic functions with x and y axes, showing how the graph repeats itself infinitely.

  • Periodic graphs can have infinitely many points of intersection with other graphs

    • e.g. the graph of y equals tan space x and the horizontal line y equals square root of 3 intersect

      • at x equals 60 degree comma space 240 degree comma space 420 degree comma space... and at x equals negative 120 degree comma negative 300 degree comma space...

      • i.e. x equals 60 degree plus 180 k degree where k element of straight integer numbers

Worked Example

The graph space y equals f left parenthesis x right parenthesis is shown below. Given that space f is periodic, write down the period.

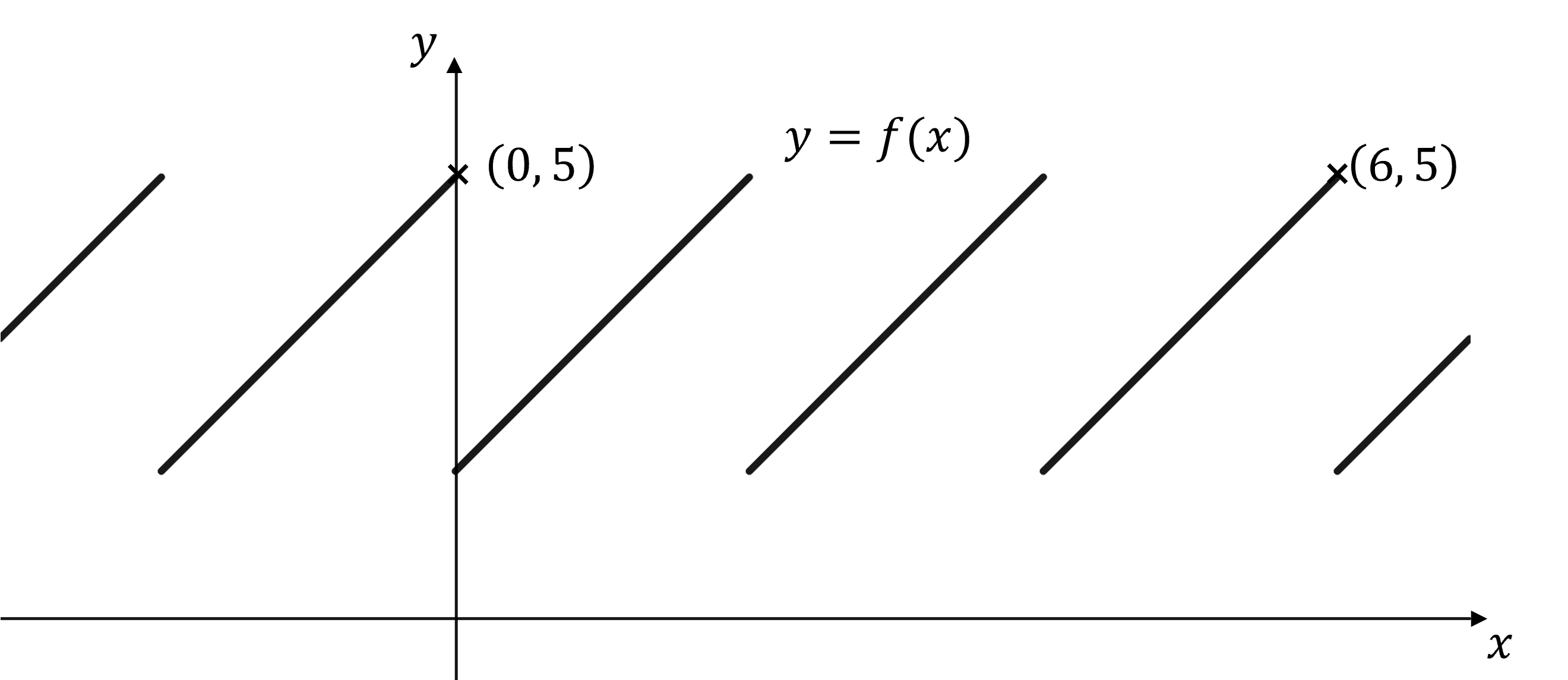
2-3-3-ib-aa--ai-we-image-c
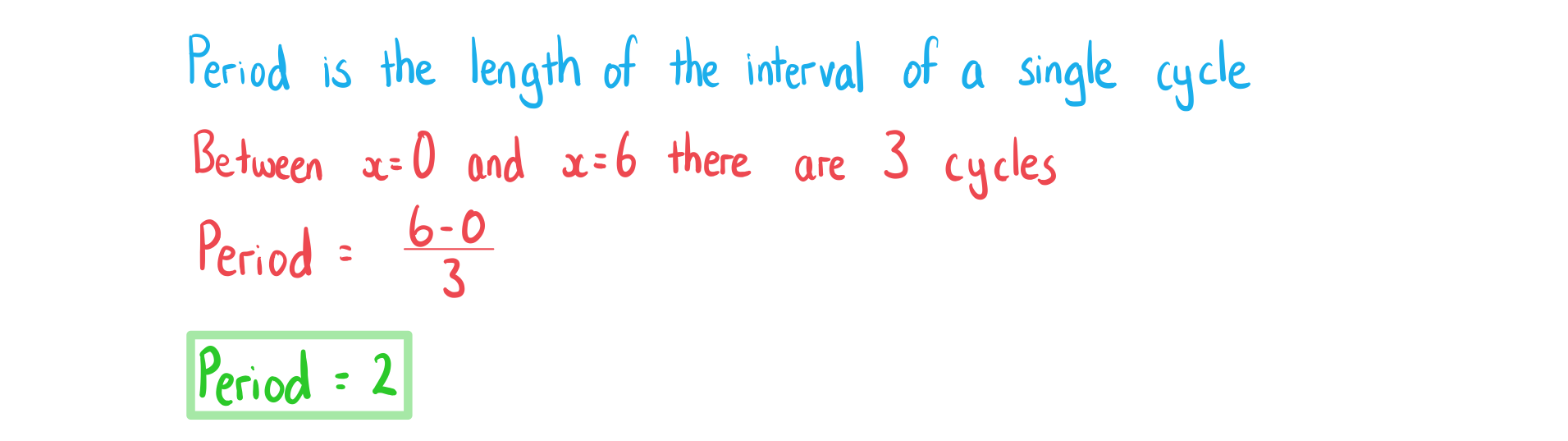
2-3-3-ib-aa-hl-periodic-functions-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Odd & Even FunctionsNext:Self-Inverse Functions
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Mark Curtis

    Reviewer: Mark Curtis

    Expertise: Maths Content Creator

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.