IBMathsDPAnalysis & Approaches (AA)HLRevision Notes3. Geometry & TrigonometryVector Equations of LinesAngle Between Two Lines

Angle Between Two Lines (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

DP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): HL

Did this video help you?

Angle between two lines

How do we find the angles between two lines?

  • The angles between two lines are equal to the angles between their direction vectors

    • They can be found using the scalar product of their direction vectors

  • The intersection of two lines will always create two pairs of equal angles

    • one pair are acute

    • the other are obtuse

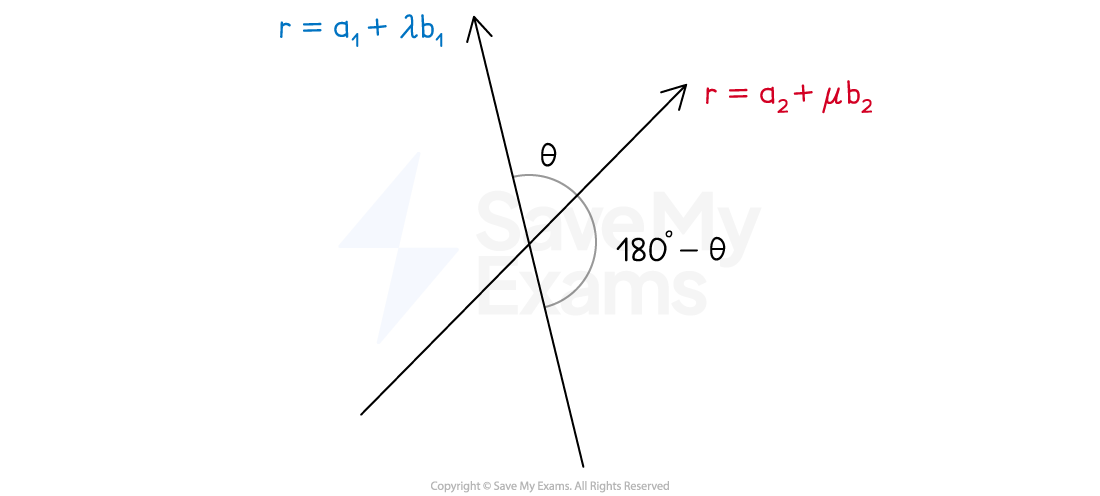
Intersecting lines with angles theta and 180 minus theta, labelled as r equals a1 plus lambda b1 and r equals a2 plus mu b2 in blue and red text.
Angles between two lines

  • You can find one angle between bold italic r equals bold italic a subscript 1 plus lambda bold italic b subscript 1 and bold italic r equals bold italic a subscript 2 plus lambda bold italic b subscript 2 using theta equals cos to the power of negative 1 end exponent open parentheses fraction numerator bold italic b subscript 1 blank bold times blank bold italic b subscript 2 over denominator open vertical bar bold italic b subscript 1 close vertical bar open vertical bar blank bold italic b subscript 2 close vertical bar end fraction close parentheses

  • You can find the other angle by subtracting this from 180°

    • Or from pi if you are working in radians

  • The sign of the scalar product determines whether theta is acute or obtuse

    • It is acute if the scalar product is positive

    • It is obtuse if the scalar product is negative

  • You can always find the acute angle first by taking the absolute value of the scalar product

    •  cos to the power of negative 1 end exponent open parentheses fraction numerator open vertical bar bold italic b subscript bold 1 blank times blank bold b subscript bold 2 close vertical bar over denominator open vertical bar bold italic b subscript 1 close vertical bar open vertical bar blank bold italic b subscript 2 close vertical bar end fraction close parentheses

Worked Example

Find the acute angle, in radians between the two lines defined by the equations:

l subscript 1 colon space space bold italic r equals open parentheses table row 2 row 0 row cell blank 3 blank end cell end table close parentheses plus lambda open parentheses table row 1 row cell negative 4 end cell row cell blank minus 3 blank end cell end table close parentheses and  l subscript 2 colon space space bold italic r equals open parentheses table row 1 row cell negative 4 end cell row 3 end table close parentheses plus mu open parentheses table row cell blank minus 3 blank end cell row 2 row 5 end table close parentheses

R_UZJlZ8_3-10-3-ib-aa-hl-angle-between-we-solution-2a

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourself

Did this page help you?

Previous:Coincident, Parallel, Intersecting & Skew LinesNext:Shortest Distance Between a Point and a Line
Author
Reviewer
Amber

Author: Amber

Expertise: Maths Content Creator

Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Subject Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Angle Between Two Lines