Solving Trigonometric Equations (Cambridge (CIE) IGCSE Additional Maths): Revision Note
Exam code: 606
Did this video help you?
Linear trig equations
How are trigonometric equations solved?
Trigonometric equations can have an infinite number of solutions
For an equation in sin or cos you can add 360° or 2π to each solution to find more solutions
For an equation in tan you can add 180° or π to each solution
When solving a trigonometric equation you will be given a range of values within which you should find all the values
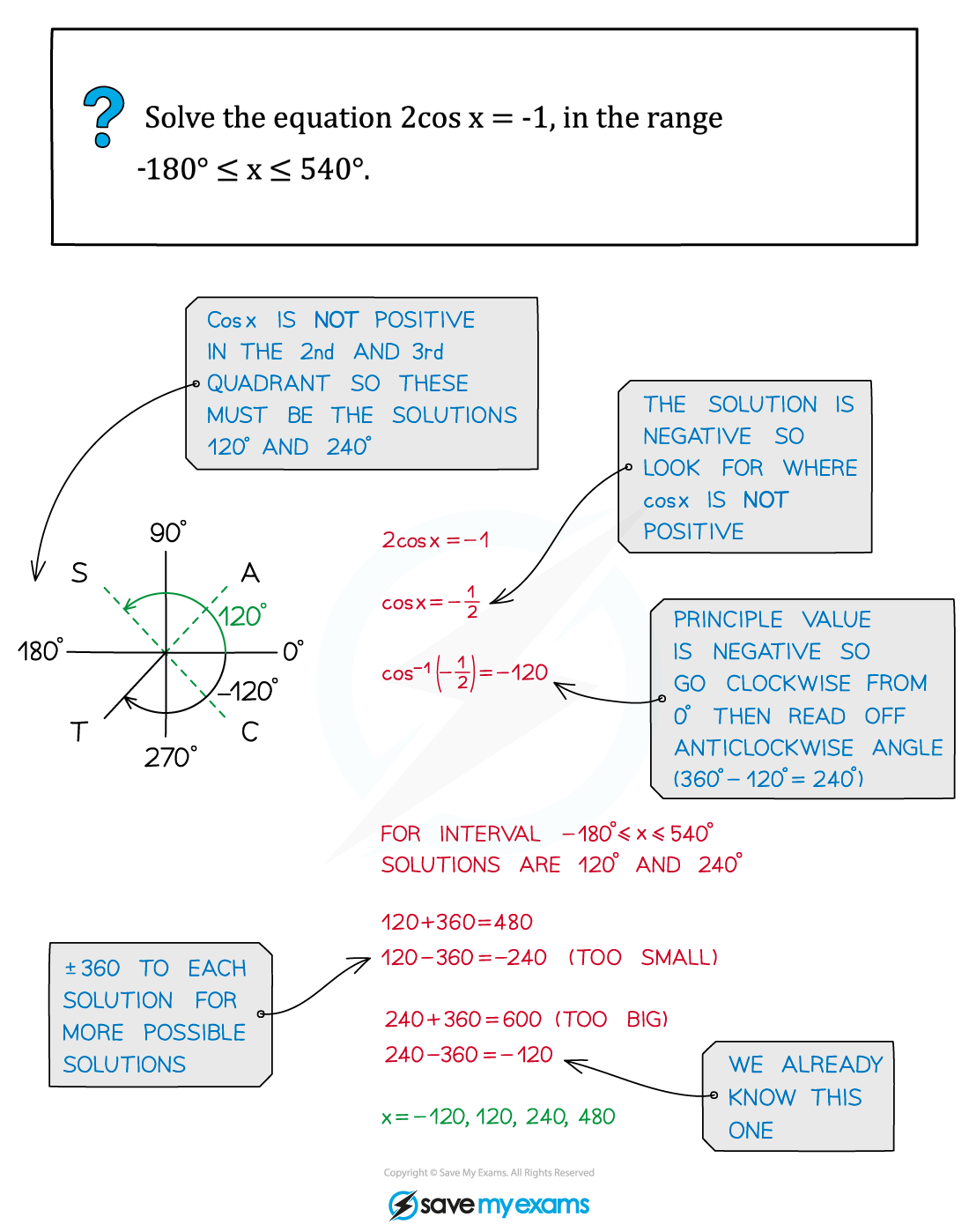
Solving the equation normally and using the inverse function on your calculator or your knowledge of exact values will give you the primary value
The secondary values can be found with the help of:
The unit circle
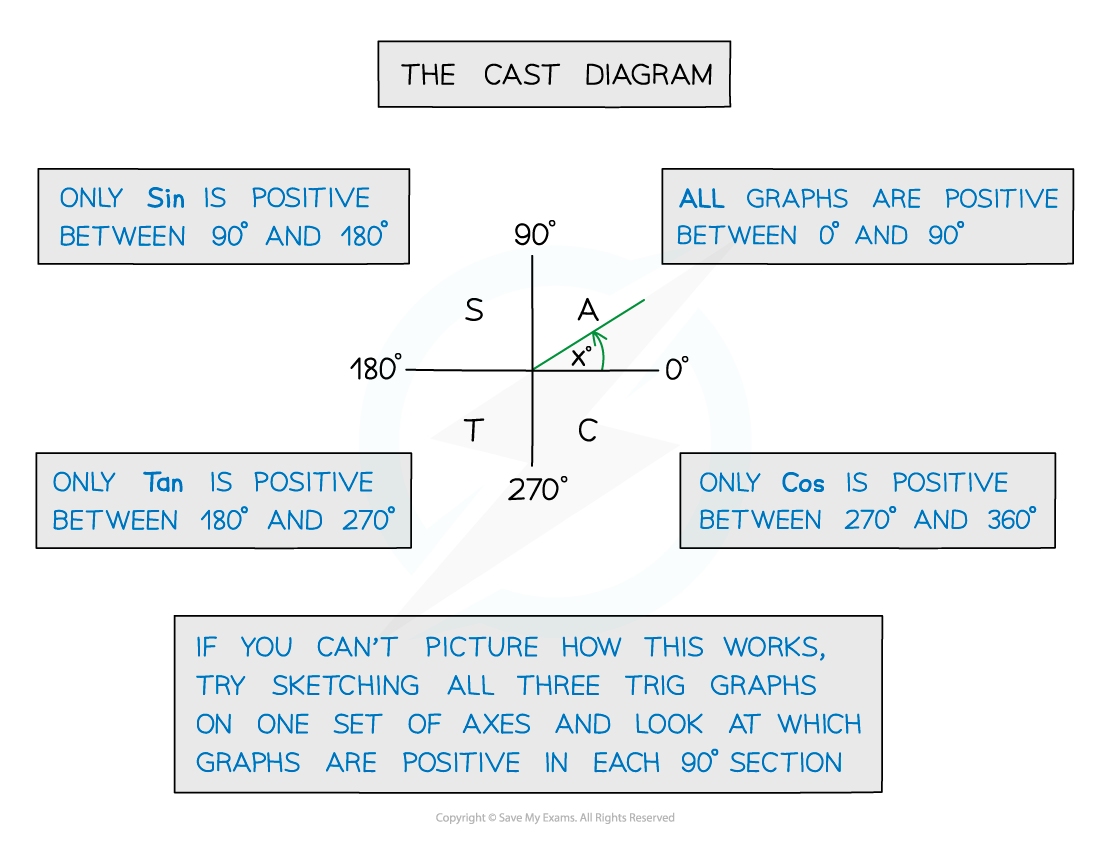
By using the CAST diagram which shows where each function has positive solutions
The graphs of trigonometric functions
By sketching the graph (see Graphs of Trigonometric Functions) you can read off all the solutions in a given range (or interval)
By using trigonometric identities you can simplify harder equations
You may be asked to use degrees or radians to solve trigonometric equations
Make sure your calculator is in the correct mode
Remember common angles
90° is ½π radians
180° is π radians
270° is 3π/2 radians
360° is 2π radians
How are trigonometric equations of the form sin x = k solved?
It is a good idea to sketch the graph of the trigonometric function first
Use the given range of values as the domain for your graph
The intersections of the graph of the function and the line y = k will show you
The location of the solutions
The number of solutions
You will be able to use the symmetry properties of the graph to find all secondary values within the given range of values
The method for finding secondary values are:
For the equation sin x = k the primary value is x1 = sin -1 k
A secondary value is x2 = 180° - sin -1 k
Then all values within the range can be found using x1 ± 360n and x2 ± 360n where n ∈
For the equation cos x = k the primary value is x1 = cos -1 k
A secondary value is x2 = - cos -1 k
Then all values within the range can be found using x1 ± 360n and x2 ± 360n where n ∈
For the equation tan x = k the primary value is x = tan -1 k
All secondary values within the range can be found using x ± 180n where n ∈
How do I use the CAST diagram?

What about more complicated trig equations?
Some trig equations could involve a function of x or θ (see Transformations of Trigonometric Functions)
Trigonometric equations in the form sin(ax + b) can be solved in more than one way
The easiest method is to consider the transformation of the angle as a substitution
For example let u = ax + b
Transform the given interval for the solutions in the same way as the angle
For example if the given interval is 0° ≤ x ≤ 360° the new interval will be
(a (0°) + b) ≤ u ≤ (a (360°) + b)
Solve the function to find the primary value for u
Use either the unit circle or sketch the graph to find all the other solutions in the range for u
Undo the substitution to convert all of the solutions back into the corresponding solutions for x
Another method would be to sketch the transformation of the function
If you use this method then you will not need to use a substitution for the range of values

What about equations using sec, cosec, and cot?
Equations in the form
(or
or
) are not solvable using your calculator, as it does not have an inverse function for these
Use the definitions of these functions to rewrite the equation in terms of
,
, or
and then solve as normal, remembering to find all the solutions within the given domain of
It is often useful to swap sec, cosec, and cot for their definitions as one of the first steps when solving an equation
Examiner Tips and Tricks
Your calculator will only give you the principal value and you need to find all other solutions for the given interval
Also, remember the CAST diagram only gives you some solutions, so again you may need to find more depending on the given interval
It is entirely up to you how you solve a trig equation, but some ways are more helpful than others depending on the type of equation you are trying to solve
Worked Example
Did this video help you?
Quadratic trig equations
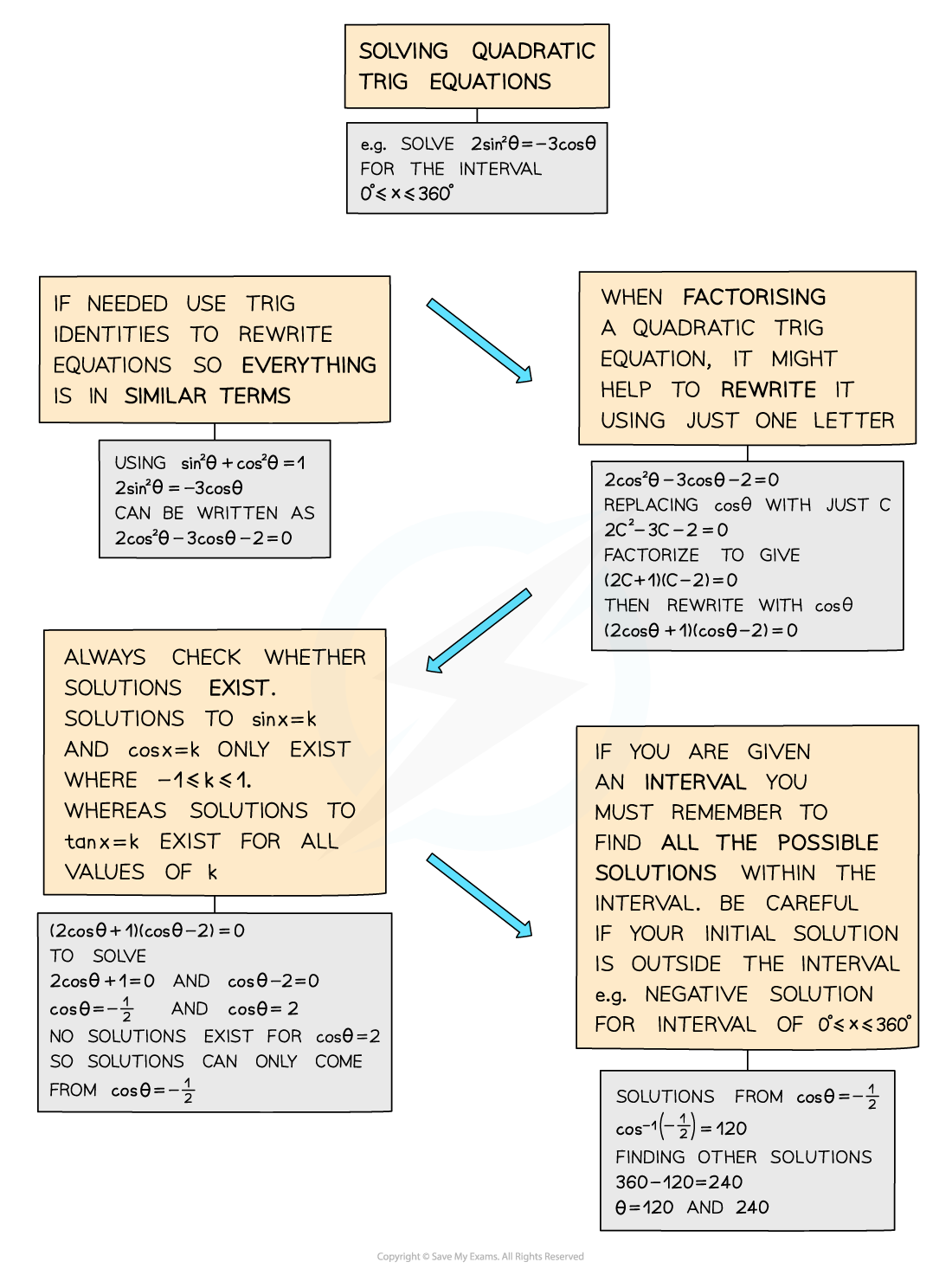
How are quadratic trigonometric equations solved?
A quadratic trigonometric equation is one that includes either
,
or
Often the identity
can be used to rearrange the equation into a form that is possible to solve
If the equation involves both sine and cosine then the Pythagorean identity should be used to write the equation in terms of just one of these functions
If the equation involves a mixture of regular trig functions (sin, cos, and tan) as well as reciprocal functions (sec, cosec, and cot) it may be useful to:
rewrite the reciprocal trig functions using their definitions,
use the identities
and
Solve the quadratic equation using the quadratic equation or factorisation
This can be made easier by changing the function to a single letter
Such as changing
to
A quadratic can give up to two solutions
You must consider both solutions to see whether a real value exists
Remember that solutions for sin θ = k and cos θ = k only exist for -1 ≤ k ≤ 1
Solutions for tan θ = k exist for all values of k
Find all solutions within the given interval
There will often be more than two solutions for one quadratic equation
The best way to check the number of solutions is to sketch the graph of the function
You may be asked to use degrees or radians to solve trigonometric equations
Make sure your calculator is in the correct mode
Remember common angles
90° is ½π radians
180° is π radians
270° is 3π/2 radians
360° is 2π radians
Examiner Tips and Tricks
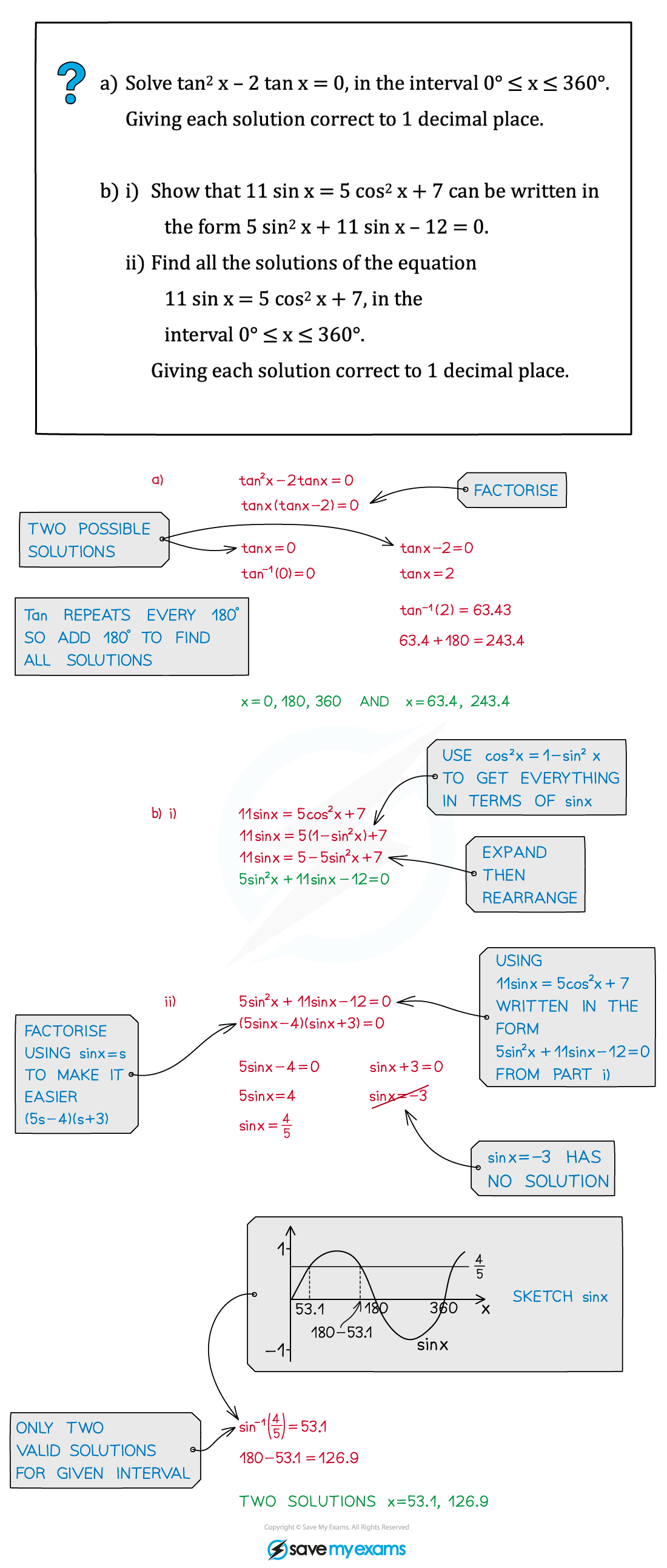
Sketch the appropriate sin, cos, tan graph to ensure you find ALL solutions within the given interval, and be super careful if you get a negative solution but have a positive interval
For example, for an equation, in the interval 0° ≤ x ≤ 360°, with solution sin x = ‑¼ then sin‑1(‑¼) = -14.5 (to 1d.p.), which is not between 0 and 360
by sketching the graph you’ll be able to spot the two solutions will be 180 + 14.5 and 360 ‑ 14.5
Worked Example
Did this video help you?
Strategy for further trig equations
How to approach solving trig equations
You can solve trig equations in a variety of different ways
Sketching a graph (see Graphs of Trig Functions)
Using trigonometric identities (see Simple Trig Identities and Further Trig identities)
Using the CAST diagram (see Linear Trig Equations)
Factorising quadratic trig equations (see Quadratic Trig Equations)
You may be asked to use degrees or radians to solve trigonometric equations
Make sure your calculator is in the correct mode
Remember common angles
90° is ½π radians
180° is π radians
270° is 3π/2 radians
360° is 2π radians
If you’re having trouble solving a trig equation, this flowchart might help:

Examiner Tips and Tricks
Don’t forget to check the function range and ensure you have included all possible solutions
If the question involves a function of x or θ, make sure you transform the range first (and ensure you transform your solutions back again at the end!)
Worked Example


Unlock more, it's free!
Did this page help you?