Half-Life (SQA National 5 Chemistry): Revision Note
Exam code: X813 75
Half-life of isotopes
What is half-life?
Radioactive decay is the process where the nuclei of unstable atoms (radioisotopes) break down to become more stable
Half-life is a measure of how quickly this happens for a particular radioisotope
It is defined as:
"the time taken for half of the nuclei in a sample of a particular isotope to decay"
It is given the symbol, t1/2
Half-life is constant
So, after each half-life, the amount of the radioisotope remaining is halved:
100% 50%
25%
12.5%
6.25%
For example, for 250g of an isotope with a half-life of 30 years:
Number of years | Number of half-lives | Amount of sample (g) |
|---|---|---|
0 | 0 | 250 |
30 | 1 | 125 |
60 | 2 | 62.5 |
90 | 3 | 31.25 |
Half-life is unaffected by conditions
It is a nuclear property
So, it is not changed by:
Physical conditions like temperature or pressure
Chemical conditions, such as the compound that the isotope is part of
Half-life is used for dating
The known, constant half-life of radioisotopes, like carbon-14, can be used by scientists to determine the age of ancient materials and artefacts
Half-life calculations
The two main skills for half-life problems are:
Determining half-life from a decay curve (graph)
Performing calculations with given data
1. Determining half-life from a decay curve
A decay curve is a graph that shows how the mass or activity of a radioisotope decreases over time
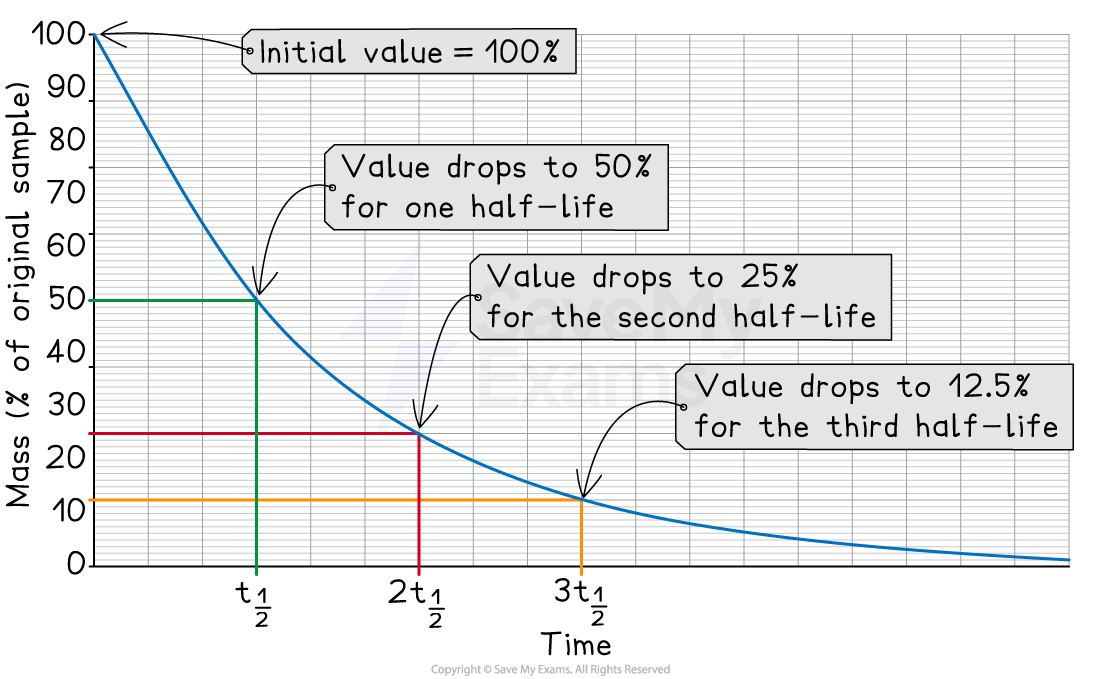
The half-life (t1/2) is the time it takes for the mass or percentage of the sample to fall to half of its original value
After a second half-life, it will have fallen to a quarter of its original value
How to find the half-life from a decay curve:
Read the initial value on the y-axis (at time = 0)
Divide this value by two to find the half-way point
Find this half-way value on the y-axis and draw a line across to the curve
Then, draw another line straight down to the x-axis
Read the time off the x-axis to get the half-life
Worked Example
The radioisotope cobalt-60 is used in medicine. The graph below shows how the cobalt-60 content of a sample varies with time.
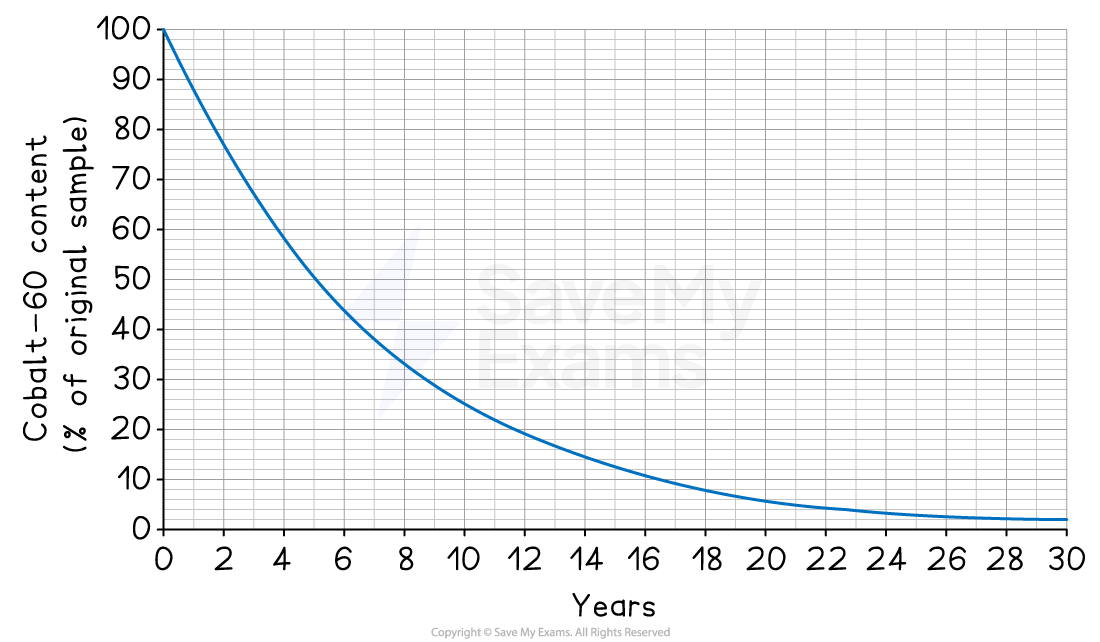
Determine the half-life of cobalt-60.
[1]
Answer:
From the graph, the initial cobalt-60 content is 100%
Half of this is 50%
Find 50% on the y-axis and draw a line across to the curve
Now, draw a line straight down to the x-axis
Read the value off the x-axis to get the half-life
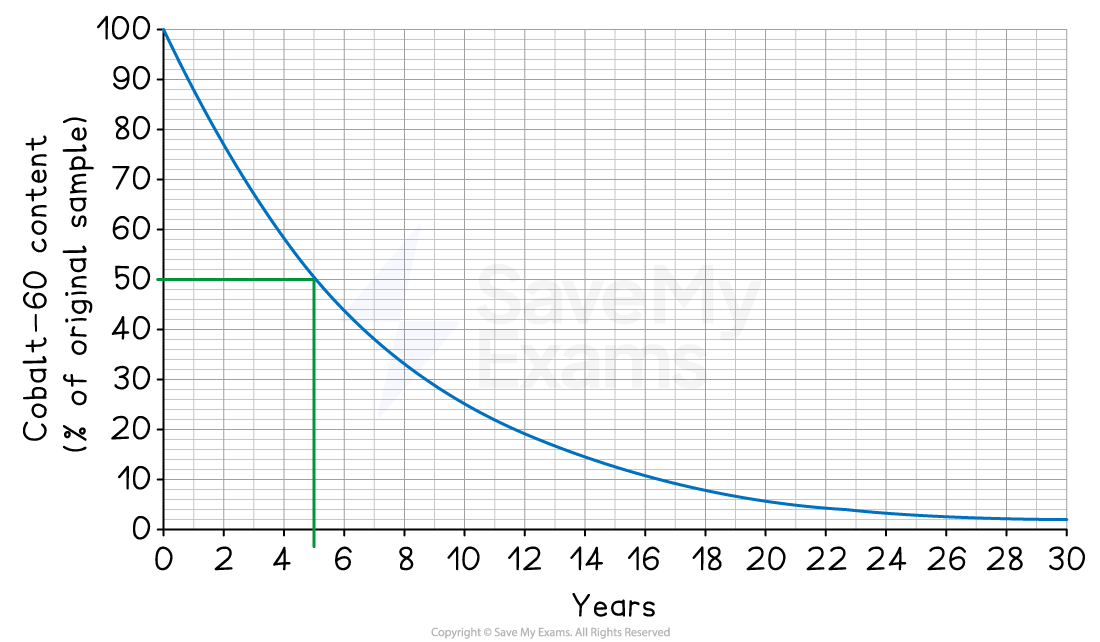
The half-life of cobalt-60 is 5 years [1 mark]
2. Performing half-life calculations
These questions involve the relationship between:
The starting amount
The final amount
The number of half-lives
The total time
The "arrow method"
An easy and reliable way to solve half-life problems is to use the "arrow method"
This method tracks the decay process
Each arrow represents one half-life passing
During this time, the amount of the radioisotope is halved
For example, tracking the decay of an 80g sample
80 g 40 g
20 g
10 g
5 g
By counting the arrows, you can find out how many half-lives have passed to get from the start amount to the end amount
Worked Example
Calculating half-life
A sample of a radioisotope has an initial mass of 80 mg. After 60 hours, its mass has fallen to 5 mg.
Calculate the half-life of the isotope.
[2]
Answer:
Find the number of half-lives using the arrow method:
80mg → 40mg → 20mg → 10mg → 5mg
Count the arrows:
There are 4 arrows, so 4 half-lives have passed [1 mark]
Calculate the duration of one half-life:
half-life =
half-life = = 15 hours [1 mark]
Worked Example
Calculating final amount
A radioisotope has a half-life of 3 days.
If a sample starts with a mass of 120 g, what mass will remain after 9 days?
[2]
Answer:
Find the number of half-lives that will pass:
Number of half-lives = Total Time / Half-life
number of half-lives =
number of half-lives = = 3 half-lives [1 mark]
Use the arrow method to halve the starting amount 3 times:
120 g → 60 g → 30 g → 15 g
So, the final mass remaining is 15 g [1 mark]
Examiner Tips and Tricks
An exam question can try to trick you by asking for the amount that has decayed, instead of the amount that remains
The arrow method always tells you what remains
How to solve these questions:
Always use the arrow method first to find the amount remaining
Then, to find the amount that has decayed, simply subtract the remaining amount from the starting amount
amount decayed = starting amount - amount remaining
Worked Example
A 400g sample of a radioisotope has a half-life of 10 years.
What mass of the isotope has decayed after 30 years?
[2]
Answer:
Find the number of half-lives:
= 3 half-lives [1 mark]
Use the arrow method to find the mass remaining:
400g → 200g → 100g → 50g
So, 50g remains.
Calculate the mass that has decayed:
amount decayed = starting amount - amount remaining
amount decayed = 400g - 50g = 350g [1 mark]

Unlock more, it's free!
Did this page help you?