Modulus Functions (DP IB Analysis & Approaches (AA): HL): Revision Note

Modulus functions & graphs

What is the modulus function?

• The modulus function (or absolute value function) is defined by $f\left(x\right)=\left|x\right|$

  • which gives the positive distance (or size) of a real number $x$ from zero

  • e.g.

    • $\left|3\right|=3$

    • $|-2|=2$

    • $\left|0\right|=0$

• It can also be defined as

  • $\left|x\right|=\{\begin{array}{ll}x& x\ge 0\\ -x& x<0\end{array}$

  • or $\left|x\right|=\sqrt{x^2}$

• Its largest domain is the set of all real values

  • and its range is the set of all real non-negative values

How do I sketch the modulus function?

• The graph of $y=\left|x\right|$ is the line $y=x$ for $x\ge 0$

  • and $y=-x$ for $x<0$

    • giving it a V-shape

    • with its vertex at the origin

• The function is continuous

  • but not differentiable at $x=0$

    • as no gradient exists there

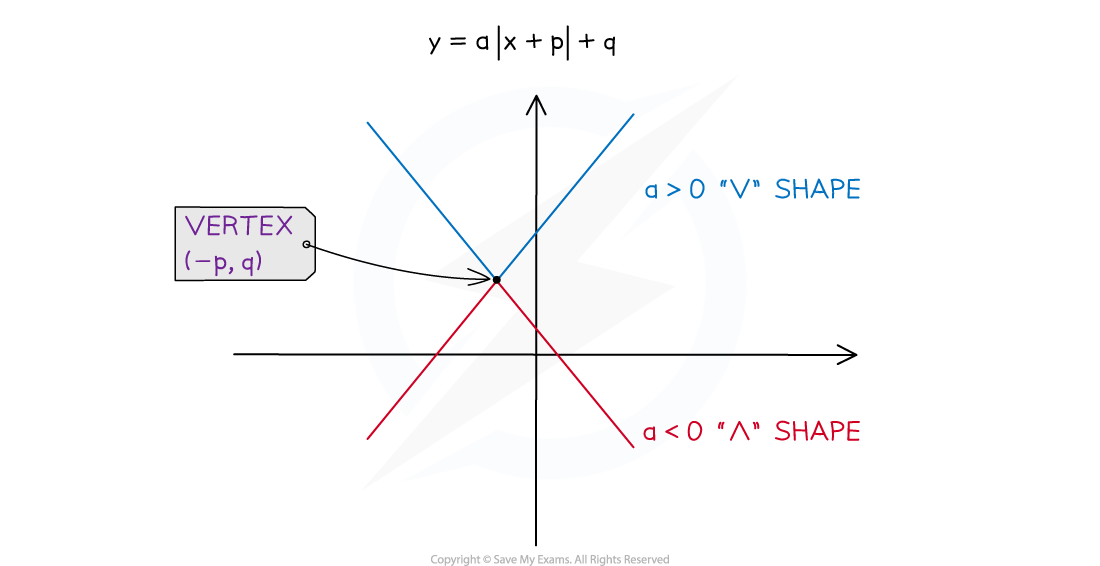
How do I sketch y = a|x + p| + q?

• The graph of $y=a|x+p|+q$ is a transformation of the graph $y=\left|x\right|$ as follows:

  • First, apply a vertical stretch of scale factor $a$ to $y=\left|x\right|$

    • $y=a\left|x\right|$

  • Secondly, apply a translation of $\left(\begin{array}{c}-p\\ q\end{array}\right)$

    • $y=a|x+p|+q$

• This transforms the vertex $\left(0,0\right)$ on $y=\left|x\right|$ to

  • the new vertex at $\left(-p,q\right)$ on $y=a|x+p|+q$

• Note that

  • $a>0$ means a $\vee$ shape

    • the bigger $a$ the steeper the $\vee$

  • $a<0$ means a $\wedge$ shape

    • the more negative the $a$ the steeper the $\wedge$

How do I rearrange a graph into the form y = a|x + p| + q?

• Two useful modulus relations for rearranging are

  • $\left|ab\right|=\left|a\right|\left|b\right|$

  • $\left|a-b\right|=\left|b-a\right|$

• e.g. $y=|6-2x|+1$ can be rearranged as follows:

  • $y=|2x-6|+1$

    • using $\left|a-b\right|=\left|b-a\right|$

  • $y=\left|2\left(x-3\right)\right|+1$

    • by factorisation

  • $y=\left|2\right|\left|\left(x-3\right)\right|+1$

    • using $\left|ab\right|=\left|a\right|\left|b\right|$

  • $\left|2\right|=2$ and $\left|\left(x-3\right)\right|=|x-3|$ giving

    • $y=2|x-3|+1$