IBMathsDPAnalysis & Approaches (AA)HLRevision Notes2. FunctionsQuadratic Functions & GraphsSolving Quadratics

Solving Quadratics (DP IB Analysis & Approaches (AA)) : Revision Note

Dan Finlay

Last updated

DP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): SL

Did this video help you?

Solving Quadratic Equations

How do I decide the best method to solve a quadratic equation?

  • A quadratic equation is of the form a x squared plus b x plus c equals 0

  • If it is a calculator paper then use your GDC to solve the quadratic

  • If it is a non-calculator paper then...

    • you can always use the quadratic formula

    • you can factorise if it can be factorised with integers

    • you can always complete the square

How do I solve a quadratic equation by the quadratic formula?

  • If necessary rewrite in the form a x squared plus b x plus c equals 0

  • Clearly identify the values of a, b & c

  • Substitute the values into the formula

    • x equals fraction numerator negative b plus-or-minus square root of b squared minus 4 a c end root over denominator 2 a end fraction 

      • This is given in the formula booklet

  • Simplify the solutions as much as possible

How do I solve a quadratic equation by factorising?

  • Factorise to rewrite the quadratic equation in the form a left parenthesis x minus p right parenthesis left parenthesis x minus q right parenthesis equals 0

  • Set each factor to zero and solve

    • x minus p equals 0 rightwards double arrow x equals p

    • x minus q equals 0 rightwards double arrow x equals q

How do I solve a quadratic equation by completing the square?

  • Complete the square to rewrite the quadratic equation in the form a open parentheses x minus h close parentheses squared plus k equals 0

  • Get the squared term by itself

    • open parentheses x minus h close parentheses squared equals negative k over a

  • If open parentheses negative k over a close parentheses is negative then there will be no solutions

  • If open parentheses negative k over a close parentheses is positive then there will be two values for x minus h

    • x minus h equals plus-or-minus square root of negative k over a end root

  • Solve for x

    • x equals h plus-or-minus square root of negative k over a end root

Examiner Tips and Tricks

  • When using the quadratic formula with awkward values or fractions you may find it easier to deal with the " b squared minus 4 a c " (discriminant) first

    • This can help avoid numerical and negative errors, improving accuracy

Worked Example

Solve the equations:

a) 4 x squared plus 4 x minus 15 equals 0.

2-2-3-ib-aa-sl-quadratic-equations-a-we-solution

b) 3 x squared plus 12 x minus 5 equals 0.

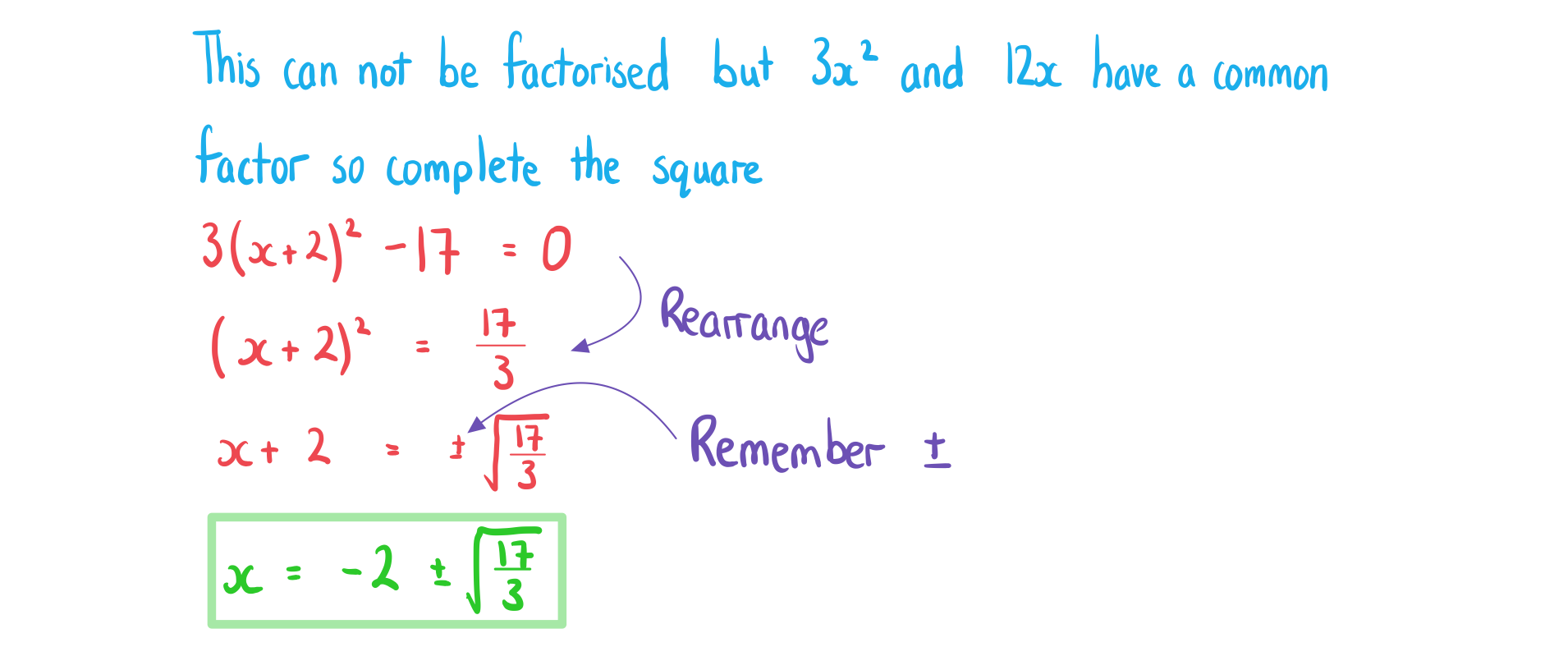
2-2-3-ib-aa-sl-quadratic-equations-b-we-solution

c) 7 minus 3 x minus 5 x squared equals 0.

2-2-3-ib-aa-sl-quadratic-equations-c-we-solution

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourselfFlashcards

Did this page help you?

Previous:Factorising & Completing the SquareNext:Quadratic Inequalities
Dan Finlay

Author: Dan Finlay

Expertise: Maths Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Solving Quadratics