Laws of Logarithms (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
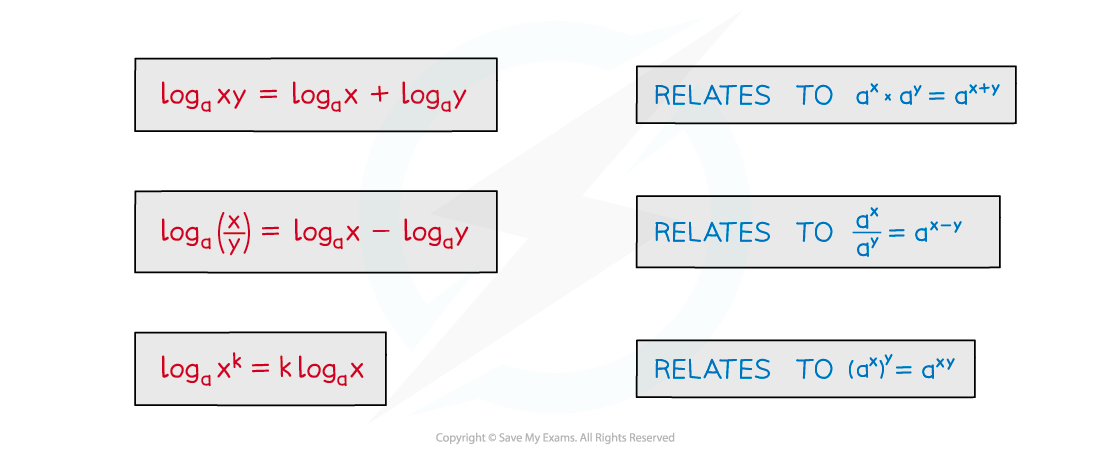
Laws of logarithms
What are the laws of logarithms?
The laws of logarithms (log laws) you need to know are:
These hold for
Examiner Tips and Tricks
The laws of logarithms are given in the formula booklet.
Useful results from the laws of logarithms
This is equivalent to
This is equivalent to
because
because logarithms and powers are inverses
because
Examiner Tips and Tricks
These useful results from log laws are not in the formula booklet.
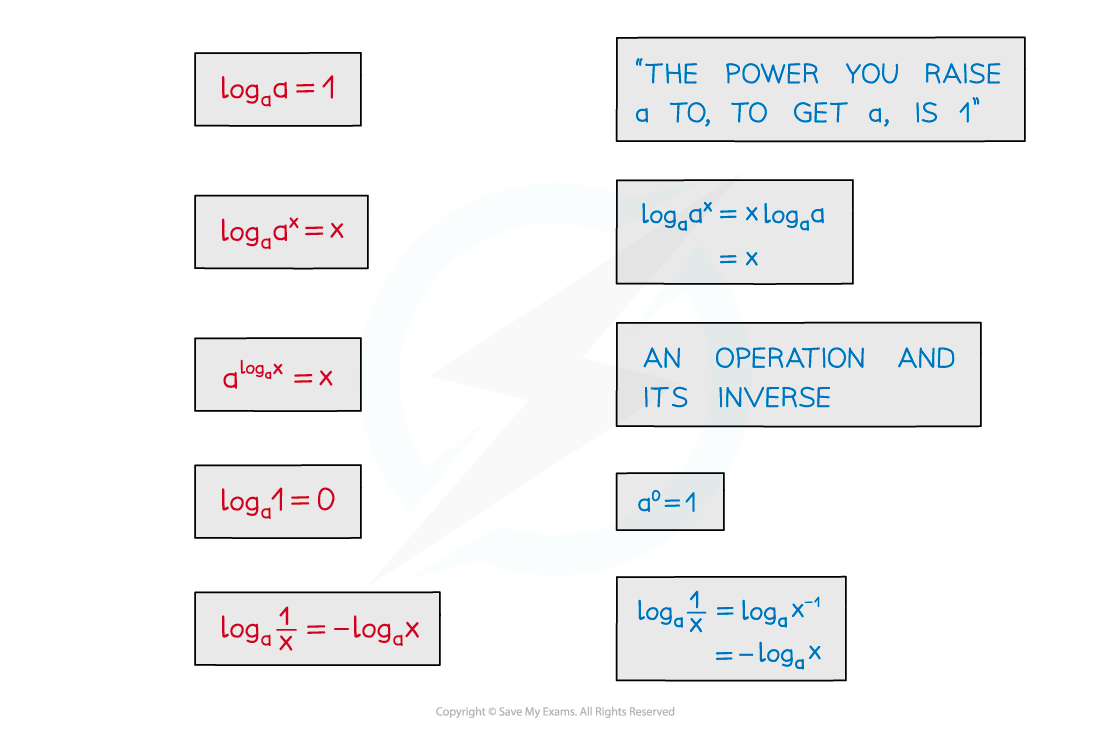
The useful results can be applied to
too
Two particularly useful results are
Examiner Tips and Tricks
Beware:
When are logarithms undefined?
You cannot take the log of zero or the log of a negative number
is defined for
is undefined for
Similarly
is defined for
is undefined for
etc
Examiner Tips and Tricks
When solving an equation involving logs, get rid of any solutions that make the original equation undefined.
Worked Example
a) Write the expression in the form
, where
.
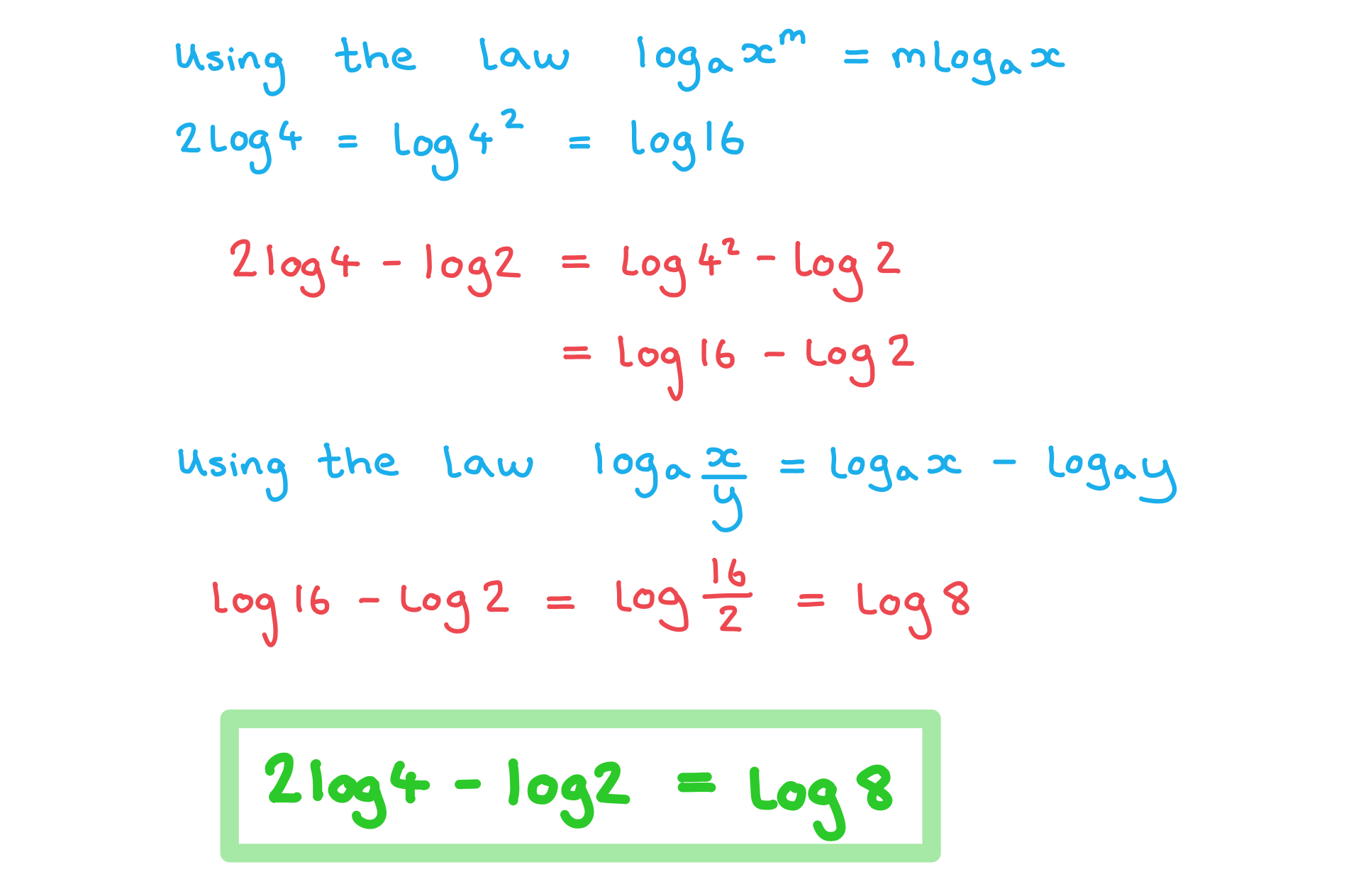
b) Hence, or otherwise, solve .
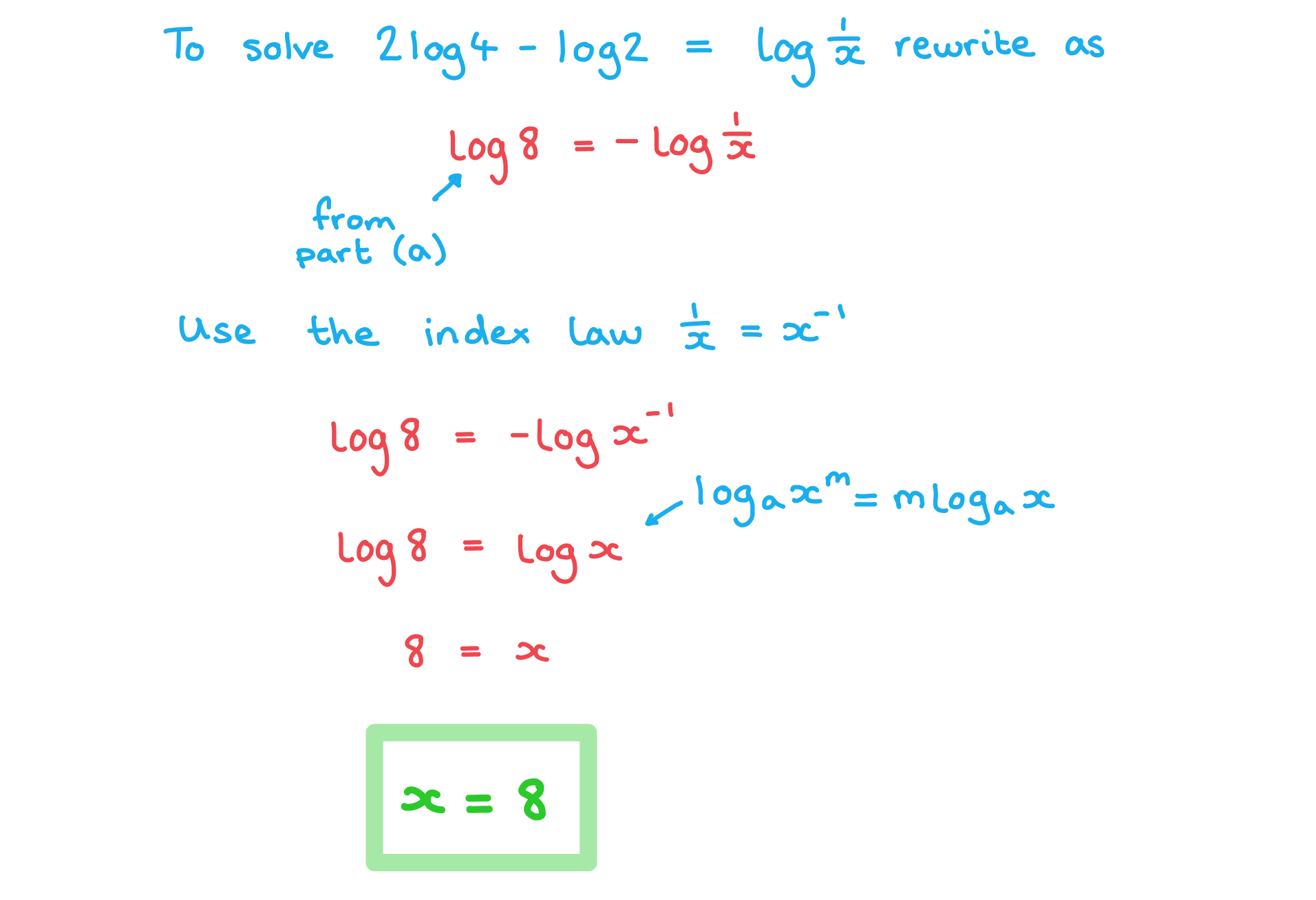
Did this video help you?
Change of base
How do I change the base of a logarithm?
The formula for changing the base of a logarithm is
This allows you to change logarithms into a more useful base
which is helpful in non-calculator questions
Examiner Tips and Tricks
The formula for changing the base of a logarithm is given in the formula booklet.
Worked Example
By choosing a suitable value for , use
to find the value of
without using a calculator.
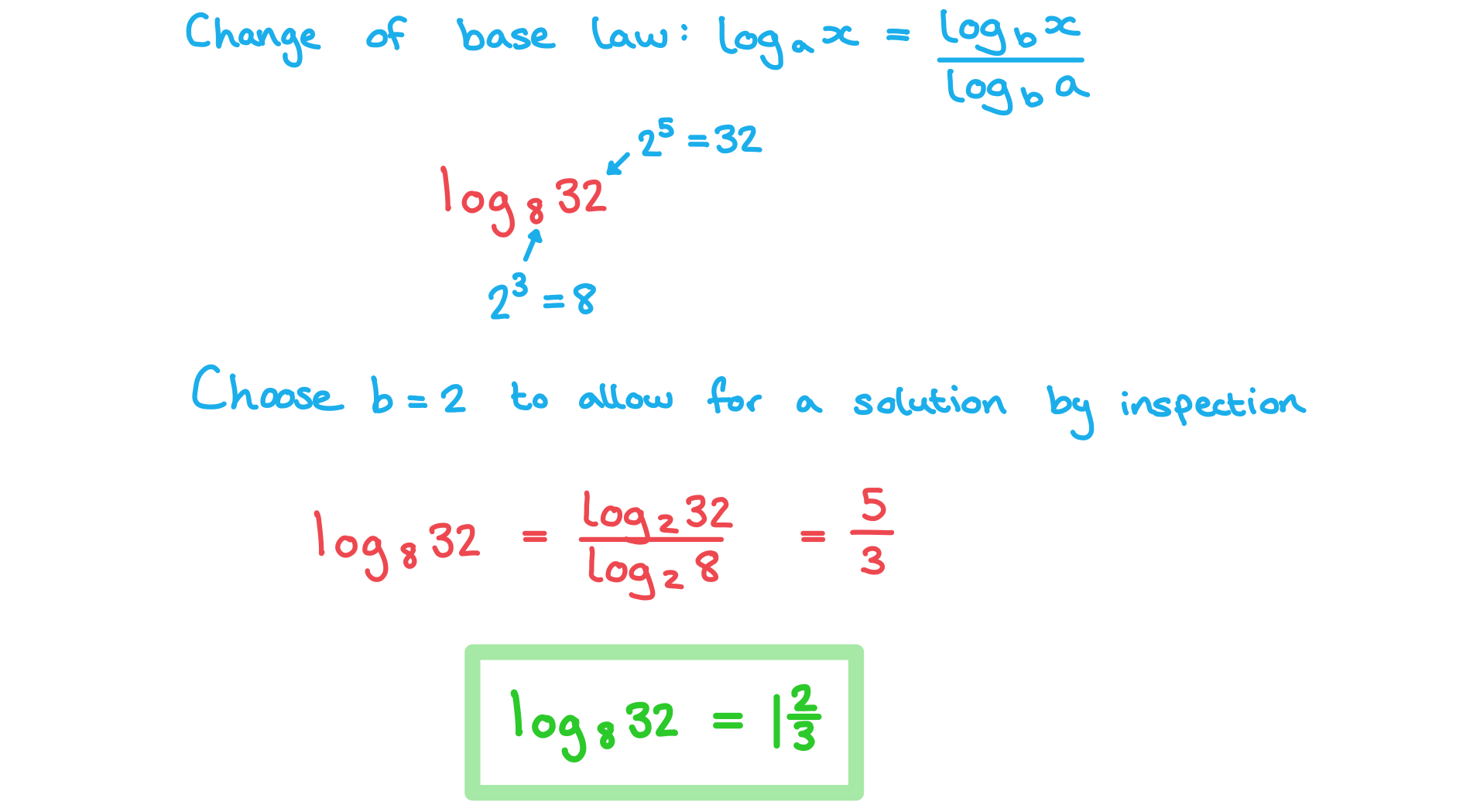

Unlock more, it's free!
Did this page help you?