Line of Symmetry - GCSE Maths Definition

Definition

A line of symmetry is a line that can be drawn on (inside) a (2D) shape such that reflecting the shape along that line would result in the shape looking exactly the same.

Explanation

A line of symmetry ‘splits a shape in half’ - but in a particular way.

As well as splitting the shape in half, a line of symmetry is a mirror line that when each half is reflected in it - i.e. there is a two-way reflection - the original shape appears unchanged.

If a shape is folded along one of its lines of symmetry, the two halves would fit exactly on top of each other; the two identical halves would align exactly.

Lines of symmetry are usually indicated on shapes by a dotted line.

Using the correct terminology of reflections (or more generally, transformations), a shape would be called an ‘object’ and the reflected (transformed) shape would be called the ‘image’. In the two-way reflection explanation, the image and object would be identical.

Example

Question: Draw all the lines of symmetry on the following shape.

Solution:

Consider possible lines that would cut the shape into halves. To be a line of symmetry, imagine folding the shape along each line. If the fold leads to the two halves sitting exactly on top of each other, then the line is a line of symmetry.

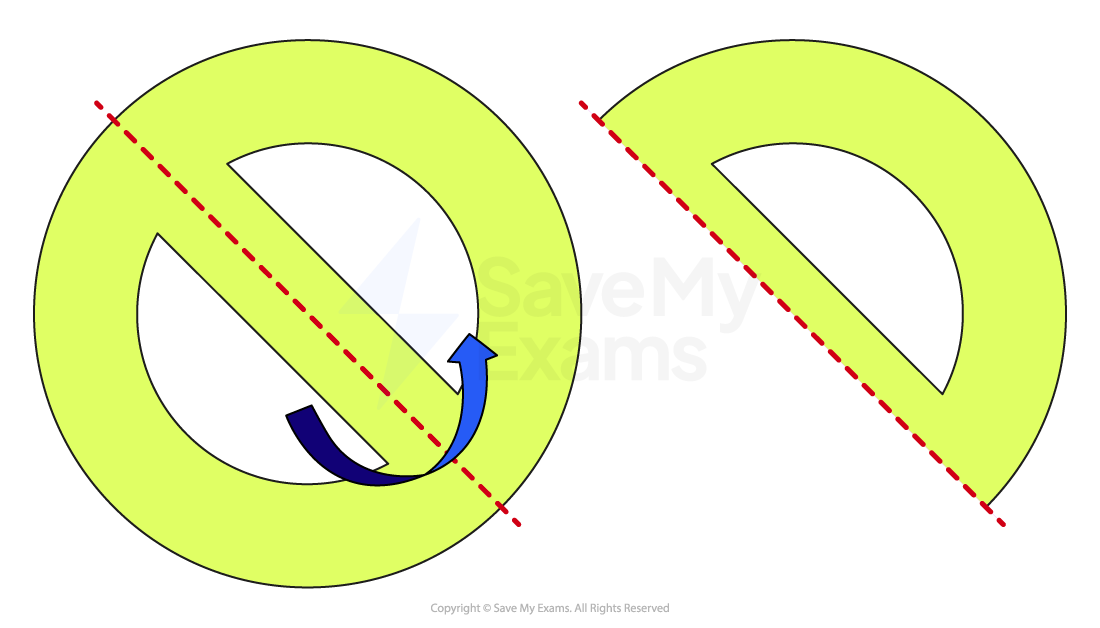
There is another line of symmetry, but that is dealt with below, as an alternative method

Alternatively, consider the reflection of the shape in possible lines of symmetry. You’d need to consider the reflection on both sides of the line (a two-way reflection) and if the whole shape looks identical then you have found a line of symmetry.

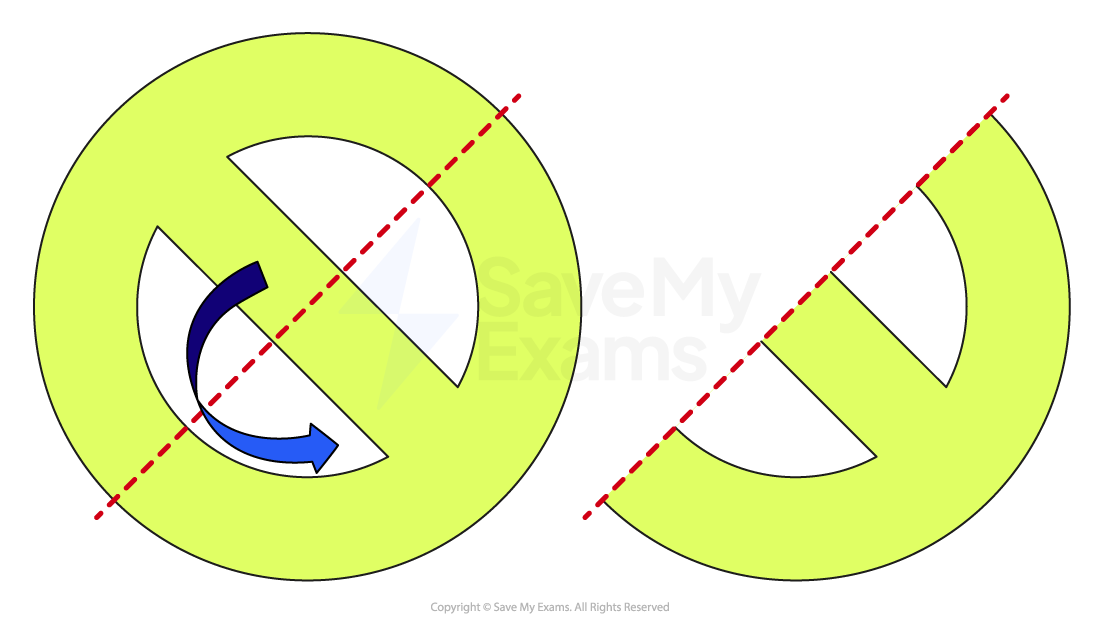
Answer:

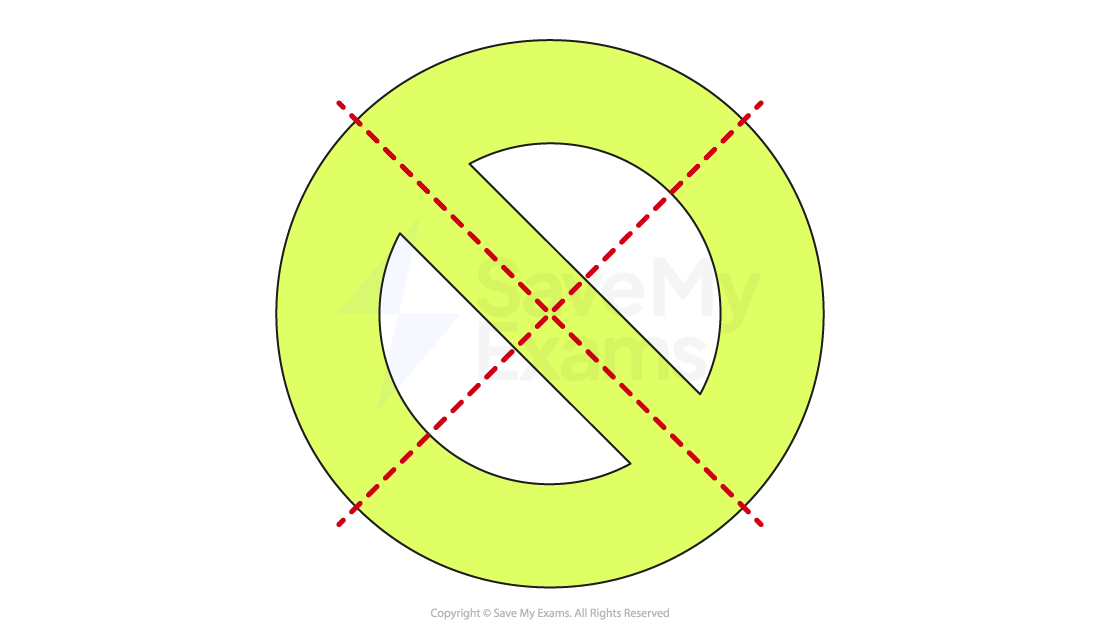
Common mistakes (and how to avoid them)

Mistake 1: Thinking that rectangles have diagonals line of symmetry

You can prove this for yourself using a sheet of paper. Fold it along a diagonal.

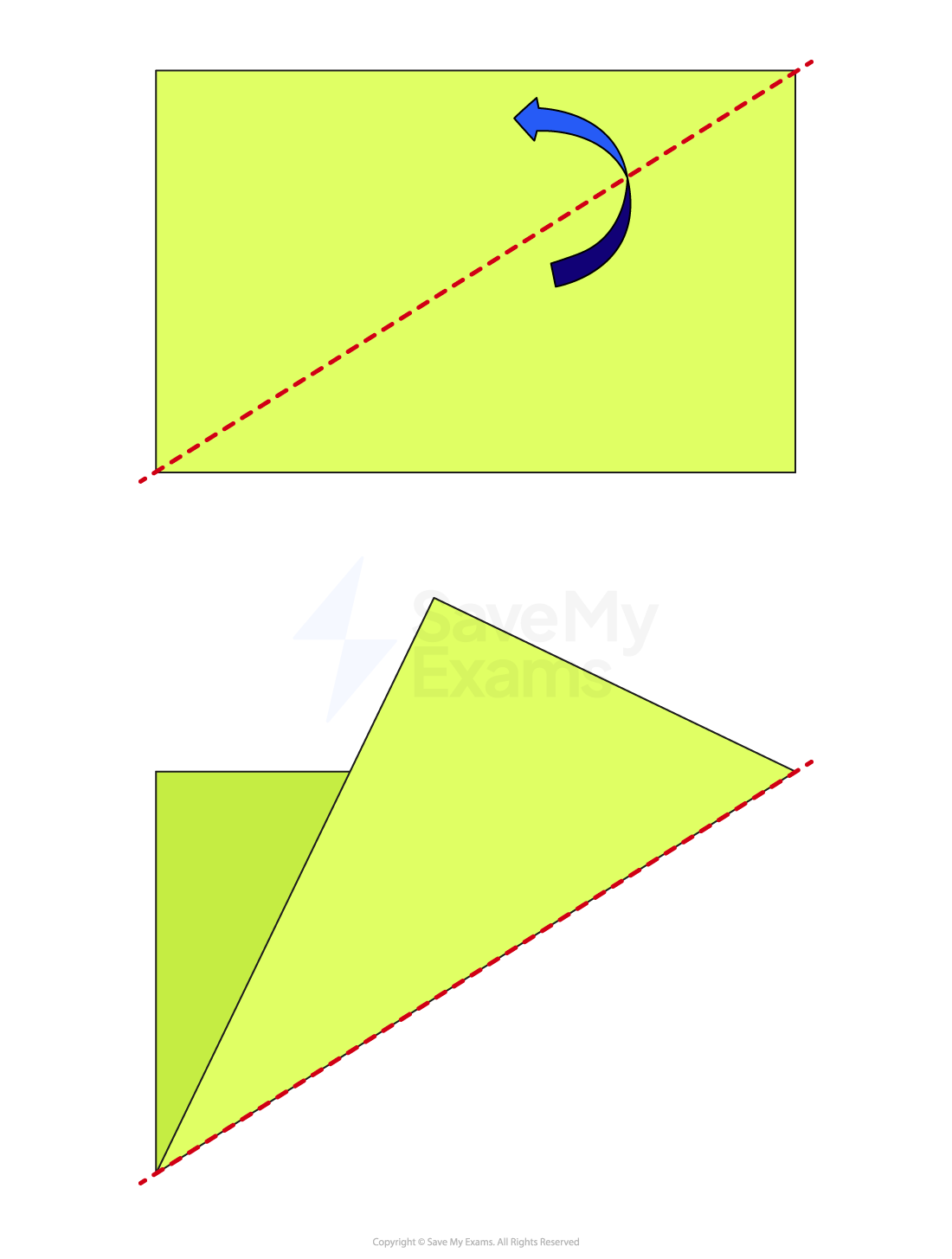
Whilst folding along the line would split the shape into two halves, they do not fit on top of each other.

Note that if we were to refer to this as a reflection (rather than a fold), the diagram above shows only half of the shape folded, the ‘upper left’ part would also be reflected (towards the ‘bottom right’).

How to avoid this: Imagine folding along any possible line of symmetry in a shape. The two halves created must overlap each other exactly. 

Mistake 2: Inaccuracies when drawing lines of symmetry

When asked to draw a line of symmetry on a given diagram, you should ensure they are drawn carefully, so their position is clear - for example, if a line of symmetry should pass through the vertex of a shape, ensure it does; ‘nearby’ might not be accepted in an exam.

How to avoid this: Use a ruler to draw the line of symmetry, taking a little extra time to line it up accurately, and make sure the ruler does not slip as you draw the line.

Frequently asked questions

What's the difference between a line of symmetry and a mirror line?

A mirror line is a line that a shape will be reflected in, and can be located inside or outside the object. Where the mirror line passes through the shape, a two-way reflection occurs.
A line of symmetry will always be inside (or on) a shape and is such that folding along it will split the shape into two halves that fit exactly on top of each other..
Questions will usually ask you to identify lines of symmetry for a given shape..

How do I know I’ve got all the lines of symmetry drawn on a shape?

For regular polygons (polygons with equal side lengths and angles, such as a square) the number of lines of symmetry will equal the number of sides (so 4 lines of symmetry for a square).

For other shapes (including irregular polygons), using a new copy of the shape to consider each possible line separately can help you see more clearly whether it is a line of symmetry. In the exam, a quick sketch of the original shape should enable you to do this.

Does a circle have any lines of symmetry?

Yes. Lots! There is no limit to the number of lines of symmetry a circle has. Any diameter (any line passing through the centre of the circle) will be a line of symmetry.

Related GCSE Mathematics glossary terms

• Symmetrical

• Reflection

• Object

• Image