Hardest IGCSE Maths Questions & How to Answer Them

Staring at a complex IGCSE Maths question that seems impossible? You're not alone.

Those final questions on the Extended paper can feel like they're stretching your brain to its limits. They can combine multiple topics and test whether you can really think like a mathematician. It can be frustrating when you know your maths but can't crack these top-end problems.

Here's the good news: once you understand what makes them difficult, learn the right approach and practise many of them, they become much more manageable.

Key takeaways

• Multi-step thinking – The hardest questions require you to combine several methods and spot connections between topics

• Unfamiliar contexts – You'll need to apply familiar maths in situations you haven't practised before

• Common traps exist – Learn the mistakes that cost students the most marks

• Problem-solving beats memorising – Success comes from understanding why methods work, not just remembering them

• Practising the hardest questions makes the hard and medium questions seem easy!

What makes an IGCSE Maths question difficult?

Not all IGCSE questions are created equal. The hardest ones share some specific characteristics. As a teacher, and as a content creator at Save My Exams (opens in a new tab), I have written a lot of worked solutions to IGCSE questions. This is what separates the hard questions from the rest:

Multi-step processes are the biggest challenge. Instead of "use Pythagoras' theorem," you might need to find a missing angle first, then use trigonometry, then apply Pythagoras. Each step builds on the last.

Unfamiliar contexts throw many students off. You know how to calculate probability. But can you apply it to a game scenario you've never seen before? Hard questions test whether you truly understand concepts, not just whether you've memorised examples.

Combined topics appear regularly in top-mark questions. You might need algebra to solve a geometry problem. Or use functions alongside transformations. These connections between topics separate strong students from exceptional ones.

Abstract reasoning challenges your logical thinking. Proof questions and algebraic manipulation require you to work with expressions and logic, not just numbers. Many students find this uncomfortable because there's no "obvious" answer to aim for.

Minimal scaffolding means you get less help. Easy questions break down into parts (a), (b), (c). Hard questions give you a single instruction and expect you to figure out all the steps yourself.

How to approach hard IGCSE Maths questions

The highest achieving students I’ve taught follow clear processes when tackling difficult questions.These include:

Read carefully – twice. Sounds obvious, but rushing causes more mistakes than anything else. Read the question once to understand what's being asked. Read it again to spot the details you missed.

Identify what you know and what you need. Write down the given information. Circle or underline key numbers. What's the question actually asking for? Sometimes the end goal isn't obvious at first glance.

Spot the hidden hints. Question wording contains clues. "Hence" means use your previous answer. "Show that" means you know the answer already – work backwards. "Give your answer in the form..." tells you how to present your final answer and could hint at which method to use.

Choose your method strategically. Multiple approaches often work. Pick the one you're most confident with. There's no prize for using the "clever" method if you make errors.

Work step-by-step, showing everything. Even if you can do steps in your head, write them down. Method marks save your grade when you make small mistakes. Plus, writing it all down helps you spot errors.

Check as you go. Does your answer make sense? If you calculated someone's height as 450 cm, something went wrong. Quick sense-checks can catch silly mistakes.

Review your working. Look back at what you wrote. Did you answer the actual question? Are your units correct? Is your final answer clearly indicated? If it's a “show that” question, is your working clear enough with enough steps shown?

Hardest IGCSE Maths questions: real examples

Let's look at questions that have really challenged students in the past. These are all real IGCSE exam questions. For each, we'll explore why it's difficult and you can view how to solve it on our site. Each question has a student-friendly model answer available, and you can use Smart Mark to assess your answers and see how many marks you would get.

Quadratic Equations & Surds - CIE 0580/42 June 2020 Q9b

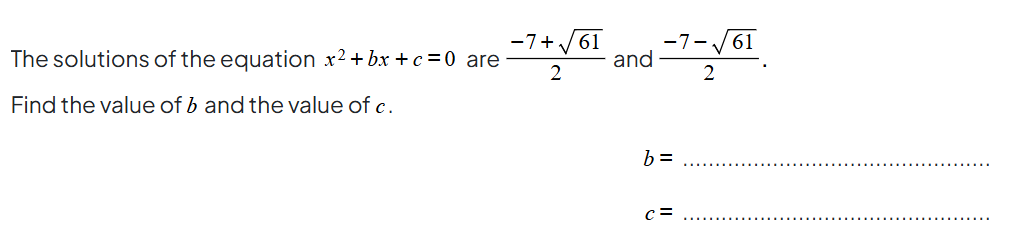
This is quite a unique question because it starts with an answer to a quadratic equation, in surd form, and asks you to find the unknown quadratic equation that goes with it. 

This is a novel concept to most students, and requires real problem solving skills and knowledge to be combined. You need knowledge of quadratic equations, as well as needing to be comfortable with manipulating surds. 

Have a go at this question, check your answers with Smart Mark, and view our solution in our Quadratic Equations exam question pack.

Circle Theorems & Trigonometry - CIE 0580/41 November 2020 Q4c

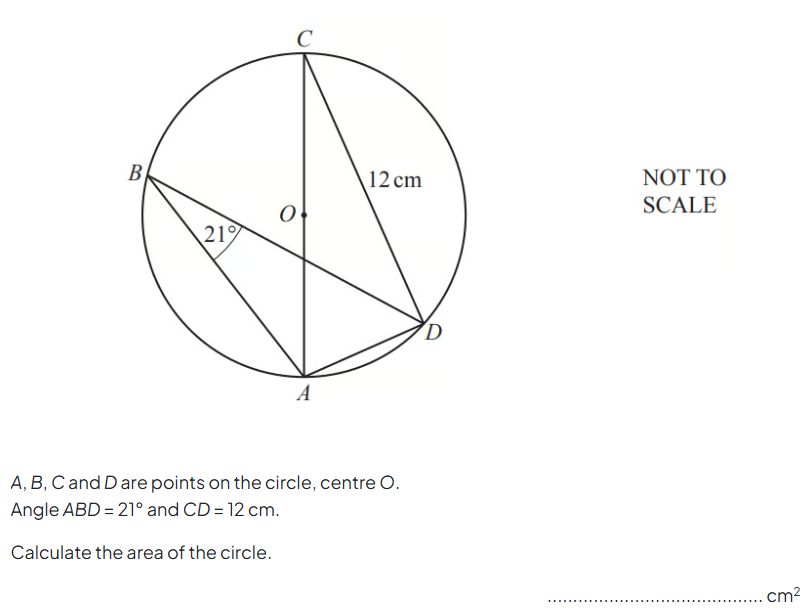
This question certainly appears to be a circle theorem question at first glance (you should be able to spot some other angles which are 21 degrees straight away!). But once you start working on it, you will find you need to use some trigonometry. You will also need to use the area of a circle formula. 

I know that the later working in this question would trip up many students, even if they have practised the “usual” style of questions on this topic. In my experience, even knowledgeable students' confidence can be knocked when it starts to look like they will need to use skills from other areas of the course. I can’t believe it was so early in the paper! 

Have a go at this question, check your answers with Smart Mark, and view our solution in our Circle Theorems exam question pack.

Surds, Volume & Algebra - Edexcel 4MA1/2H June 2023 Q23

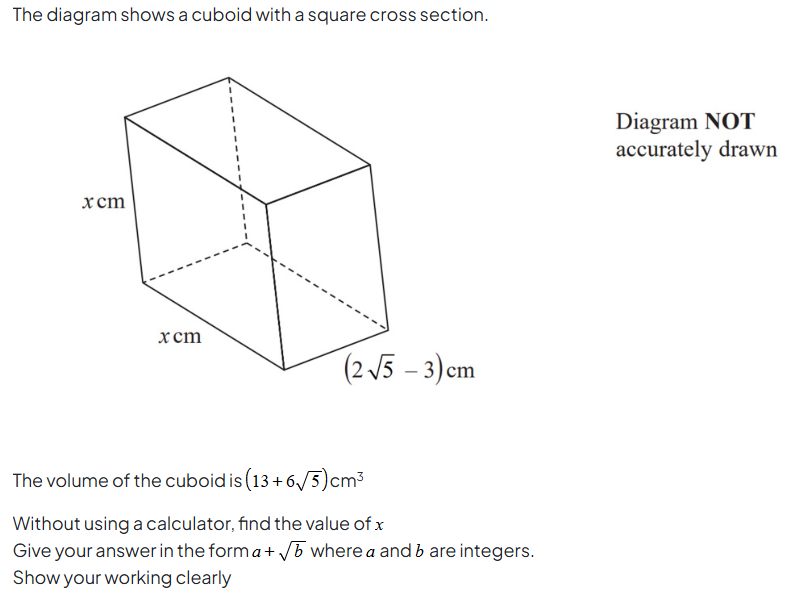
All students should be able to start on this question; writing an equation for the volume of a cuboid. Once you’ve done that though, you’ll start to notice there is still a lot to be done! 

This non-calculator question involves rearranging, rationalising the denominator of surds, and some real confidence with algebra to succeed. 

Try it yourself and see how many marks you get with Smart Mark, and then check our student friendly model answer to see how we did it. It’s in our Surds exam question pack.

Angles, Trigonometry & Areas - Edexcel 4MA1/1HR November 2020 Q22

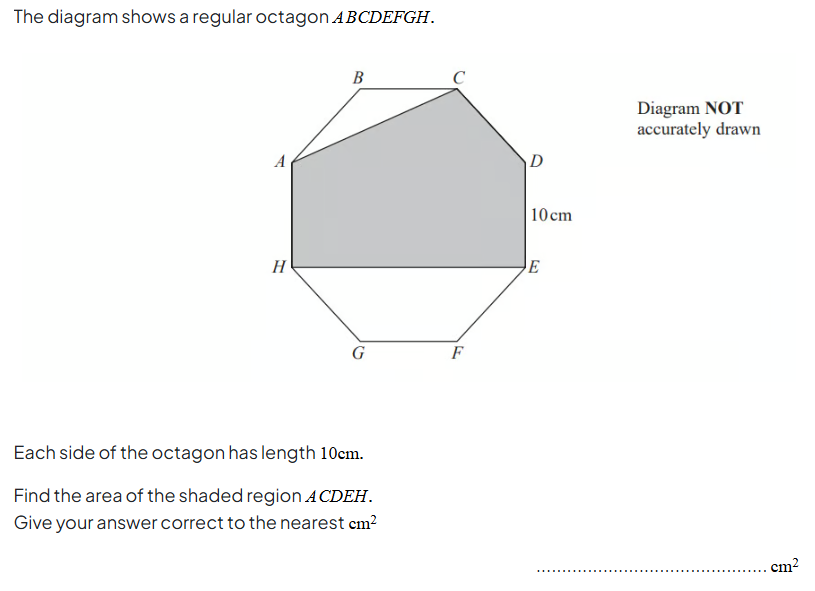
I like this style of question because I know that students struggle with questions where there isn’t an immediately obvious path to a solution. 

This is definitely one of those questions where you should start by simply seeing what you can work out. What angles do you know? What other shapes can you make by drawing some lines? 

There are certainly a lot of triangles you can form here to help you then, and then you can use your trigonometry skills. You will also need to recall some facts to do with angles in polygons (in this case an octagon) to help you. 

Why not have a go and see how far you can get? Type your working into Smart Mark and see how many marks you’d receive. Afterwards compare your answer with our own model answer from our experts. This question is from our Sine, Cosine Rule & Area of Triangles exam question pack.

Conditional Probability - CIE 0580/43 June 2018 Q4

Whether in class or in exams, I know that students often struggle with the wording of probability questions. They can be very subtle with the language they use which can completely change the maths needed to solve the question. 

With both part (a) and part (b) in this question you need to make sure you read the question carefully. The key term to look out for is almost always “replacement”. If the item is not replaced, then it is a conditional probability question. 

Luckily you do have a calculator for this one, which makes the fractions work easier, but the concepts and the set up of the question can still be tricky. I especially like part (iii) because it asks students to show their working and justify their final answer. This means your work must be clear enough for the examiner to understand. 

Try it yourself, assess your answer with Smart Mark, and view our model solution in our Conditional Probability exam question pack. 

Tips for practising difficult IGCSE Maths questions

Knowing how to approach hard questions is one thing. Actually getting better at them requires smart practice. The students I have taught who received top grades used a wide range of techniques, and a selection of my favourites are below. 

Consider timing yourself. Sometimes work slowly, focusing on understanding. Other times, set a timer to build exam speed.

Target end-of-paper questions. The last few questions on Extended papers contain the hardest content. Practice these specifically.

Use mark schemes actively. Don't just check if you got the right answer. Read how marks are allocated. Understanding what earns marks helps you structure your working. Mark schemes will also include alternate methods to consider.

Analyse your mistakes. Keep an error log. What type of mistake was it? Calculation error? Wrong method? Misread the question? Patterns will emerge.

Practice multi-step problems regularly. Your brain needs training to handle complex processes. Little and often beats cramming.

Teach someone else. Explaining a hard question to a friend cements your understanding. If you can teach it, you've mastered it.

Review examiner reports. These documents explain what went wrong for real students. Learn from their mistakes.

Frequently Asked Questions

What are the hardest topics in IGCSE Maths?

I find that the topics IGCSE Maths students consistently struggle most with are:

• Algebraic proof – requires abstract thinking many find uncomfortable

• Non-right-angled trigonometry – choosing and applying sine/cosine rule correctly

• Circle theorems – memorising theorems and recognising which one applies

• Functions – particularly inverse and composite functions

• Probability – especially conditional probability and tree diagrams

These topics appear frequently in high-mark questions. Master them and you'll be well-prepared.

Are these questions only on the extended paper?

Yes, the hardest questions appear almost exclusively on extended tier papers.

Core tier covers foundational content. The extended tier includes everything from core plus additional topics.

The final questions in the extended papers are where examiners really test top students. These questions often have the lowest success rates across all candidates.

If you're aiming for grades 7-9, you need to practice the later extended tier questions thoroughly.

Can I still get a good grade if I struggle with these questions?

Absolutely. Don't panic if the hardest questions feel impossible right now.

Grade boundaries show you don't need full marks to achieve grade 9. Missing marks on one or two very difficult questions won't ruin your grade.

However, pushing yourself with challenging questions improves your overall problem-solving skills. Even if you don't master the hardest content, attempting it strengthens your understanding of everything else.

Focus on securing marks on medium-difficulty questions first. Then gradually work up to the toughest ones.

How do I get better at problem-solving questions?

Problem-solving is a skill you build over time, through a thorough understanding of the concepts and meaningful practice. 

Break problems into smaller parts. Don't try to see the whole solution at once. Ask "what can I find first?"

Learn multiple methods. The more approaches you know, the more likely you'll spot a way forward.

Review solutions you didn't get. Understanding why a method works teaches you more than getting it right the first time.

Study worked examples actively. Don't just read solutions. Cover them up and try to reproduce the steps. Test whether you've really understood.

Build confidence gradually. Start with questions slightly above your comfort level. Gradually increase the difficulty as you improve.

Final thoughts

The hardest IGCSE Maths questions test more than memory. They test whether you can think mathematically, combine ideas, and solve problems you haven't seen before.

This is actually good news. It means that practice and understanding the content inside-out genuinely improves your performance and score. It gives you an opportunity to stand out from other candidates, so that you can achieve the highest grades.

Every difficult question you work through builds your problem-solving skills. Every mistake you analyse teaches you something new. Every method you master opens up more questions.

This should motivate you to approach these challenges with a positive mindset. Getting a hard question wrong isn't failure – it's information about what to practice next to improve.

During my teaching I found that the students who excel at IGCSE Maths aren't necessarily the "naturally gifted" ones. They're the ones who practice purposefully, learn from mistakes, and keep pushing themselves with challenging content.

You can do the same. Start with one difficult question. Work through it carefully. Learn from it. Then tackle the next one.

That's how you master the hardest IGCSE Maths questions.

Improve your grades with Save My Exams

Save My Exams is here to help you achieve the best grade possible in IGCSE Maths by offering expert-written resources specifically made for your exam board. We’ve got everything you need:

• Detailed, exam-aligned revision notes

• Exam-style questions by topic, with student friendly worked solutions

• Smart Mark to mark your answers

• Past papers with mark schemes

• Target tests to assess yourself

• Mock exams to practise the real thing

Whether you want to improve your understanding of key topics, test your knowledge, or sharpen your exam techniques, Save My Exams makes it easier and more effective for you to revise.

Explore Our IGCSE Maths Resources