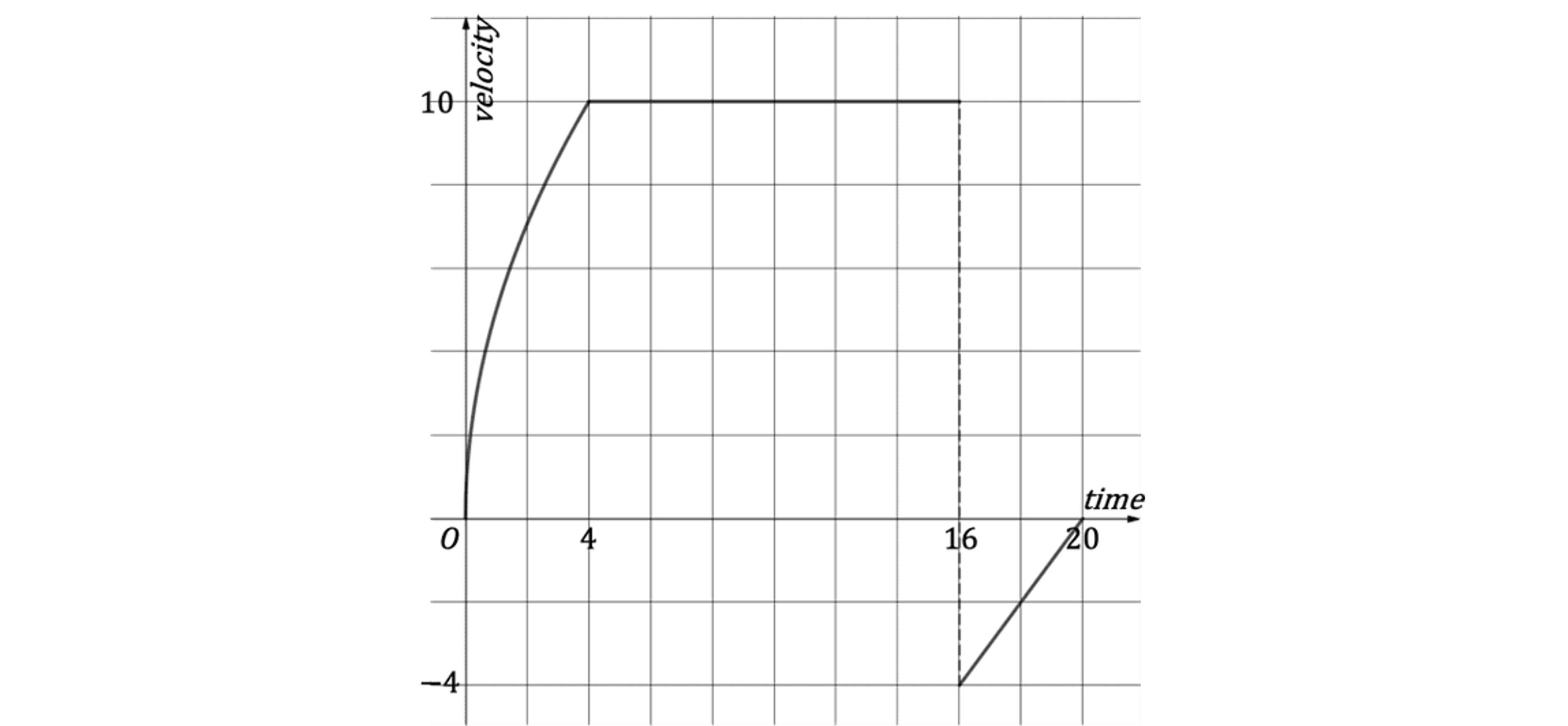
A particle moving in a straight line has displacement, m, from its initial position at time,
seconds, given by the equation
Find the displacement of the particle after 12 seconds.
(i) Find an expression for the velocity after seconds.
(ii) Find the velocity of the particle after 8 seconds.
Did this page help you?