Study GuidesExam QuestionsPast PapersMock Exams
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedExam QuestionsUnit 6: Energy & Momentum of Rotating SystemsRotational Kinetic Energy, Torque & Work

Rotational Kinetic Energy, Torque & Work (College Board AP® Physics 1: Algebra-Based): Exam Questions

32 mins18 questions

Select a download format for Rotational Kinetic Energy, Torque & Work

Scroll for more

Select an answer set to view for
Rotational Kinetic Energy, Torque & Work

1a
Sme Calculator2 marks
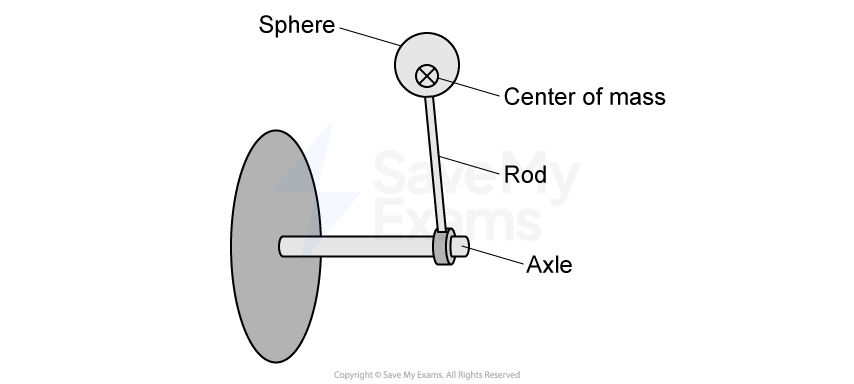
A sphere attached to a rod on an axle via a rod. The center of mass of the system is located just below the center of the sphere.

Figure 1

A rod with a sphere attached to the end is connected to a horizontal mounted axle and carefully balanced so that it rests in a position vertically upward from the axle. The center of mass of the rod sphere system is indicated with a circled times, as shown in Figure 1. The sphere is lightly tapped, and the rod-sphere system rotates clockwise with negligible friction about the axle due to the gravitational force.

A student takes a video of the rod rotating from the vertically upward position to the vertically downward position. Figure 2 shows five frames (still shots) that the student selected from the video.

Note: these frames are not equally spaced apart in time.

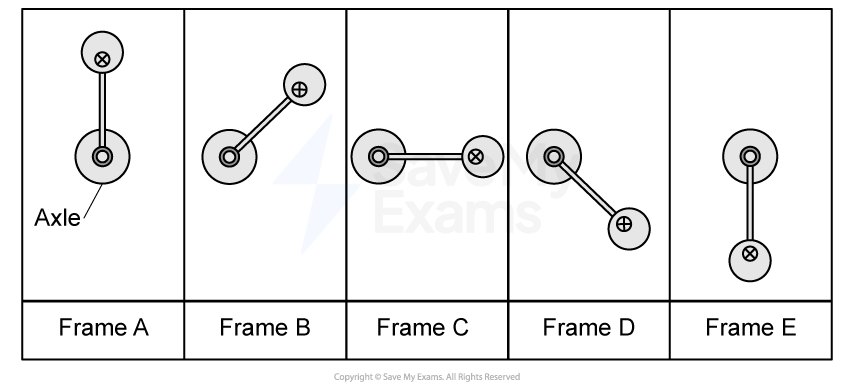
Five still frames, A to E, from a video of the rotating rod-sphere system. Frame A: the sphere is positioned vertically upward. Frame B: the sphere is between the vertically upward and horizontal positions. Frame C: the sphere is positioned horizontally. Frame D: the sphere is between the vertically downward and horizontal positions. Frame E: the sphere is positioned vertically downward.

Figure 2

In which of the frames of the video in Figure 2 is the rotational kinetic energy of the rod-sphere system the greatest? Justify your answer using qualitative reasoning beyond referencing equations.

How did you do?

1b
Sme Calculator3 marks
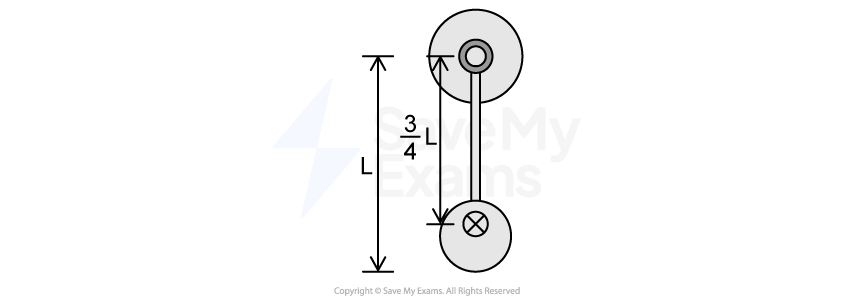
A rod-sphere system hanging vertically downward with respect to the axle. Two lengths are indicated, length "L" represents the distance from axle to the bottom of the sphere, and length "3/4 L" represents the distance from the axle to the center of mass.

Figure 3

The rod-sphere system has mass M and length L, and the center of mass is located a distance 3 over 4 L from the axle, as shown in Figure 3.

Derive an expression for the change in kinetic energy of the rod-sphere-Earth system from the moment shown in Frame A to the moment shown in Frame E. Express your answer in terms of M, L, and fundamental constants, as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

How did you do?

1c
Sme Calculator3 marks

A student makes the following claim:

"The rod and sphere gain kinetic energy, even if the Earth is not included in the system".

Justify whether or not the student's claim is correct by referring to the equation you derived in part b).

How did you do?

Did this page help you?

2a
Sme Calculator4 marks
A wheel mounted on an axle at its center with a block hanging from a string wound around the wheel. The block hangs from a height above the floor below.

Figure 1

A group of students have a wheel mounted on a horizontal axle and a small block of mass 0.2 space kg attached to one end of a light string. The other end of the string is attached to the wheel's rim and wrapped around it several times, as shown in Figure 1. When the block is released from rest and begins to fall, the wheel begins to rotate with negligible friction.

The students are asked to determine the rotational inertia I of the wheel. The students measure the angular velocity omega of the wheel as the block falls a distance d and determine the translational kinetic energy K subscript T of the block immediately before it reaches the floor.

The student's measurements for different falling distances are shown in the following table.

Falling distance,

d space open parentheses straight m close parentheses

Angular velocity of the wheel,

omega space open parentheses rad divided by straight s close parentheses

Translational kinetic energy,

K subscript T space open parentheses straight J close parentheses

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

0.10

2.4

0.08

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

0.30

3.8

0.16

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

0.50

5.1

0.36

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

0.70

6.0

0.47

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

0.90

6.7

0.59

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

1.10

7.5

0.72

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎

i) Indicate two quantities that could be plotted to yield a linear graph whose slope could be used to calculate an experimental value for the rotational inertia I of the wheel. Use the blank columns in the table to list any calculated quantities you will graph other than the data provided.

Vertical Axis: ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ Horizontal Axis: ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽

ii) Plot the data points for the quantities indicated in part c)i) on the graph provided. Clearly scale and label all axes, including units, as appropriate.

Rectangular grid with small squares, divided into larger sections by thicker lines, resembling graph paper for mathematical or design purposes.

iii) Draw a best-fit line to the data graphed in part c)ii).

How did you do?

2b
Sme Calculator2 marks

Calculate an experimental value for the rotational inertia of the wheel using the best-fit line that you drew in part c)iii.

How did you do?

Did this page help you?

3
Sme Calculator3 marks
A ball on the ground just below a pivot connected to a horizontal rod, with a curved dashed line representing the rotational path of the end of the rod once released.

Figure 1

A system consists of a small sphere of mass m and radius R at rest on a horizontal surface and a uniform rod of mass M space equals space 2 m and length l attached at one end to a pivot with negligible friction, where R space much less-than space l. There is negligible friction between the surface and the sphere. The rod is held horizontally as shown in Figure 1, and then is released from rest. The total rotational inertia of the rod about the pivot is 1 third M l squared. After the rod is released, the rod swings down and strikes the sphere head-on.

Starting with conservation of energy, derive an expression for the angular speed of the rod just before striking the sphere in terms of the length l and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

How did you do?

Did this page help you?