Differentiating Inverse Trigonometric Functions (DP IB Analysis & Approaches (AA)): Revision Note

Author

Paul

Last updated

5 June 2025

Differentiating Inverse Trigonometric Functions

What are the inverse trigonometric functions?

arcsin, arccos and arctan are functions defined as the inverse functions of sine, cosine and tangent respectively
- $\arcsin (\frac{\sqrt{3}}{2}) = \frac{π}{3}$ which is equivalent to $\sin (\frac{π}{3}) = \frac{\sqrt{3}}{2}$
- $\arctan (- 1) = \frac{3 π}{4}$ which is equivalent to $\tan (\frac{3 π}{4}) = - 1$

What are the derivatives of the inverse trigonometric functions?

$f (x) = \arcsin x$
- $f' (x) = \frac{1}{\sqrt{1 - x^{2}}}$
$f (x) = \arccos x$
- $f' (x) = - \frac{1}{\sqrt{1 - x^{2}}}$
$f (x) = \arctan x$
- $f' (x) = \frac{1}{1 + x^{2}}$
Unlike other derivatives these look completely unrelated at first
- their derivation involves use of the identity $\cos^{2} x + \sin^{2} x \equiv 1$
- hence the squares and square roots!
All three are given in the formula booklet
Note with the derivative of $\arctan x$ that $(1 + x^{2})$ is the same as $(x^{2} + 1)$

How do I show or prove the derivatives of the inverse trigonometric functions?

For $y = \arcsin x$
- Rewrite, $\sin y = x$
- Differentiate implicitly, $\cos y \frac{d y}{d x} = 1$
- Rearrange, $\frac{d y}{d x} = \frac{1}{\cos y}$
- Using the identity $\cos^{2} y \equiv 1 - \sin^{2} y$ rewrite, $\frac{d y}{d x} = \frac{1}{\sqrt{1 - \sin^{2} y}}$
- Since, $\sin y = x$ , $\frac{d y}{d x} = \frac{1}{\sqrt{1 - x^{2}}}$
Similarly, for $y = \arccos x$
- $\cos y = x$
- $- \sin y \frac{d y}{d x} = 1$
- $\frac{d y}{d x} = - \frac{1}{\sin y}$
- $\frac{d y}{d x} = - \frac{1}{\sqrt{1 - \cos^{2} y}}$
- $\frac{d y}{d x} = - \frac{1}{\sqrt{1 - x^{2}}}$
Notice how the derivative of $y = \arcsin x$ is positive but is negative for $y = \arccos x$
- This subtle but crucial difference can be seen in their graphs
  - $y = \arcsin x$ has a positive gradient for all values of $x$ in its domain
  - $y = \arccos x$ has a negative gradient for all values of $x$ in its domain

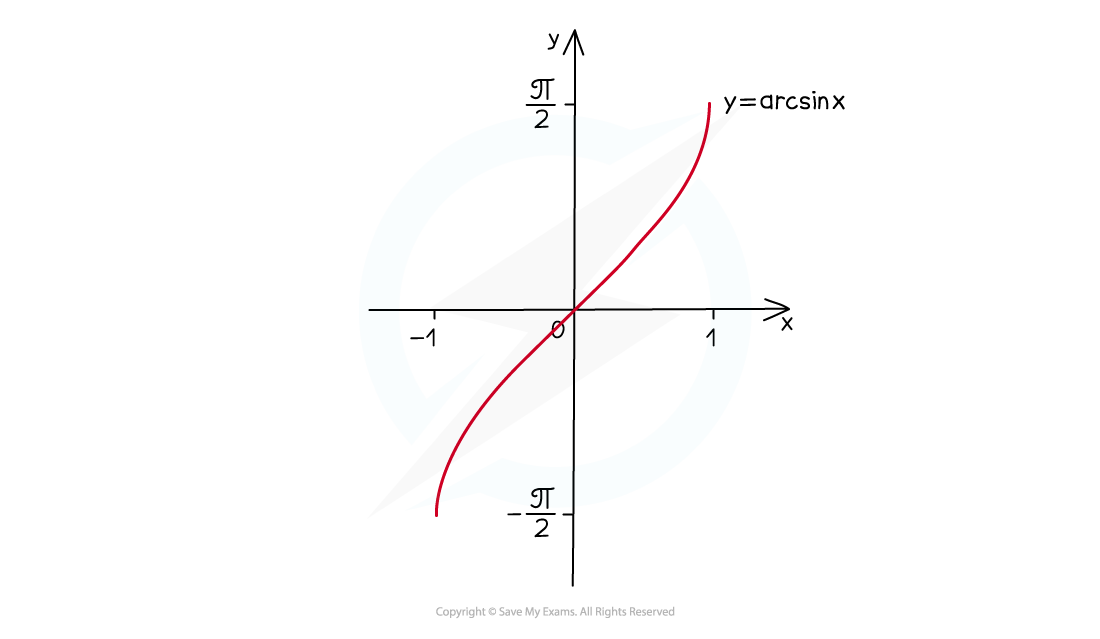
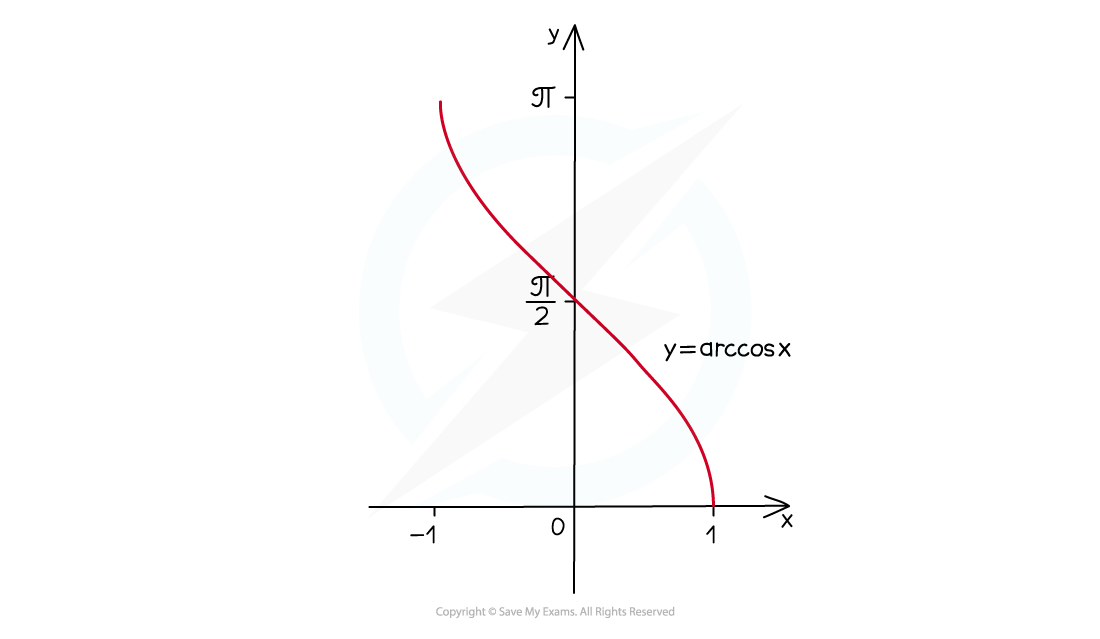
What do the derivative of inverse trig look like with a linear function of x?

For linear functions of the form $a x + b$
$f (x) = \arcsin (a x + b)$
- $f' (x) = \frac{a}{\sqrt{1 - {(a x + b)}^{2}}}$
$f (x) = \arccos (a x + b)$
- $f' (x) = \frac{a}{\sqrt{1 - {(a x + b)}^{2}}}$
$f (x) = \arctan (a x + b)$
- $f' (x) = \frac{a}{1 + {(a x + b)}^{2}}$
These are not in the formula booklet
- they can be derived from chain rule
- they are not essential to remember
- they are not commonly used

Examiner Tips and Tricks

For $f (x) = \arctan x$ the terms on the denominator can be reversed (as they are being added rather than subtracted)
- $f' (x) = \frac{1}{1 + x^{2}} = \frac{1}{x^{2} + 1}$
- Don't be fooled by this, it sounds obvious but on awkward "show that" questions it can be off-putting!

Worked Example

a) Show that the derivative of $\arctan x$ is $\frac{1}{1 + x^{2}}$

b) Find the derivative of $\arctan (5 x^{3} - 2 x)$ .

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Differentiating Reciprocal Trigonometric FunctionsNext:Differentiating Exponential & Logarithmic Functions

Differentiating Inverse Trigonometric Functions (DP IB Analysis & Approaches (AA)): Revision Note

Differentiating Inverse Trigonometric Functions

What are the inverse trigonometric functions?

What are the derivatives of the inverse trigonometric functions?

How do I show or prove the derivatives of the inverse trigonometric functions?

What do the derivative of inverse trig look like with a linear function of x?

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Number & Algebra

Number & Algebra Toolkit

Standard Form

Laws of Indices

Partial Fractions

Exponentials & Logs

Introduction to Logarithms

Laws of Logarithms

Solving Exponential Equations

Sequences & Series

Language of Sequences & Series

Sigma Notation

Arithmetic Sequences & Series

Geometric Sequences & Series

Applications of Sequences & Series

Compound Interest & Depreciation

Simple Proof & Reasoning

Proof by Deduction

Disproof by Counter Example

Proof by Induction & Contradiction

Proof by Induction

Proof by Contradiction

Binomial Theorem

Binomial Coefficients & Pascal's Triangle

Binomial Theorem

Extension of The Binomial Theorem

Permutations & Combinations

Counting Principles

Permutations

Combinations

Complex Numbers

Introduction to Complex Numbers

Operations with Complex Numbers

Modulus & Argument

Introduction to Argand Diagrams

Further Complex Numbers

Geometry of Complex Numbers

Modulus-Argument (Polar) Form

Exponential (Euler's) Form

Conversion between Forms of Complex Numbers

Complex Roots of Polynomials

De Moivre's Theorem

Proof of De Moivre's Theorem

Roots of Complex Numbers

Systems of Linear Equations

Systems of Linear Equations

Solving Systems Using Row Reduction

Number of Solutions to a System

2. Functions

Linear Functions & Graphs

Equations of a Straight Line

Parallel & Perpendicular Lines

Quadratic Functions & Graphs

Quadratic Functions

Factorising Quadratics

Completing the Square

Solving Quadratic Equations

Quadratic Inequalities

Discriminants

Functions Toolkit

Language of Functions

Composite Functions

Inverse Functions

Odd & Even Functions

Periodic Functions

Self-Inverse Functions

Graphing Functions & Their Key Features

Intersecting Graphs

Other Functions & Graphs

Exponential & Logarithmic Functions

Solving Equations Analytically