Area Between 2 Curves (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Area between 2 curves
What do we mean by 'area between two curves'?
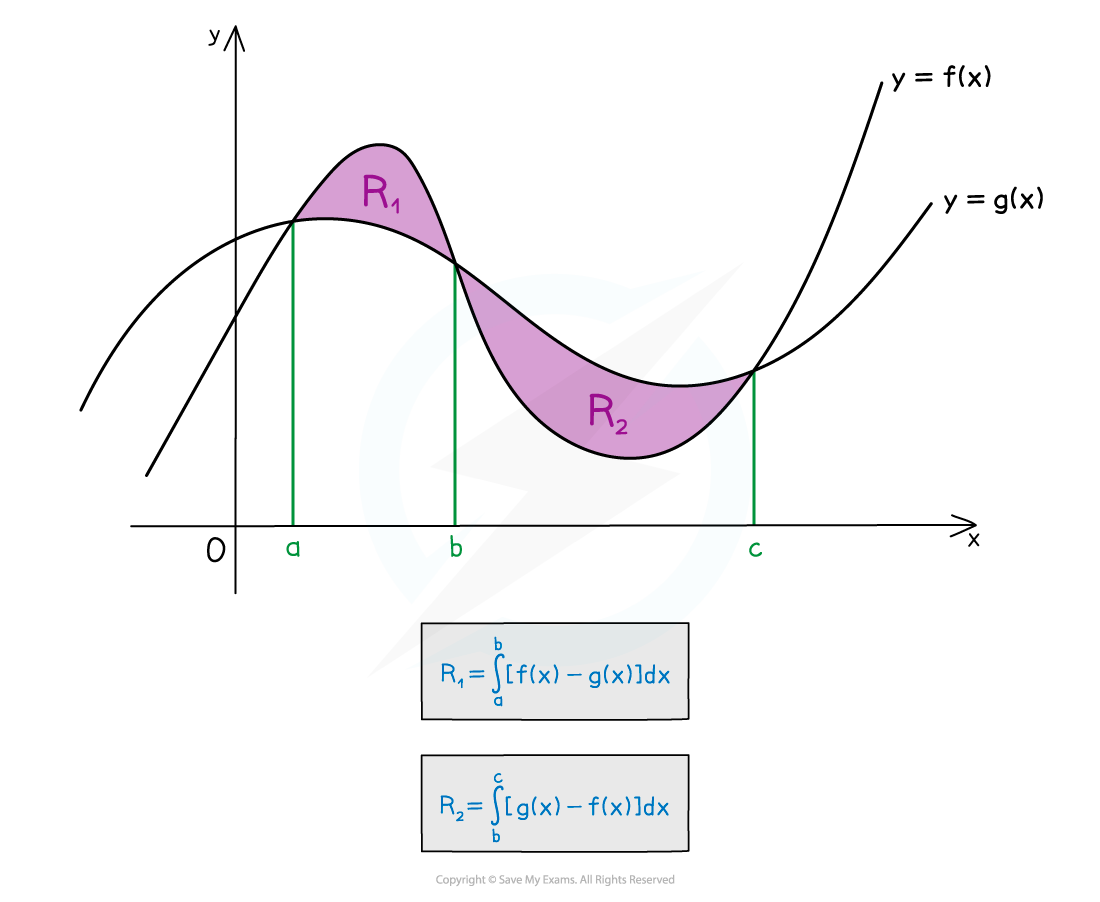
Areas whose boundaries include two curves can be found by integration
The area between two curves will be the difference of the areas under the two curves
both areas will require a definite integral
Finding points of intersection may involve a more awkward equation than solving for a curve and a line
How do I find the area between two curves?
STEP 1
If not given, sketch the graphs of both curves on the same diagram
You can use a GDC to help with this step
STEP 2
Find the intersections of the two curves
If no diagram is given this will help identify the area(s) to be found
STEP 3
For each area (there may only be one) determine which curve is the ‘upper’ boundary
For each area, write a definite integral of the form
where
is the function for the ‘upper’ boundary and
is the function for the ‘lower’ boundary
Examiner Tips and Tricks
Be careful when there is more than one region – the ‘upper’ and ‘lower’ boundaries will often switch between regions!
STEP 4
Evaluate the definite integrals and sum them up to find the total area
Examiner Tips and Tricks
As always, sketching a diagram, or adding info to a diagram that is given, is very helpful in questions like this. On a calculator paper you can use your GDC to help.
Also note that you don't have to worry about areas being below the -axis with area between two curves. As long as you have the 'upper' and 'lower' curves the right way round,
inside the integrals will always be positive. This means you can never have a 'negative integral'.
Worked Example
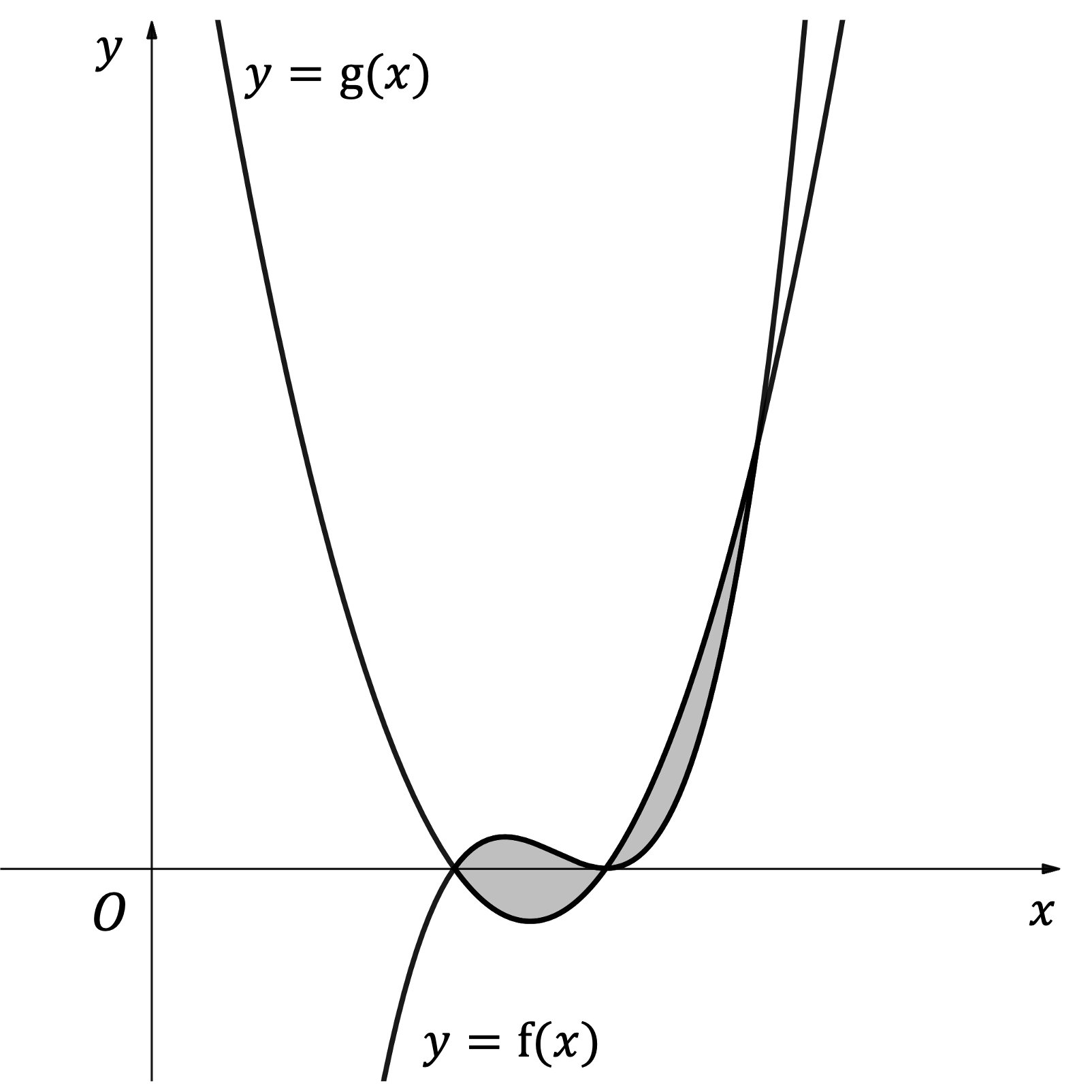
The diagram below shows the curves with equations and
where
and
.
Find the area of the shaded region.
Answer:


Unlock more, it's free!
Did this page help you?