Modulus Equations & Inequalities (DP IB Analysis & Approaches (AA)): Revision Note

Modulus equations

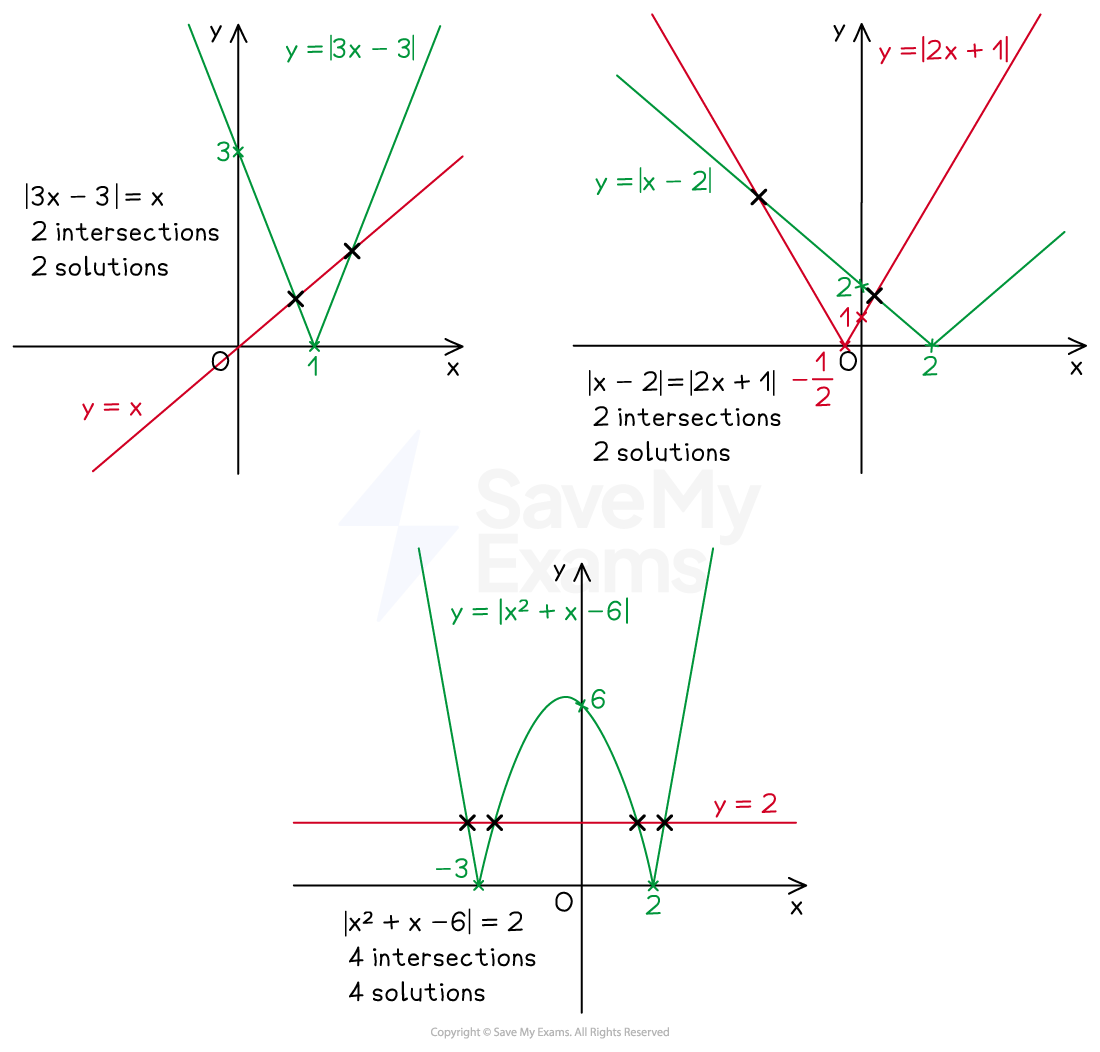
How do I solve modulus equations graphically?

• To solve (or ) graphically

  • Draw and (or ) into your GDC

    • Find the -coordinates of the points of intersection

How do I solve modulus equations using algebra?

• To solve either or using algebra, the process is the same:

  • split into two equations

    • 

    • 

  • Solve both equations

  • Check that the solutions work in the original equation

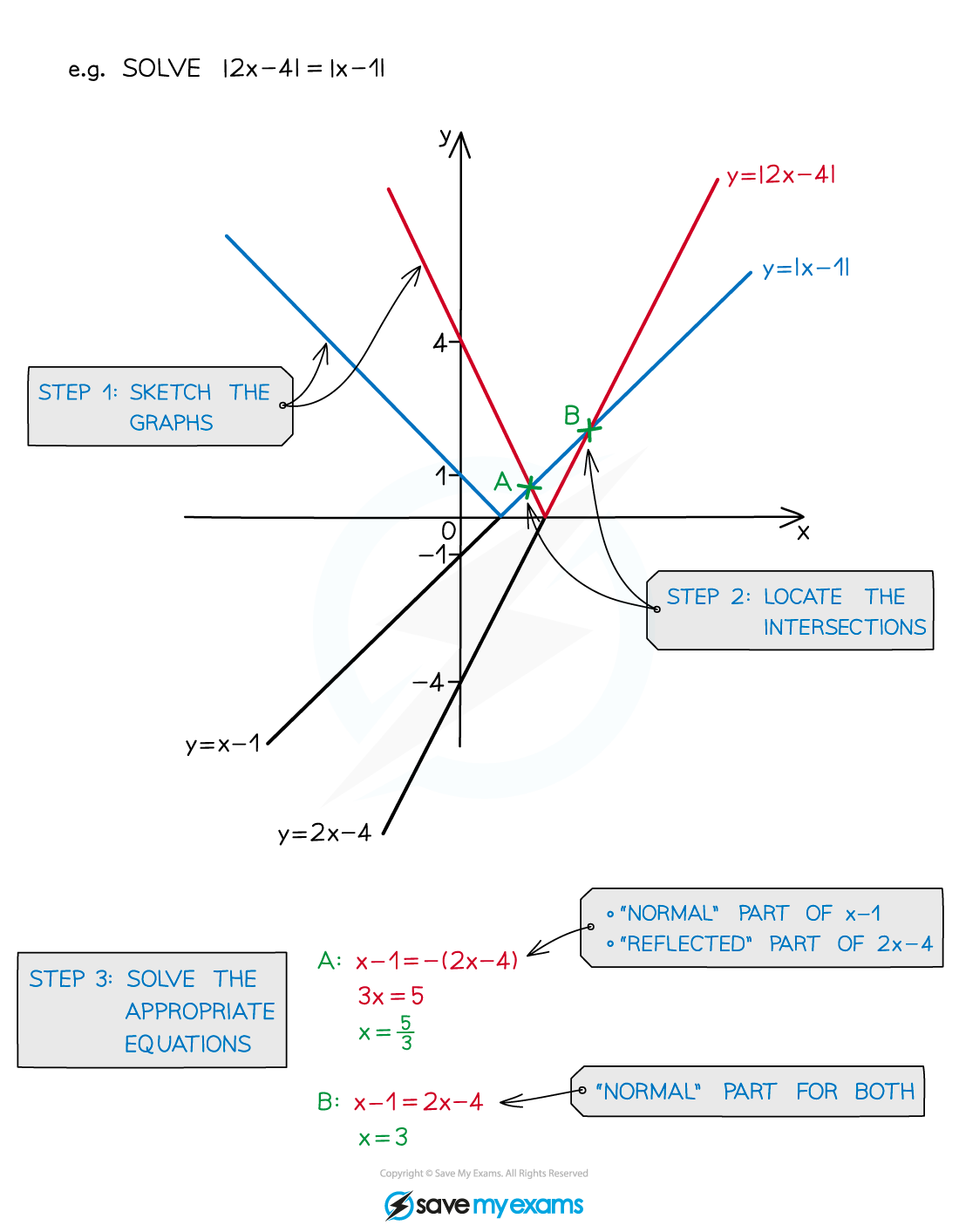
• e.g. splits into and

  • the first equation gives 

  • but is not a solution to 

    • as and 

  • the second equation gives 

    • which does satisfy so is the solution

• A sketch can help, even when solving algebraically

Modulus inequalities

How do I solve modulus inequalities?

• To solve modulus inequalities

  • first solve the modulus equation

    • by replacing the inequality sign with =

  • then use a graphical method to find the intervals of that satisfy the inequality

• To solve , , or where

  • is graph 1

  • is graph 2

  • STEP 1
    Sketch and

  • STEP 2
    Locate the -coordinates of the points of intersection

    • these would be -axis intercepts if

  • STEP 3
    Determine which part(s) of the graph(s) satisfy the inequality

    • or are where graph 1 is below than graph 2

    • or are where graph 1 is above than graph 2

  • STEP 4
    Write the range of values of for these regions

    • using strict inequalities if or

    • or 'equal to' inequalities if or

• An alternative method is to use a sign table

  • e.g. where you substitute a numerical value from each of the possible intervals of into the original inequality

    • The solutions are the regions for which the original inequality is true