International A Level (IAL)MathsEdexcelStatistics 2Revision NotesStatistical DistributionsPoisson DistributionCalculating Poisson Probabilities

Calculating Poisson Probabilities (Edexcel International A Level (IAL) Maths): Revision Note

Exam code: YMA01

Amber

Author

Amber

Last updated

Calculating Poisson Probabilities

Throughout this section we will use the random variable X tilde Po left parenthesis lambda right parenthesis  . For a Poisson distribution, the probability of a X taking a non-integer or negative value is always zero. Therefore any values mentioned in this section (other than λ) will be assumed to be non-negative integers.

Where does the formula for a Poisson distribution come from?

  • The formula for calculating an individual Poisson probability is

    • straight P left parenthesis X equals r right parenthesis equals p subscript r equals e to the power of negative lambda end exponent cross times fraction numerator lambda to the power of r over denominator r factorial end fraction for r = 0, 1, 2 ,...., n

  • The derivation of the formula comes from the binomial distribution, however it is outside the scope of this syllabus and will not be proved here

    • Whilst the binomial distribution relies on knowing a fixed number of trials, the Poisson can allow for any number of trials within a time period

    • Only the mean number of occurrences of an event within the given period needs to be known

How do I calculate the cumulative probabilities for a Poisson distribution? 

  • Most of the time the value of λ will be in the table for the 'Poisson Cumulative Distribution Function' in the formula booklet

  • begin mathsize 16px style straight P left parenthesis X less or equal than x right parenthesis end style is asking you to find the probabilities of all values up to and including x   

    • This will be the value in the row of x

  • begin mathsize 16px style P left parenthesis X less than x right parenthesis end style is asking you to find the probabilities of all values up to but not including x

    • This means all values that are less than x

    • This will be the value in the row of x - 1

      • begin mathsize 16px style straight P left parenthesis X less or equal than x minus 1 right parenthesis end style

  • begin mathsize 16px style straight P left parenthesis X greater or equal than x right parenthesis end style is asking you to find the probabilities of all values greater than and including x

    • This means all values that are at least x

    • As there is not a fixed number of trials this includes an infinite number of possibilities

    • To calculate this, use the identity begin mathsize 16px style P left parenthesis X greater or equal than x right parenthesis equals 1 minus P left parenthesis X less than x right parenthesis end style

      • Using above we get: begin mathsize 16px style straight P left parenthesis X greater or equal than x right parenthesis equals 1 minus straight P left parenthesis X less or equal than x minus 1 right parenthesis end style

  • begin mathsize 16px style P left parenthesis X greater than x right parenthesis end style is asking you to find the probabilities of all values greater than but not including x 

    • This means all values that are more than x

    • Rewrite begin mathsize 16px style P left parenthesis X greater than x right parenthesis equals 1 minus P left parenthesis X less or equal than x right parenthesis end style as to calculate this

  • If calculating begin mathsize 16px style P left parenthesis a less or equal than X less or equal than b right parenthesis end style then calculate begin mathsize 16px style straight P left parenthesis X less or equal than b right parenthesis minus straight P left parenthesis X less or equal than a minus 1 right parenthesis end style

    • This is the same idea as for the binomial distribution

How do I calculate the cumulative probabilities for a Poisson distribution if λ is not in the table?

  • In the unlikely case that λ is not in the table

    • Use the formula to find the individual probabilities and then add them up

    • Make sure you are confident working with inequalities for discrete values

    • Only integer values will be included so it is easiest to look at which integer values you should include within your calculation

    • Sometimes it is quicker to find the probabilities that are not being asked for and subtract from one

  • Having to type a lot of calculations into your calculator can be time consuming and cause errors

  • Consider the calculation begin mathsize 16px style P left parenthesis X less or equal than 3 right parenthesis equals e to the power of negative lambda end exponent cross times fraction numerator lambda to the power of 0 over denominator 0 factorial end fraction plus e to the power of negative lambda end exponent cross times fraction numerator lambda to the power of 1 over denominator 1 factorial end fraction plus e to the power of negative lambda end exponent cross times fraction numerator lambda squared over denominator 2 factorial end fraction plus e to the power of negative lambda end exponent cross times fraction numerator lambda cubed over denominator 3 factorial end fraction end style

    • Note that e to the power of negative lambda end exponent exists in every term and can be factorised out

    • Recall that begin mathsize 16px style lambda to the power of 0 equals 1 end style and 0! = 1

    • Recall also that begin mathsize 16px style lambda to the power of 1 equals lambda end style and 1! = 1

  • This calculation could be factorised and simplified to

    • begin mathsize 16px style P left parenthesis X less or equal than 3 right parenthesis equals e to the power of negative lambda end exponent open parentheses 1 plus lambda plus fraction numerator lambda squared over denominator 2 factorial end fraction plus fraction numerator lambda cubed over denominator 3 factorial end fraction close parentheses end style 

    • This is much simpler and easier to type into your calculator in exam conditions

How do I change the mean for a Poisson distribution?

  • Sometimes the mean may be given for a different interval of time or space than that which you need to calculate the probability for

  • A given value of λ can be adjusted to fit the necessary time period

    • For example if a football team score a mean of 2 goals an hour and we want to find the probability of them scoring a certain number of goals in a 90 minute game, then we would use the distribution X ~ Po(3)   

      • 90 = 1.5 × 60 so use 1.5λ

Worked Example

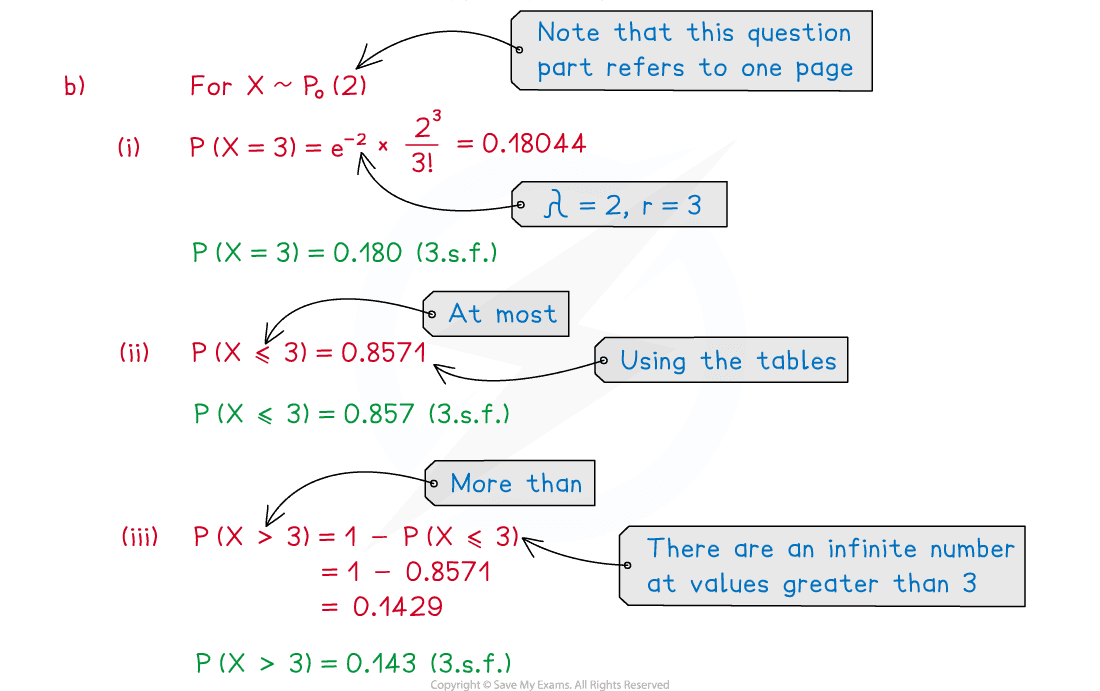
Xiao makes silly mistakes in his maths homework at a mean rate of 2 per page.

(a) Define a suitable distribution to model the number of silly mistakes Xiao would make in a piece of homework that is five pages long.

(b) Find the probability that in any random page of Xiao’s homework book there are

Answer:

(i) exactly three silly mistakes

(ii) at most three silly mistakes

(iii) more than three silly mistakes.

1-2-2-calculating-poisson-probabilities-we-solution-part-1
1-2-2-calculating-poisson-probabilities-we-solution-part-2

Examiner Tips and Tricks

  • Look carefully at the given time or space interval to check if you need to change the mean before carrying out calculations.

    • Be prepared for this to change between question parts!

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:The Poisson DistributionNext:Probability Density Function
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.