IBMathsDPAnalysis & Approaches (AA)HLRevision Notes5. CalculusTechniques & Applications of IntegrationIntegrating Trigonometric, Exponential & Reciprocal Functions

Integrating Trigonometric, Exponential & Reciprocal Functions (DP IB Analysis & Approaches (AA)): Revision Note

Paul

Author

Paul

Last updated

DP Analysis & Approaches (AA): HLDP Applications & Interpretation (AI): HLDP Analysis & Approaches (AA): SL

Did this video help you?

Integrating Trig Functions

How do I integrate sin, cos and sec^2?

  • The antiderivatives for sine and cosine are

bold space bold integral bold sin bold space bold italic x bold space bold d bold italic x bold equals bold minus bold cos bold space bold italic x bold plus bold italic c

bold space bold integral bold cos bold space bold italic x bold space bold d bold italic x bold equals bold sin bold space bold italic x bold plus bold italic c

wherebold space bold italic c is the constant of integration

  • Also, from the derivative ofspace tan space x

bold space bold integral bold sec to the power of bold 2 bold space bold italic x bold space bold d bold italic x bold equals bold tan bold space bold italic x bold plus bold italic c

  • The derivatives ofspace sin space x comma space cos space x andspace tan space x are in the formula booklet

    • so these antiderivatives can be easily deduced

  • For the linear functionbold space bold italic a bold italic x bold plus bold italic b, wherespace bold italic a andspace bold italic b are constants,

bold space bold integral bold sin bold space bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis bold space bold d bold italic x bold equals bold minus bold 1 over bold italic a bold cos bold space bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis bold plus bold italic c

bold space bold integral bold cos bold space bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis bold space bold d bold italic x bold equals bold 1 over bold italic a bold sin bold space bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis bold plus bold italic c

bold space bold integral bold sec to the power of bold 2 bold space bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis bold space bold d bold italic x bold equals bold 1 over bold a bold tan bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis bold plus bold italic c

  • For calculus with trigonometric functions angles must be measured in radians

    • Ensure you know how to change the angle mode on your GDC

Examiner Tips and Tricks

  • The formula booklet can be used to find antiderivatives from the derivatives

    • Make sure you have the page with the section of standard derivatives open 

    • Use these backwards to find any antiderivatives you need

    • Remember to add 'c', the constant of integration, for any indefinite integrals 

Worked Example

a) Find, in the formspace straight F left parenthesis x right parenthesis plus c, an expression for each integral

  1. space integral cos space x space straight d x

  2. space integral sec squared space stretchy left parenthesis 3 x minus straight pi over 3 stretchy right parenthesis space straight d x

5-4-1-ib-hl-ai-aa-extraaa-we1a-soltn

b)       A curve has equationspace y equals integral 2 sin open parentheses 2 x plus straight pi over 6 close parentheses space straight d x.

 The curve passes through the point with coordinatesspace open parentheses straight pi over 3 comma space square root of 3 close parentheses.

Find an expression forspace y.

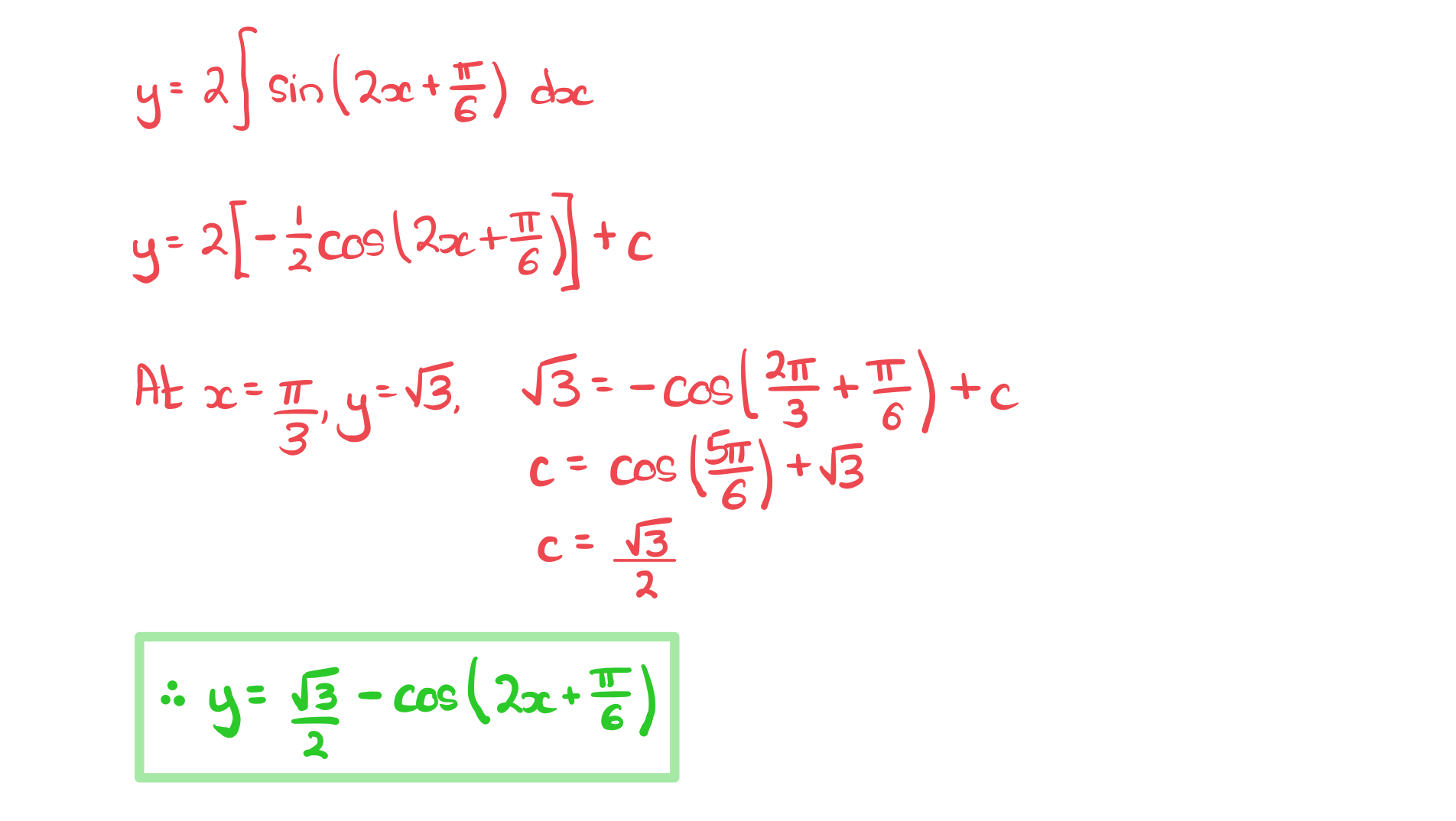
5-4-1-ib-hl-ai-aa-extraaa-we1b-soltn-

Did this video help you?

Integrating e^x & 1/x

How do I integrate exponentials and 1/x?

  • The antiderivatives involvingbold space bold e to the power of bold italic x andspace bold ln bold space bold italic x are

bold space bold integral bold space bold e to the power of bold italic x bold space bold d bold italic x bold equals bold space bold e to the power of bold italic x bold plus bold italic c

where bold italic c is the constant of integration

  • These are given in the formula booklet

  • For the linear functionbold space bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis, wherespace bold italic a andspace bold italic b are constants,

 bold space bold integral bold e to the power of bold italic a bold italic x bold italic plus bold italic b end exponent bold space bold d bold italic x bold equals bold 1 over bold italic a bold e to the power of bold italic a bold italic x bold italic plus bold italic b end exponent bold plus bold italic c

  • It follows from the last result that

 

  • which can be deduced using Reverse Chain Rule

  • With ln, it can be useful to write the constant of integration,space c, as a logarithm

    • using the laws of logarithms, the answer can be written as a single term

    • wherespace k is a constant

    • This is similar to the special case of differentiatingspace ln space left parenthesis a x plus b right parenthesis whenspace b equals 0

Examiner Tips and Tricks

  • Make sure you have a copy of the formula booklet during revision but don't try to remember everything in the formula booklet

    • However, do be familiar with the layout of the formula booklet

      • You’ll be able to quickly locate whatever you are after

      • You do not want to be searching every line of every page!

    • For formulae you think you have remembered, use the booklet to double-check

Worked Example

A curve has the gradient functionspace f apostrophe left parenthesis x right parenthesis equals fraction numerator 3 over denominator 3 x plus 2 end fraction plus straight e to the power of 4 minus x end exponent.


Given the exact value ofspace f left parenthesis 1 right parenthesis isspace ln space 10 minus straight e cubed find an expression forspace f left parenthesis x right parenthesis.

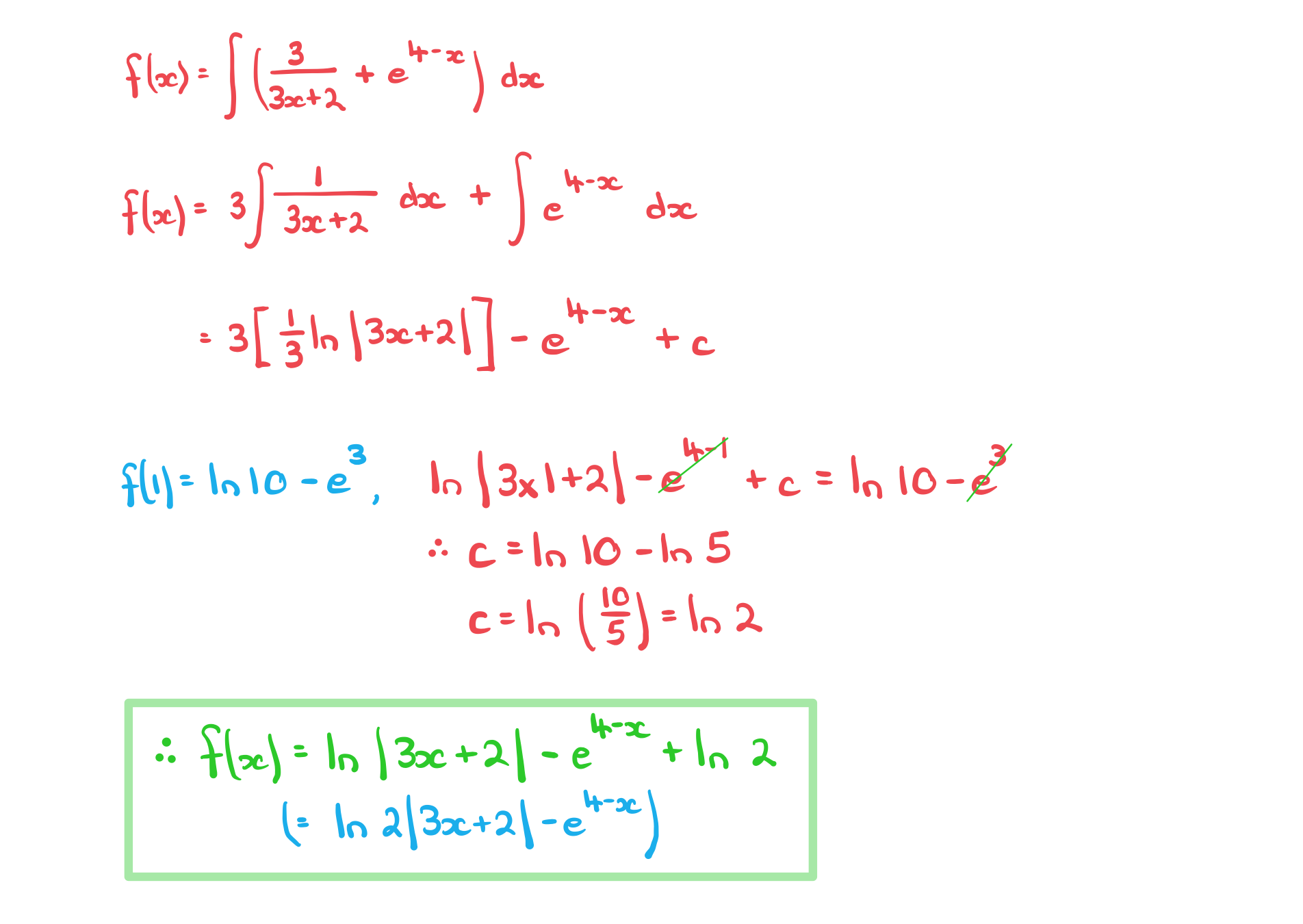
NA5HYQ75_5-4-1-ib-sl-aa-only-we2-soltn
👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourselfFlashcards

Did this page help you?

Previous:Applications of IntegrationNext:Techniques of Integration
Paul

Author: Paul

Expertise: Maths Content Creator

Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.

Download notes on Integrating Trigonometric, Exponential & Reciprocal Functions