Reverse Chain Rule (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Integrating composite functions (ax+b)
What is a composite function?
A composite function involves one function being applied after another
A composite function may be described as a “function of a function”
E.g.
First the function
is applied to
Then the function
is applied to
This Revision Note focuses on one of the functions being linear – i.e. of the form
How do I integrate linear (ax+b) functions?
A linear function (of
) is of the form
, where
and
are constants
The special cases for trigonometric functions and exponential and logarithm functions are
There is one more special case you should know
where
, in all cases, is the constant of integration
All the above can be deduced using reverse chain rule
However, recognising the patterns and knowing these results can make solutions more efficient
Examiner Tips and Tricks
The specific formulas given here are not in the exam formula booklet.
However if you don't remember them, they can all be derived using results that are in the formula booklet plus reverse chain rule.
Worked Example
Find the following integrals
a)
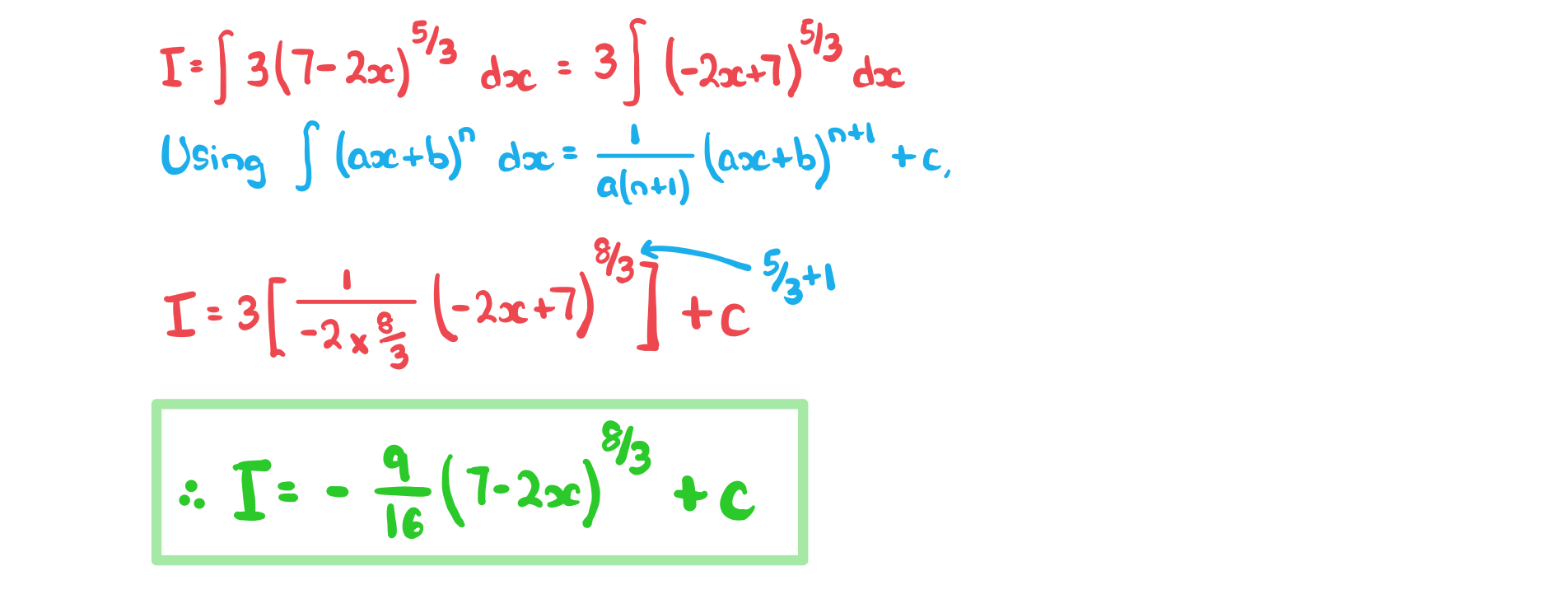
b)
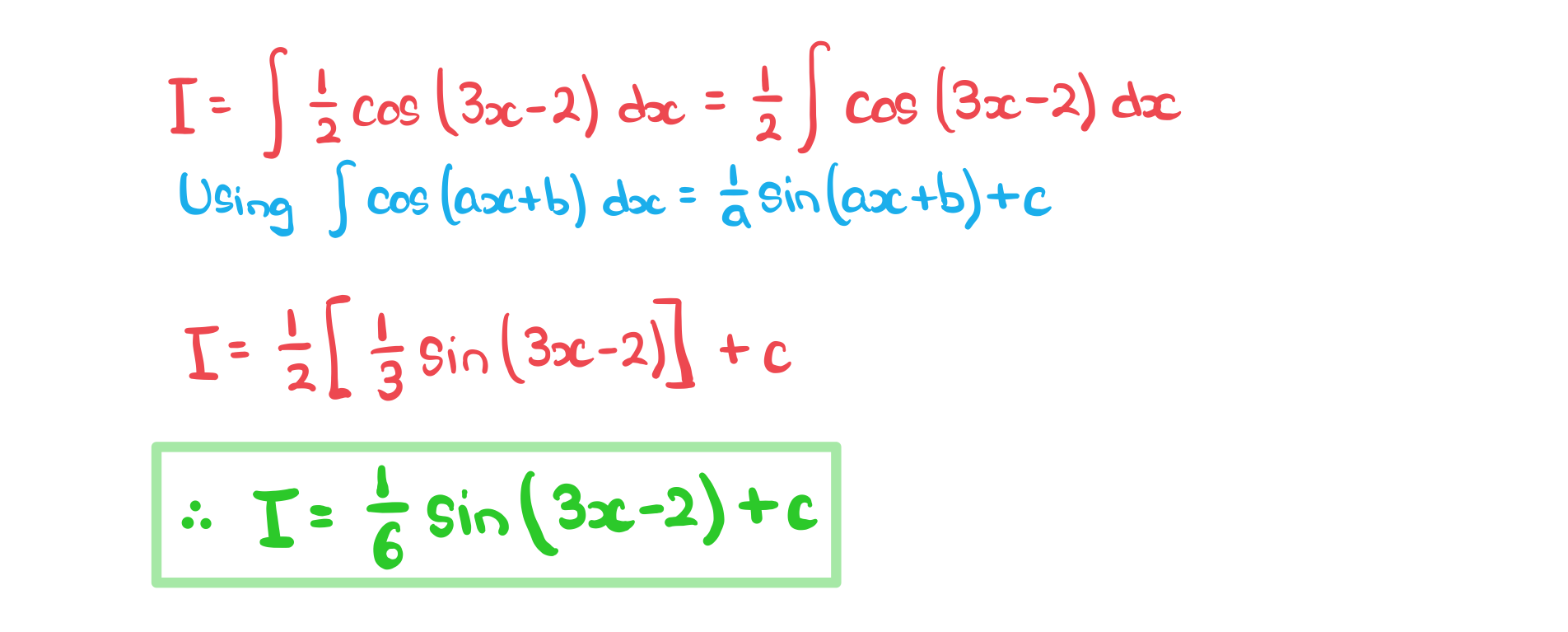
Did this video help you?
Reverse chain rule
What is reverse chain rule?
The Chain Rule is a way of differentiating composite functions made up of two (or more) functions
Reverse Chain Rule (RCR) refers to integrating by inspection
You do this by spotting that chain rule would be used in the reverse (differentiating) process
How do I know when to use reverse chain rule?
Reverse chain rule is used when we have the product of a composite function and the derivative of its secondary function
E.g.
is a composite function
is the primary (or main or 'outside') function
is the secondary (or 'inside') function
is the derivative of the secondary function
Formally, in function notation, reverse chain rule can be written in the following way
E.g.
,
, and
And
is the derivative of
, so
Therefore
Be sure also to recognise this useful instance of reverse chain rule
I.e. the numerator is the derivative of the denominator
E.g.
And the derivative of that is
Therefore
Examiner Tips and Tricks
You may need to 'adjust and compensate' to deal with any coefficients and get an integral into exact reverse chain rule form. For example:
How do I integrate using reverse chain rule?
If you can spot the patterns, the integration can be done “by inspection”
Though there may be some “adjusting and compensating” to do
A lot of the method happens mentally
This is indicated in the steps below by quote marks
STEP 1
Spot the ‘main’ function
e.g.
"the main function is
which would come from
”
STEP 2
‘Adjust and compensate’ any coefficients required in the integral
e.g. "
would differentiate to
"
“chain rule says multiply by the derivative of
, which is
”
“there is no '7' or ‘10’ in the integrand so adjust and compensate”
STEP 3
Integrate and simplify
After some practice, you may find Step 2 is not needed
Do use it on more awkward questions (negatives and fractions!)
Examiner Tips and Tricks
Before the exam, practise this until you are confident with the reverse chain rule patterns and do not need to worry about the formula or steps anymore.
You can always check your work by differentiating, if you have time. Your answer should differentiate to give the original function you were integrating.
Examiner Tips and Tricks
Reverse chain rule integrals can also always be integrated using substitution. However if you can spot the pattern and see how to 'adjust and compensate' (if necessary), then reverse chain rule is a lot quicker.
Worked Example
A curve has the gradient function.
Find an expression for.


Unlock more, it's free!
Did this page help you?