National 5PhysicsSQARevision NotesElectricityOhm’s LawCalculating Potential Difference, Current & Resistance

Calculating Potential Difference, Current & Resistance (SQA National 5 Physics): Revision Note

Exam code: X857 75

Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on

Calculating potential difference, current & resistance

  • The current, resistance and potential difference of a component in a circuit can be calculated using the relationship:

V space equals space I R

  • Where:

    • V = potential difference, measured in volts (V)

    • I = current, measured in amperes or amps (A)

    • R = resistance, measured in ohms (Ω)

  • This relationship is sometimes called Ohm's law, but only when the resistance of a component is constant

  • It can be rearranged with the help of the following relationship triangle:

Relationship triangle for voltage, current and resistance

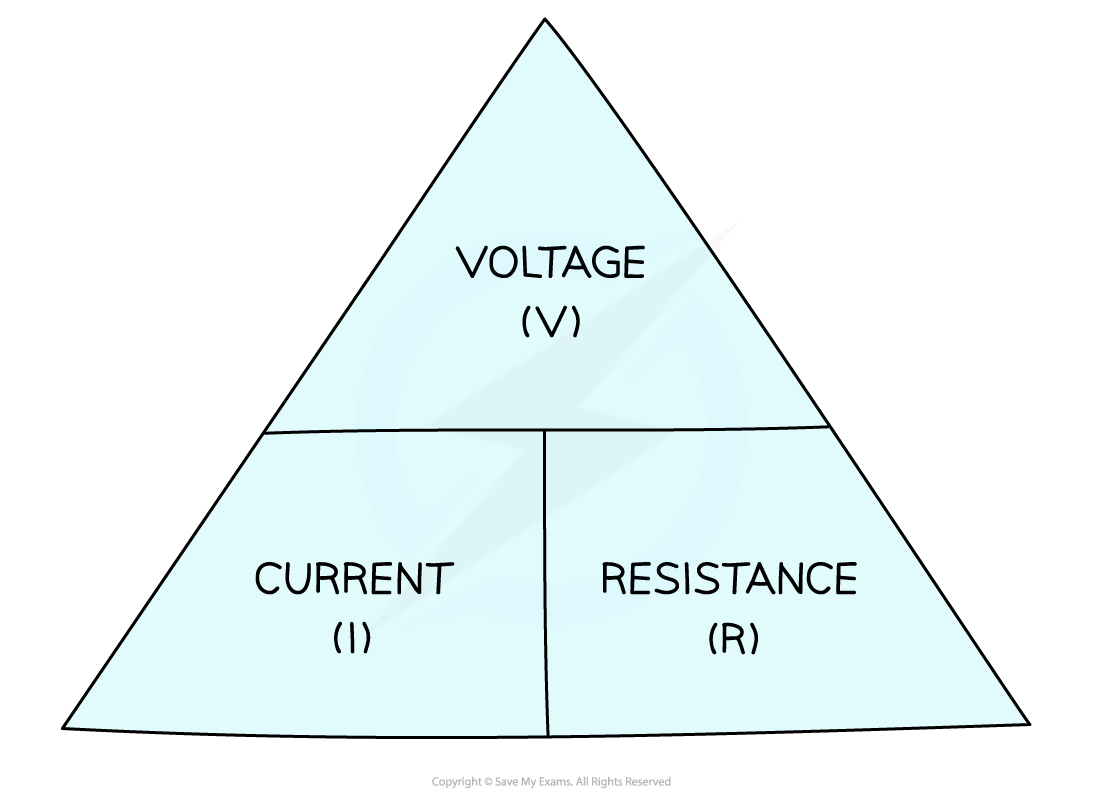
Triangle diagram with "Voltage (V)" at the top, "Current (I)" and "Resistance (R)" at the bottom, illustrating Ohm's Law.
To use a relationship triangle, simply cover up the quantity you wish calculate and the structure of the relationship is revealed

  • Check out this revision note on motion relationships if you need a reminder on how to use relationship triangles

Worked Example

A 12 Ω resistor has a current of 0.3 A flowing through it. 

Determine the potential difference across the resistor.

Answer:

Step 1: List the known quantities

  • Resistance, R space equals space 12 space straight capital omega

  • Current, I space equals space 0.3 space straight A

Step 2: Write out the relationship between potential difference, current and resistance

V space equals space I space cross times space R

Step 3: Substitute in the known values to calculate

V space equals space 0.3 space cross times space 12

V space equals space 3.6 space straight V

Potential dividers

  • When two resistors are connected in series, the potential difference across the power source is shared between them

  • A potential divider is a circuit which splits potential difference from a power source, so only a fraction goes to a component (a voltmeter, in the diagram below)

Potential divider circuit diagram

Potential divider, IGCSE & GCSE Physics revision notes

A potential divider splits the potential difference of a power source between two components

  • The potential difference across each resistor depends upon its resistance:

    • The resistor with the largest resistance will have a greater potential difference than the other one

    • If the resistance of one of the resistors is increased, it will get a greater share of the potential difference, whilst the other resistor will get a smaller share

  • If one resistor is a variable resistor, the potential difference across the other resistor can be altered

    • This means the potential difference across any component in parallel with that resistor can also be altered

Resistors as potential dividers

  • When two resistors are connected in series, the voltage of the supply is split between the resistors

    • This potential difference splits in the same ratio as the resistance of the two resistors

  • The ratio of potential differences across each resistor can be found using the following equation:

V subscript 1 over V subscript 2 space equals space R subscript 1 over R subscript 2

  • Where:

    • V subscript 1 is the potential difference across resistor 1 in volts, V

    • V subscript 2 is the potential difference across resistor 2 in volts, V

    • R subscript 1 is the resistance of resistor 1 in ohms, Ω

    • R subscript 2 is the resistance of resistor 2 in ohms, Ω

  • For the two resistors connected in series:

    • the voltage V subscript S of the supply is equal to V subscript 1 space plus space V subscript 2

    • the total resistance R is equal to R subscript 1 space plus space R subscript 2

  • Therefore, the ratio can also be written as

V subscript 2 space equals space open parentheses fraction numerator R subscript 2 over denominator R subscript 1 space plus space R subscript 2 end fraction close parentheses V subscript S

  • Where:

    • V subscript S is the potential difference of the supply in volts, V

Worked Example

The circuit is designed to light up a lamp when the input voltage exceeds a value.

When the lamp lights up, V subscript o u t end subscript is 5.3 V. 

Calculate the e.m.f. of the power source required to illuminate the lamp.

WE - potential divider question image, downloadable AS & A Level Physics revision notes

Answer:

Step 1: List the known quantities

  • Resistance of resistor 1, R subscript 1 = 12 kΩ = 12 000 Ω

  • Resistance of resistor 2, R subscript 2 = 20 kΩ = 20 000 Ω

  • Potential difference across resistor 2, V subscript 2 space equals space V subscript o u t end subscript = 5.3 V

Step 2: Recall the equation for a potential divider

R subscript 1 over R subscript 2 space equals space V subscript 1 over V subscript 2

Step 3: Substitute the known quantities and determine the potential difference across resistor 1

fraction numerator 12 space 000 over denominator 20 space 000 end fraction space equals space fraction numerator V subscript 1 over denominator 5.3 end fraction

V subscript 1 space equals space 3.18 space straight V

Step 4: Determine the e.m.f. of the power source, V subscript i n end subscript

V subscript i n end subscript space equals space V subscript 1 space plus space V subscript 2

V subscript i n end subscript space equals space 3.18 space plus space 5.3 space equals space 8.48 space straight V

  • The e.m.f. of the power source when the lamp illuminates is 8.5 V to 2 significant figures

Examiner Tips and Tricks

When thinking about potential dividers, remember that the higher the resistance the more energy it will take to 'push the current through' and therefore the higher the potential difference.

This means that if a component (often shown as a voltmeter in questions) needs to be switched on by a change such as increased light or temperature, then the resistor it is in parallel with needs to become larger compared to the other resistor.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Voltage-Current (V-I) GraphsNext:Resistance & Temperature
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Caroline Carroll

    Reviewer: Caroline Carroll

    Expertise: Physics & Chemistry Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.