State two necessary conditions for a stationary wave to be set up on a string.
State the principle of superposition.
A stationary wave is made up of nodes and anti–nodes.
Define what is meant by a:
(i) node
(ii) anti–node
Figure 1 shows a stationary wave on a string fixed at both ends.
Figure 1
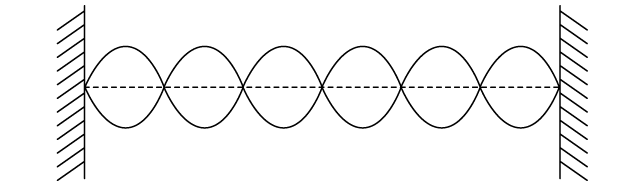
Draw on Figure 1 and label the nodes (N) and anti–nodes (A).
Was this exam question helpful?






















