Vector Equations of Lines (DP IB Analysis & Approaches (AA): HL): Exam Questions

Point  has coordinates  and the line  is defined by the equations:

Point  lies on the line such that  is perpendicular to .

Find the coordinates of point .

Hence find the shortest distance from A to the line .

Find the vector equation of the line  with Cartesian equations 

A second line  runs parallel to  and passes through the points  and .

Find the values of  and 

Hence write down the equation of line in Cartesian form.

A line  passes through the points  and and lies normal to the vector . 

Find the vector equation of  .

Find the obtuse angle formed by the two lines  and defined by the equations:

Consider the skew lines and  as defined by:

Find a vector that is perpendicular to both lines.

Hence find the shortest distance between the two lines.

Consider the lines  and defined by the equations:

Given that   and  are coincident, find the value of  and .

Two spaceships , in a 3D virtual reality game, are moving such that their positions relative to a fixed point  at time seconds, , are defined by the position vectors  and  respectively.

Show that the two spaceships are on course to collide at point  and write down the coordinates of .

Spaceship  reduces its velocity such that its position vector is now given by

Show that spaceship is still travelling in its original direction.

Show that the distance between the two spaceships can be written as

Hence find the distance between the two spaceships when spaceship  is at .

A car is moving with constant velocity along the line with equation A bird is perched at the point  and at , starts to fly at a constant velocity in the direction of the vector .

All distances are measured in metres and time in seconds. The base vectors  and  represent due east and due west respectively and the base vector  points upwards.

Verify that the bird does not collide with the car.

Show that at some point in time the bird will be directly above the car and state the time at which this occurs.

Hence find the distance between the bird and the car at that time.

Consider the triangle ABC. The points A, B and C have coordinates  and  respectively.  A vector equation of the line that passes through point  and the midpoint of  is  

Find the value of .

Find the vector equation of the line that passes through point B and the midpoint of [AC].

The two lines intersect inside the triangle at point X.

Show that the area of  is   the area of triangle .

In the magical kingdom of Cartesia, all positions are measured relative to the ancient stone of power known as the Origin. This reference system corresponds to the standard  coordinate system used in mathematics, as shown in the diagram below.

Prince Vector, son of King Prime of Cartesia, needs to fly on his magical unicorn from the top of the Mystic Pedestal all the way to Cloud City, on an urgent rescue mission. 

The Mystic Pedestal is 14 kilometres west and 8 kilometres north of the Origin, and its top is one kilometre up from the level of the Origin. Cloud City is 11 kilometres east and 13 kilometres north of the Origin, and it is 11 kilometres up from the level of the Origin. 

Since there is not much time, the prince must fly directly from the top of the Mystic Pedestal to Cloud City. Unfortunately, the unicorn’s magic levels are low. In order for the unicorn to recharge it must pass within 12 kilometres of the Origin during the flight, and must do this before reaching the halfway point between the Mystic Pedestal and Cloud City. If the unicorn does not recharge before this point then it and the prince will crash into the barren wastes and the kingdom will perish. 

Using a vector method, determine whether or not the prince will reach Cloud City successfully. Use clear mathematical workings to justify your answer.

The line  has equation  and point A has coordinates . Given that the shortest distance between point A and the line is units, find , where .

A line  has the equation  and intersects the line  with equation at point P, when .

A third line runs parallel to  and also intersects  at point .  

Find the parametric equations of .

Find the distance .

Consider the two intersecting lines  and  defined by the equations:

Given that the angle between  and  is rad, correct to 4 significant figures, find the value of , where .

Find the value of , giving your answer correct to 3 significant figures.

Consider the two lines  and , where passes through the points  and and is defined by the Cartesian equations  

Find the shortest distance between the two lines.

Consider the line as defined by the equation . 

A point  lies at a distance of units perpendicular from a point on . 

Find all possible coordinates of .

Given that , write down the set of parametric equations that defines the line that passes through points  and .

A third line  is defined by the equations .

Determine the relationship between lines  and .

A wheelchair ramp is required to provide access to a building with a door that is located 22 cm above ground level.  The maximum angle that a ramp must be from the horizontal is 4.8°.

Calculate the minimum horizontal distance that the ramp must extend out.

The wheelchair ramp is supported by a steel frame.  A cross section of the ramp can be seen in the diagram below.  A metal strut joins M, the midpoint of [AC], to a point X on the line [AB]. [AB]. XM=11.1 cm and =90°.  

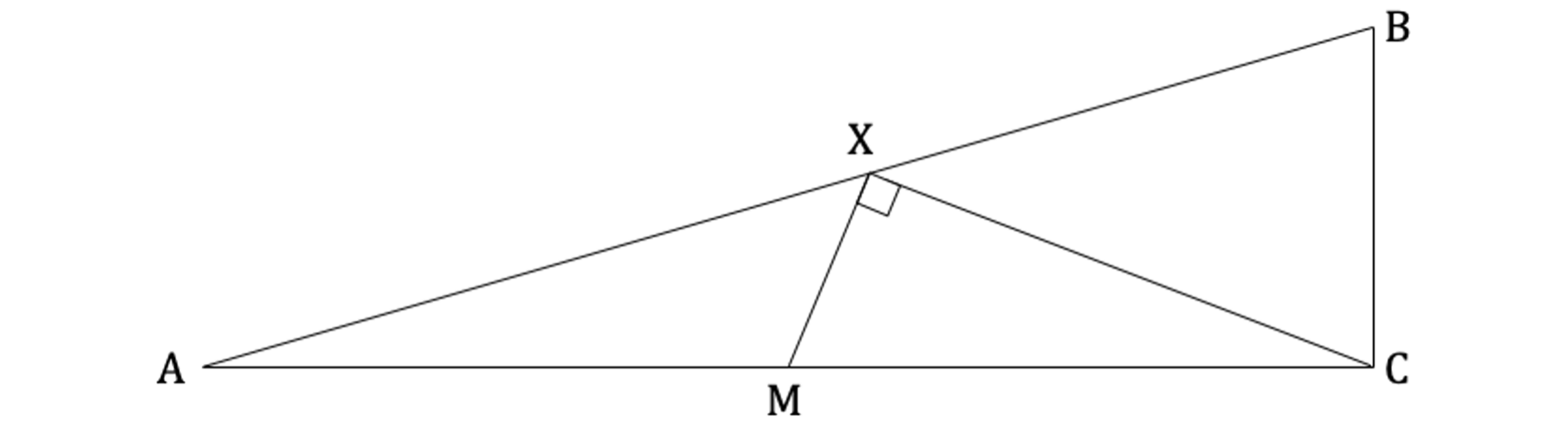
Using the horizontal distance found in part (a) and assuming that point A is at the origin, use a vector method to calculate the length XB.

Two drones X and Y are being flown over an area of rainforest to look for signs of illegal logging. Their positions relative to the observation centre, are given by

  and 

at time  minutes after take-off, . All distances are in metres.

Verify that the two drones will not collide.

Find the shortest distance between the two drones and the time at which it occurs.

A third drone Z begins its flight at  and its position relative to the observation centre is given by  

Each drone can observe a circular area of ground,   such that  where  is the height of the drone above the ground in metres.

Show that the area of ground that can be observed by drone Z five minutes after it takes off overlaps with the area of ground that can be observed by drone Y at that time.

Consider the tetrahedron ABCD, where A(3, 5, 8), B(-2, 3, 2), C(5, -1, 3) and D(-3, 0, 1). M is the midpoint of the line BC and point P lies along the line DM.

Given that the volume of the tetrahedron ABCP is of the volume of the tetrahedron ABCD, find the Cartesian equations of the line going through points A and P.

X is the midpoint of [AD].

Find the coordinates of the point of intersection between the line found in part (a) and the line going through [MX].

A car is moving at a constant speed of 15 ms^-1 in the direction parallel to the vector  Two birds are perched at points  and . 

At , the car is located at  and the bird at point A starts to fly at a constant velocity of   ms^-1. The bird at point B begins to fly at a constant velocity in the direction of the vector  when . 

When bird A reaches the position of , both birds and the car lie in a straight line.

Find the equation of the line along which the birds and car lie.

Find the speed at which bird B is travelling.