National 5MathsSQAApplications of MathematicsRevision NotesGeometric SkillsGradients & PythagorasGradient

Gradient (SQA National 5 Applications of Mathematics): Revision Note

Exam code: X844 75

Dan Finlay

Written by: Dan Finlay

Reviewed by: Roger B

Updated on

Gradient using distances

What is the gradient of a line?

  • The gradient is a measure of how steep a straight line is

  • A gradient of 3 means:

    • For every 1 unit to the right, go up by 3

  • A gradient of 3 is steeper than 2

How do I find the gradient of a line using distances?

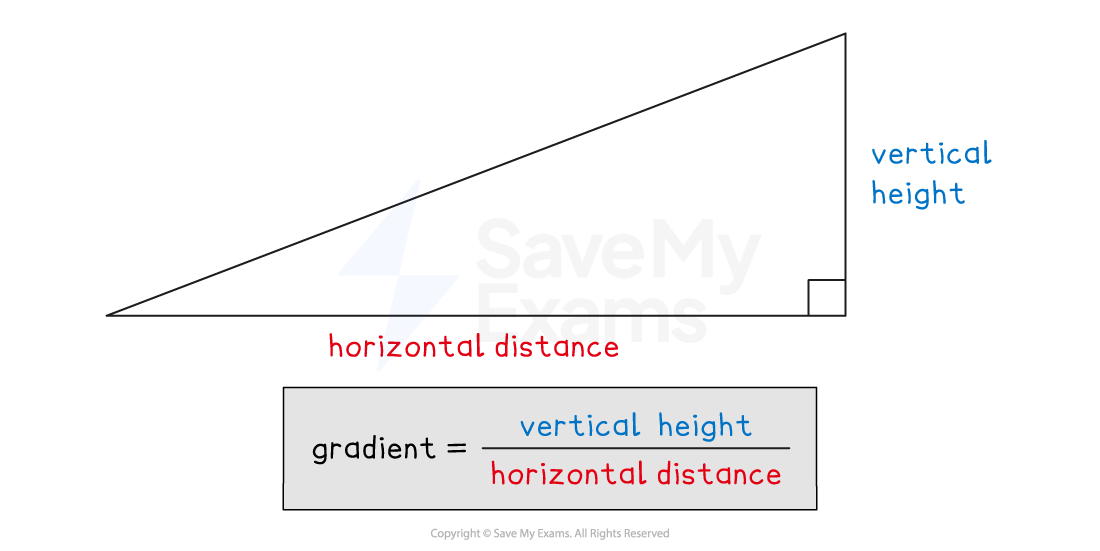
  • Identify a right-angled triangle using the line as the hypotenuse

  • Find the horizontal distance of the line

  • Find the vertical height of the line

  • The formula is gradient equals fraction numerator vertical space height over denominator horizontal space distance end fraction

    • You are given this formula in your exam

Right-angled triangle illustrating gradient, with labels for vertical height and horizontal distance. Gradient formula shown as vertical height over horizontal distance.

Examiner Tips and Tricks

Make sure that the horizontal distance and the vertical height are measured in the same units.

Worked Example

The diagram shows a child's slide.

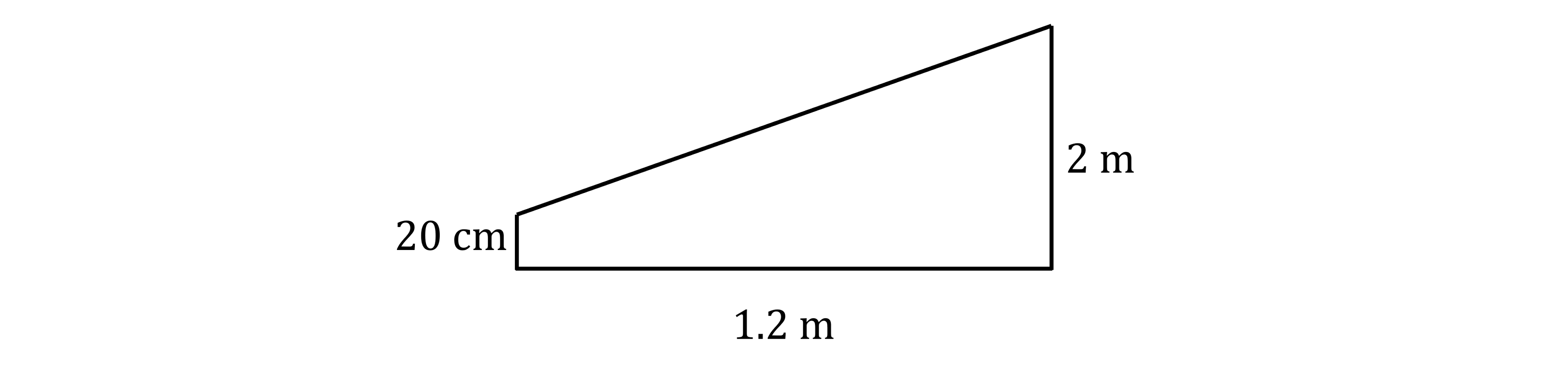
A right-angled trapezium with the left vertical side 20 cm, right vertical side 2 m, and a horizontal base 1.2 m.

The start of the slide is 2 metres above the ground. The end of the slide is 20 centimetres above the ground.

Calculate the gradient of the slide.

Answer:

Convert all lengths to centimetres

  • Multiply metres by 100

1.2 m = 120 cm

2 m = 200 cm

Identify the right-angled triangle

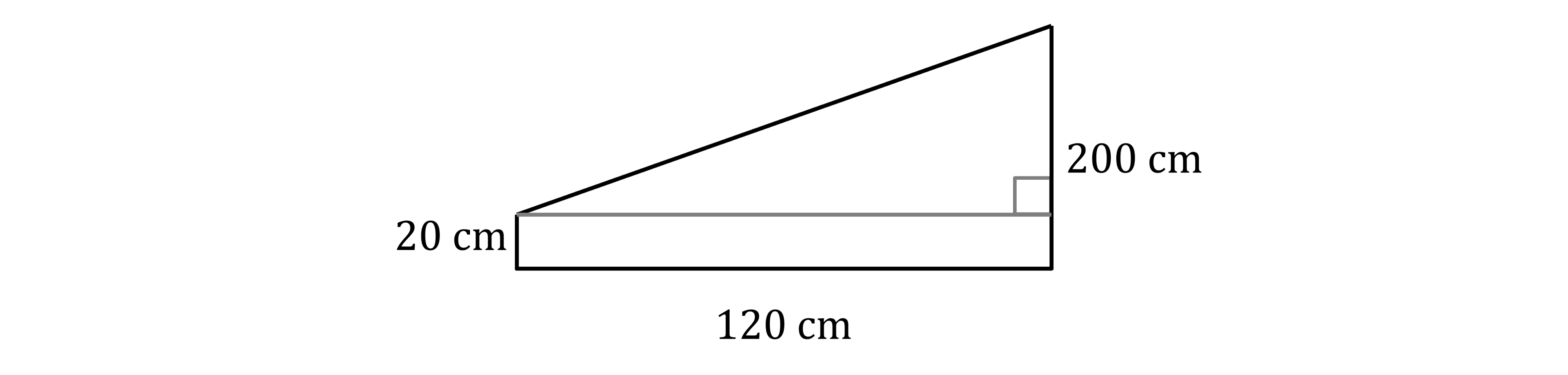
Diagram of a right-angled triangle on top of a 120 cm by 20 cm rectangle. Total height of triangle is 200 cm.

Find the vertical height of the triangle

  • Subtract the height of the end from the height of the start

200 cm - 20 cm = 180 cm

Use gradient equals fraction numerator vertical space height over denominator horizontal space distance end fraction

180 over 120 equals 1.5

Gradient = 1.5

Gradient using coordinates

How do I find the gradient of a line using coordinates?

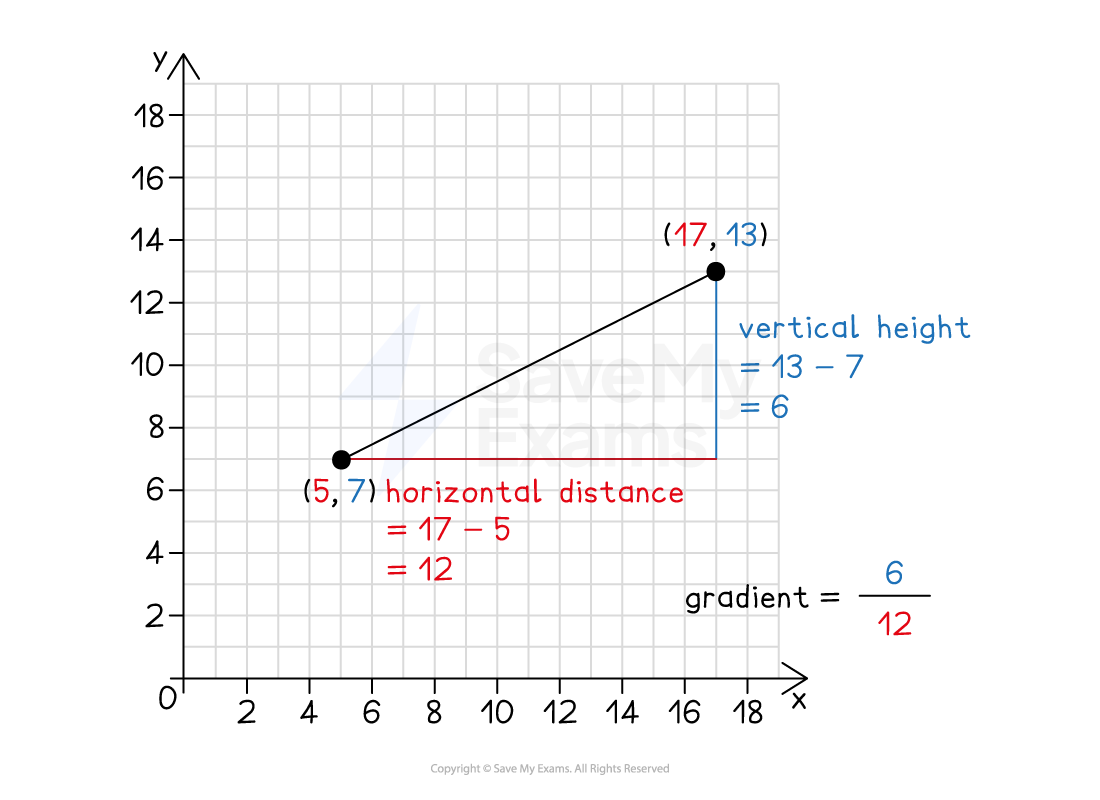
  • Join the two points together with a straight line and form a right-angled triangle underneath

  • Find the horizontal distance between the x coordinates

  • Find the vertical height between the y coordinates

  • Use the formula gradient equals fraction numerator vertical space height over denominator horizontal space distance end fraction

Graph showing a line between points (5, 7) and (17, 13) with horizontal distance 12, vertical height 6, and gradient calculation as 6/12.
Example of finding the gradient using coordinates

Worked Example

Jerry draws a line of best fit on a scattergraph. The line goes through the points open parentheses 4 comma space 11 close parentheses and open parentheses 12 comma space 17 close parentheses.

Calculate the gradient of the line of best fit.

Answer:

Sketch the two points and draw a right-angled triangle

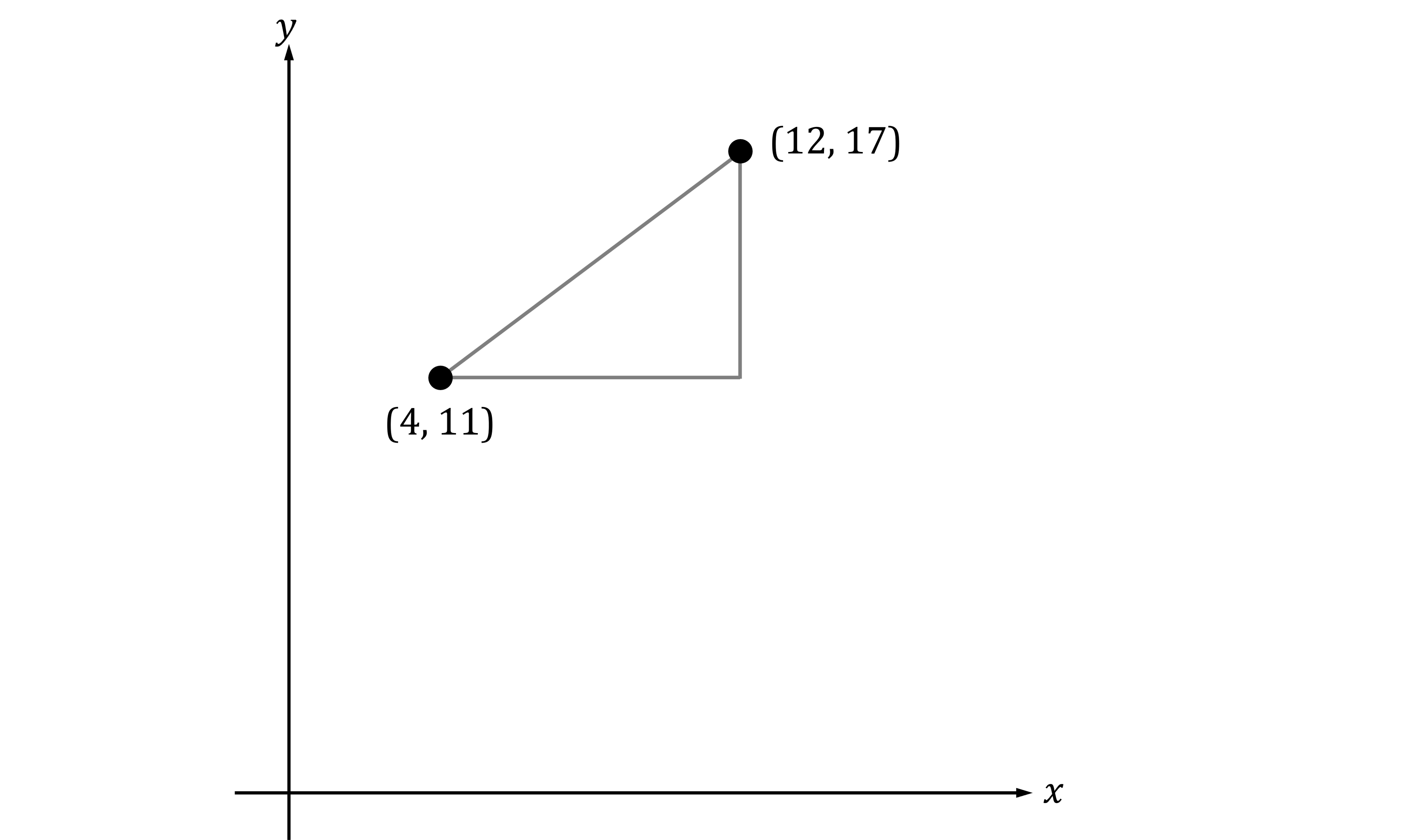
Graph with a right triangle on a coordinate plane. Points are labelled (4, 11) and (12, 17). The triangle is formed with axes as perpendicular sides.

Find the horizontal distance using the x coordinates

12 minus 4 equals 8

Find the vertical height using the y coordinates

17 minus 11 equals 6

Use the formula is gradient equals fraction numerator vertical space height over denominator horizontal space distance end fraction

6 over 8 equals 0.75

Gradient = 0.75

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Reading ScalesNext:Pythagoras' Theorem
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Roger B

    Reviewer: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.