Pythagoras' Theorem (SQA National 5 Applications of Mathematics): Revision Note
Exam code: X844 75
Pythagoras' theorem
What is Pythagoras' theorem?
Pythagoras' theorem is a formula that links the lengths of the three sides of a right-angled triangle
The longest side of a right-angled triangle is called the hypotenuse
The hypotenuse will always be the side opposite the right angle
Pythagoras' theorem states that
is the length of the hypotenuse
and
are the lengths of the two shorter sides
It does not matter which is labelled
and which is labelled

How do I use Pythagoras’ theorem to find the length of the hypotenuse?
To find the length of the hypotenuse
Square the lengths of the two shorter sides
Add these two numbers together
Take the positive square root
How do I use Pythagoras’ theorem to find the length of a shorter side?
To find the length of a shorter side
Square the lengths of the hypotenuse and the other shorter side
Subtract these numbers to find the difference
Take the positive square root
How do I use Pythagoras’ theorem in multi-step problems?
You will be expected to use Pythagoras' theorem in multi-step problems such as
finding perimeters and areas
finding lengths of compound shapes involving two right-angled triangles
finding diameters of circles
finding the perpendicular height of an isosceles triangle
The key steps for any problem are:
identify a right-angled triangle where you know the lengths of two of the sides
you might need to draw a line to split a shape into two right-angled triangles
use the theorem to find the third side of the triangle
use the length to solve the problem
Examiner Tips and Tricks
In questions with multiple steps, do not round until the very end of the question.
Worked Example
Two ramps are placed back-to-back as shown in the diagram below.
The first ramp has a slope length of 12 metres and covers a horizontal distance of 9 m.
The two ramps together cover a horizontal distance of 22 metres.
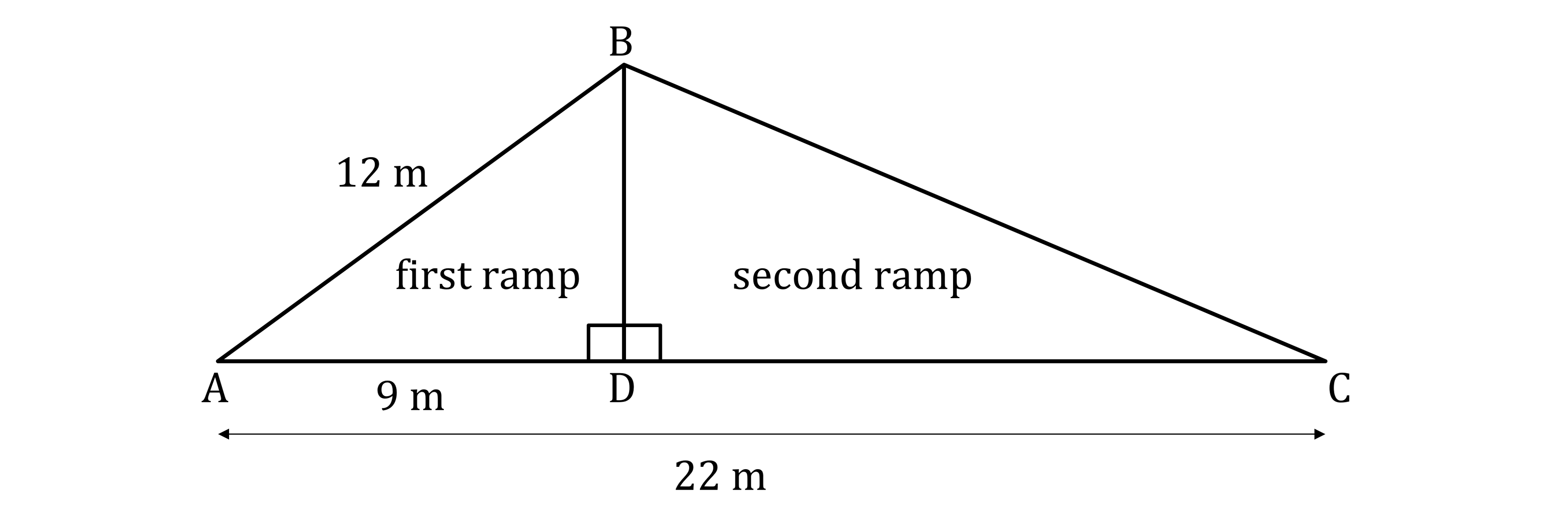
Find the length of the slope of the second ramp. Give your answer in metres correct to 1 decimal place.
Answer:
Look at the first ramp
the hypotenuse is 12 m
one of the other sides is 9 m
Use Pythagoras' theorem to find the length of the third side
square the other two lengths
find the difference because the third length is not the hypotenuse
take the square root and do not round
Look at the second ramp
find the horizontal distance by subtracting the horizontal distance of the first ramp from the total horizontal distance
the length of the other side is the same as the first ramp, 7.937... m
Use Pythagoras' theorem to find the length of the third side
square the other two lengths
use the answer button on your calculator for 7.937...
add together because the third length is the hypotenuse
take the square root
Round to 1 decimal place
15.2 m

Unlock more, it's free!
Was this revision note helpful?
