National 5MathsSQAApplications of MathematicsRevision NotesGeometric SkillsPerimeter & AreaArea of Standard Shapes

Area of Standard Shapes (SQA National 5 Applications of Mathematics): Revision Note

Exam code: X844 75

Dan Finlay

Written by: Dan Finlay

Reviewed by: Roger B

Updated on

Area of rectangles, triangles and circles

How do I find the area of a rectangle?

  • The formula for the area of a rectangle is A equals b h

    • Multiply together the base and the height

Rectangle diagram with labelled base and height. The formula for area, A = b × h, is shown below the rectangle.
Area of a rectangle

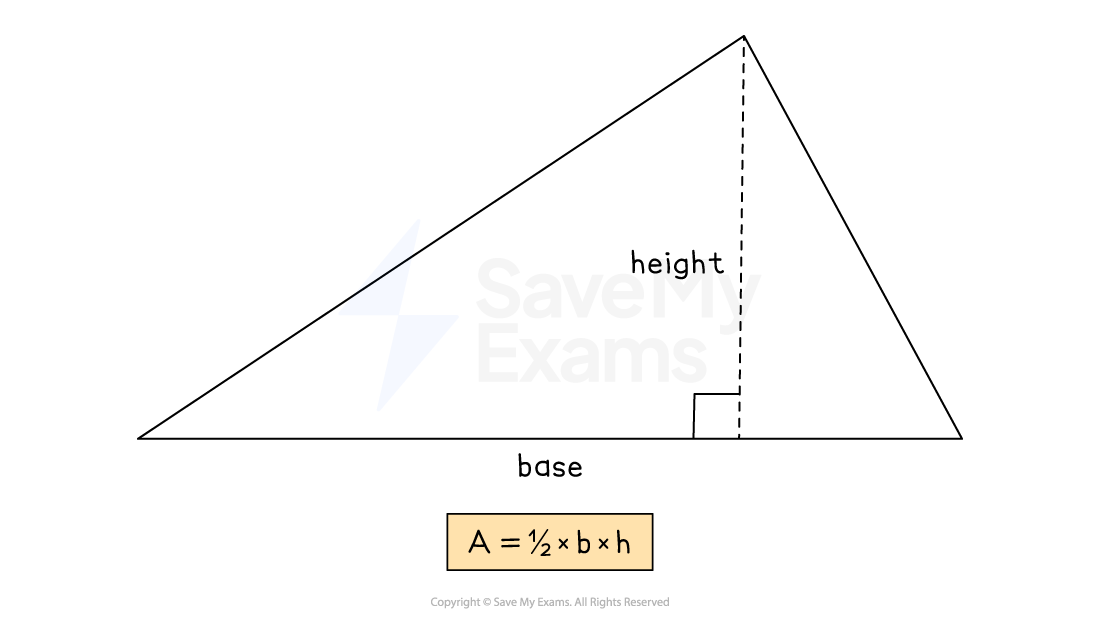
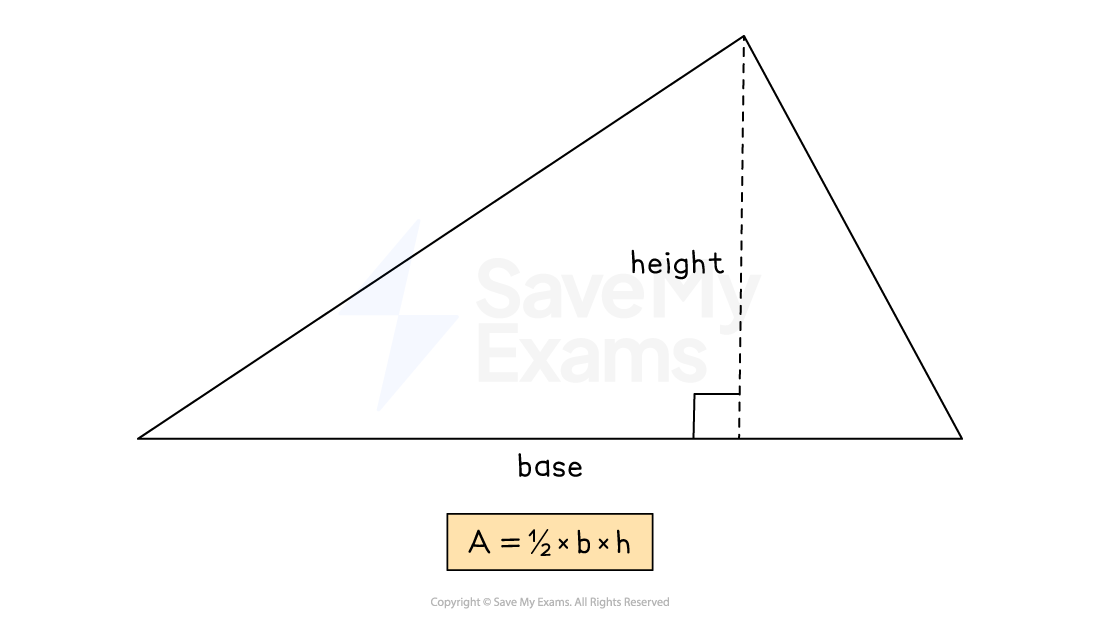
How do I find the area of a triangle?

  • The formula for the area of a triangle is A equals 1 half b h

    • Multiply together the base and the perpendicular height

    • Halve the answer

  • The perpendicular height may not be the length of one of the sides of the triangle

Triangle diagram with base and height labelled. Equation below: Area equals half times base times height.
Area of a triangle

Examiner Tips and Tricks

You might have to use Pythagoras' theorem to find the perpendicular height.

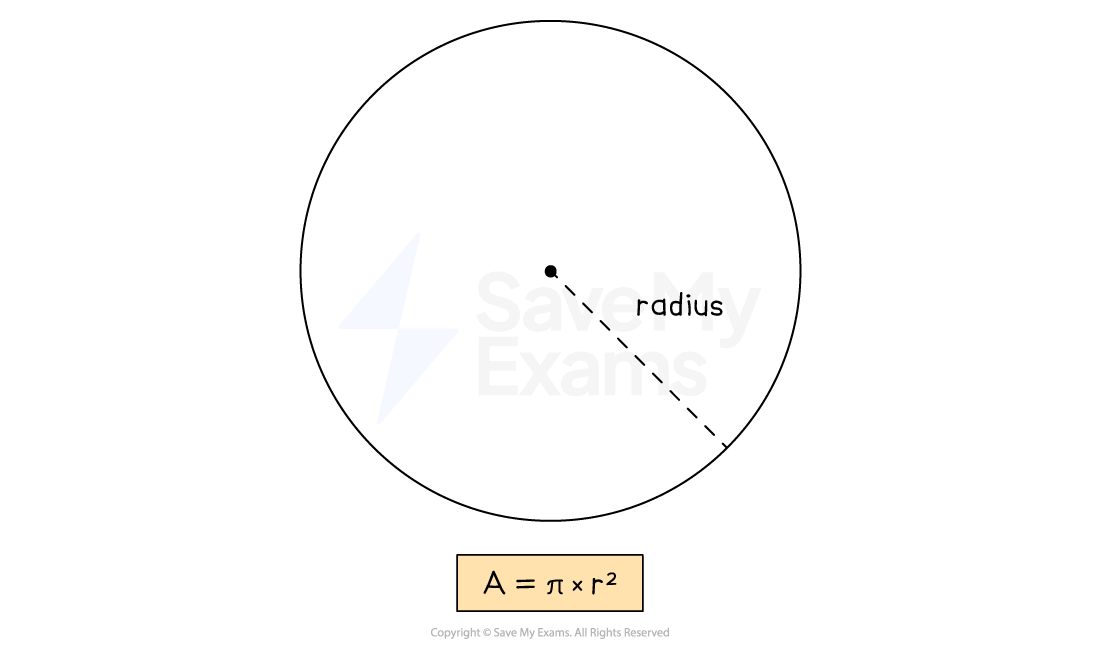
How do I find the area of a circle?

  • The formula for the area of a circle is A equals pi r squared

    • Identify the radius

      • This is half the length of the diameter

    • Square the radius

    • Multiply the radius squared by π

Diagram of a circle with a dotted line labelled "radius" from the centre to the edge, and the area formula \(A = \pi r^2\) shown below.
Area of a circle

Examiner Tips and Tricks

You are given this formula in the exam.

Worked Example

Chrissy is deciding between two shapes for her new logo. One is a circle with a diameter of 8 cm. The other is an isosceles triangle with dimensions as shown below.

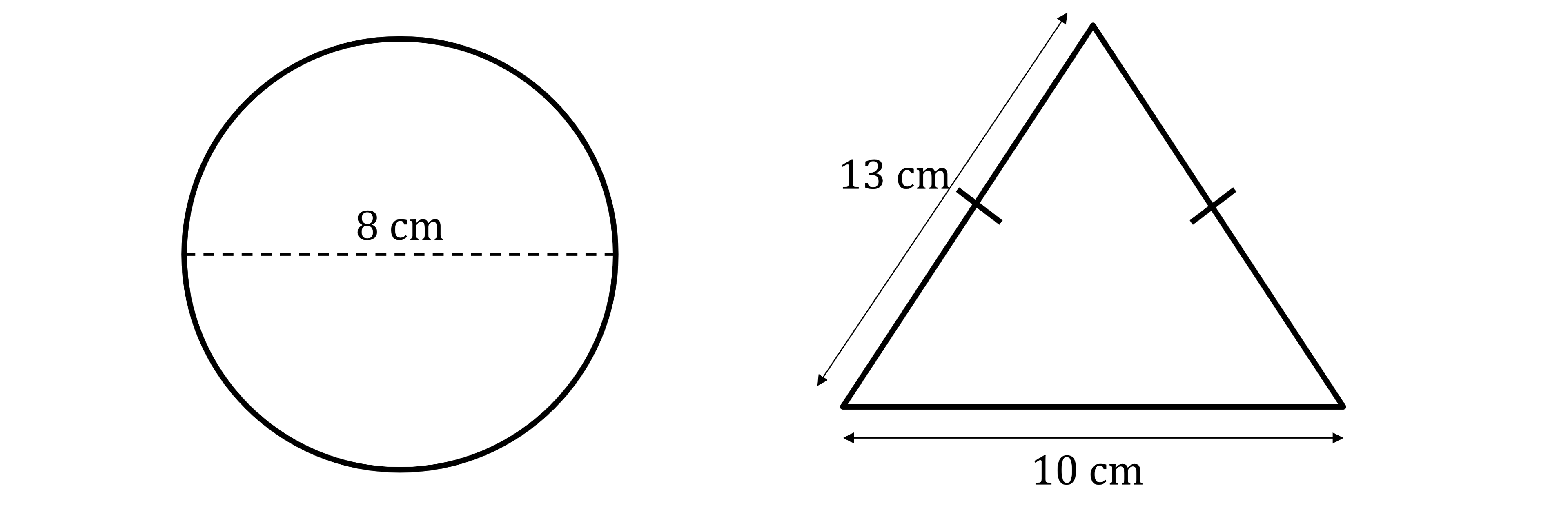
A circle with a 8 cm diameter and an isosceles triangle with 10 cm base and 13 cm equal sides, both labelled with dimensions.

Chrissy wants to choose the shape with the greatest area. Which shape should Chrissy choose?

Answer:

Find the area of both shapes

Circle

Halve the diameter to find the radius

r equals 8 space cm divided by 2 equals 4 space cm

Use A equals pi r squared

pi cross times 4 squared equals 50.26...

Triangle

Use Pythagoras' theorem to find the perpendicular height

  • Halve the base

  • Subtract the squares as you are finding a shorter side

table row cell 13 squared minus 5 squared end cell equals 144 row cell square root of 144 end cell equals 12 end table

Use A equals 1 half b h

1 half cross times 10 cross times 12 equals 60

Compare the areas and choose the shape with the greatest area

50.26... < 60

Triangle

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Perimeter & CircumferenceNext:Area of Composite Shapes
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Roger B

    Reviewer: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.