National 5MathsSQAApplications of MathematicsRevision NotesGraphical Data, Probability & Statistics SkillsProbabilitySample Space Diagrams

Sample Space Diagrams (SQA National 5 Applications of Mathematics): Revision Note

Exam code: X844 75

Dan Finlay

Written by: Dan Finlay

Reviewed by: Roger B

Updated on

Sample space diagrams

What are sample space diagrams?

  • A sample space diagram displays all the possible outcomes of an experiment

  • It can be a list or table

  • For example, consider rolling two fair dice each numbered 1 to 6 and adding together the numbers

    • A two-way table is suitable for the sample space diagram

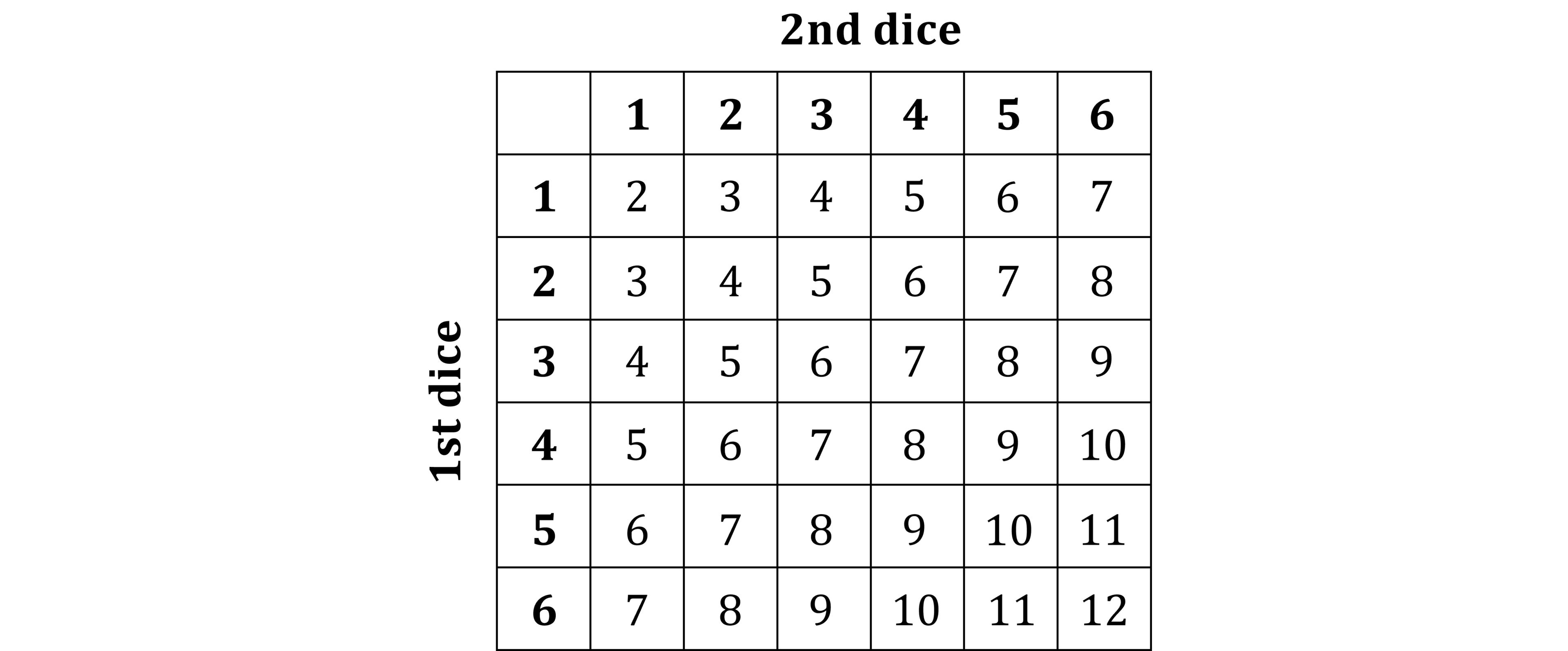
Possibility diagram for the sum of scores of two dice
All the outcomes when adding the numbers on two dice together

How do I calculate probabilities using a sample space diagram?

  • STEP 1
    Draw or complete a sample space diagram

    • e.g. by adding together the numbers on the dice in the example above

  • STEP 2
    Count the total number of possible outcomes

    • You can multiply two numbers together if the diagram is a table

      • e.g. there are 6 × 6 = 36 possible outcomes when rolling two dice

  • STEP 3
    Identify and count the outcomes which satisfy the event

    • You can circle or underline them in your diagram

  • STEP 4
    Form a fraction for the probability using fraction numerator Total space number space of space outcomes space for space the space event over denominator Total space number space of space outcomes end fraction 

Examiner Tips and Tricks

Tables can be used whenever two experiments occur. For example, picking a day out the week at random and rolling a dice. You can still draw a 7 × 6 table. You can identify the outcomes in this table that satisfy the given event by ticking the boxes in the table.

Worked Example

Lila runs a game stall at a funfair.

The game involves spinning two spinners and letting them come to rest.

The spinners are fair and are shown below.

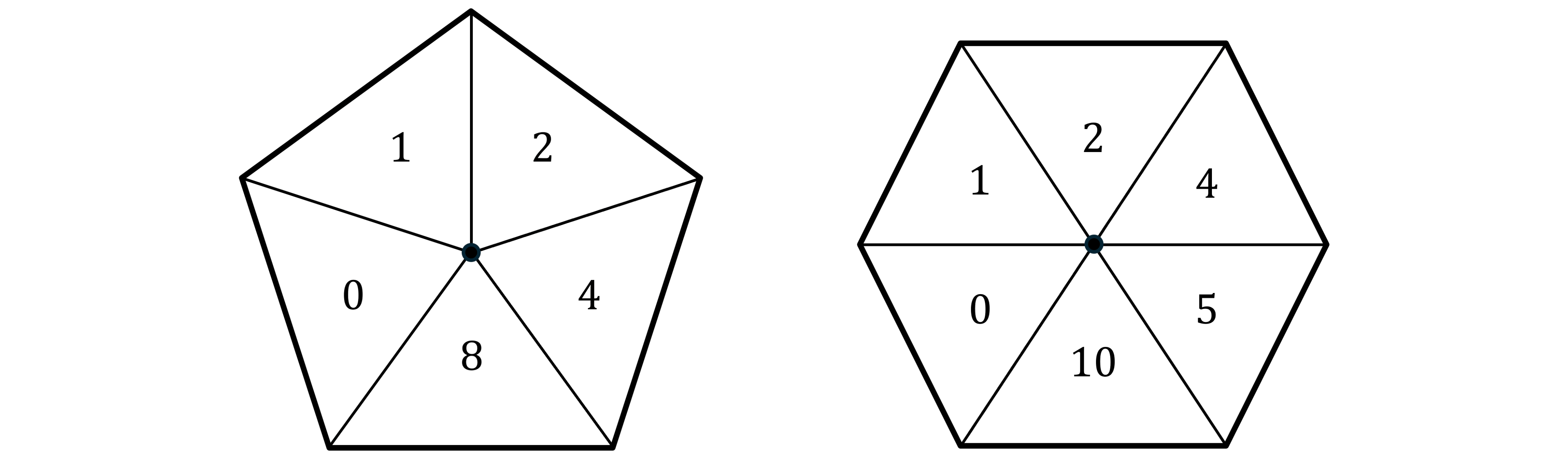
Two geometric shapes: a divided pentagon with numbers 0, 1, 2, 4, 8, and a divided hexagon with 0, 1, 2, 4, 5, 10, both centred with lines.

The numbers on which the spinners come to rest are multiplied together.

To win a prize the answer to this multiplication must be greater than 10.

Calculate the probability of winning a prize.

Answer:

Multiply all the different possibilities together

  • Draw a two-way-table

×

0

1

2

4

8

0

0

0

0

0

0

1

0

1

2

4

8

2

0

2

4

8

16

4

0

4

8

16

32

5

0

5

10

20

40

10

0

10

20

40

80

Count the total number of outcomes

5 cross times 6 equals 30

Identify the numbers that are greater than 10

×

0

1

2

4

8

0

0

0

0

0

0

1

0

1

2

4

8

2

0

2

4

8

16

4

0

4

8

16

32

5

0

5

10

20

40

10

0

10

20

40

80

8 are greater than 10

Write the probability as a fraction

8 over 30

You can simplify

4 over 15

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Probability of EventsNext:Expected Frequency
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Roger B

    Reviewer: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.