National 5MathsSQAApplications of MathematicsRevision NotesMeasurement SkillsScale Drawings & BearingsNavigation Courses

Navigation Courses (SQA National 5 Applications of Mathematics): Revision Note

Exam code: X844 75

Dan Finlay

Written by: Dan Finlay

Reviewed by: Roger B

Updated on

What is a navigation course?

  • A navigation course is a journey starting at one destination and ending on another

  • Questions involve scale drawings and bearings

Examiner Tips and Tricks

Most exam questions involve two journeys. The question will give you space to draw your navigation course, with the starting point with a north line drawn ready for you.

How do I draw a navigation course?

First journey

  • Convert the actual distance of the first journey into a distance to draw using the scale

  • Measure the given bearing starting from the starting destination

    • Measure from the north line

  • Measure the distance in that direction

  • Put a cross and label that destination

Second journey

  • Draw a north line at the current destination

  • Repeat the steps above for the second journey

  • Draw a straight line from the starting destination to the final destination

    • You can use this to find:

      • the distance between them

      • the bearing from the starting destination to the final destination

Worked Example

Julie is travelling between three towns.

  • Julie leaves Town A and travels on a bearing of 055° for 17.5 km to Town B.

  • Julie then travels on a bearing of 170° for 31.5 km to Town C.

(a) Construct a scale drawing to illustrate the route.

Use a scale of 1 cm : 5 km

Arrow pointing north with "N" at the top and "Town A" at the bottom, indicating direction towards Town A. All text is centred above or below the arrow.

(b) Julie then returns to Town A.

Use the scale drawing to determine the bearing and distance of Town A from Town C.

Answer:

(a)

Use the scale to find the scaled lengths for 17.5 km and 31.5 km

17.5 divided by 5 equals 3.5

31.5 divided by 5 equals 6.3

Draw a 3.5 cm line on a bearing of 055° from Town A and label it as "Town B"

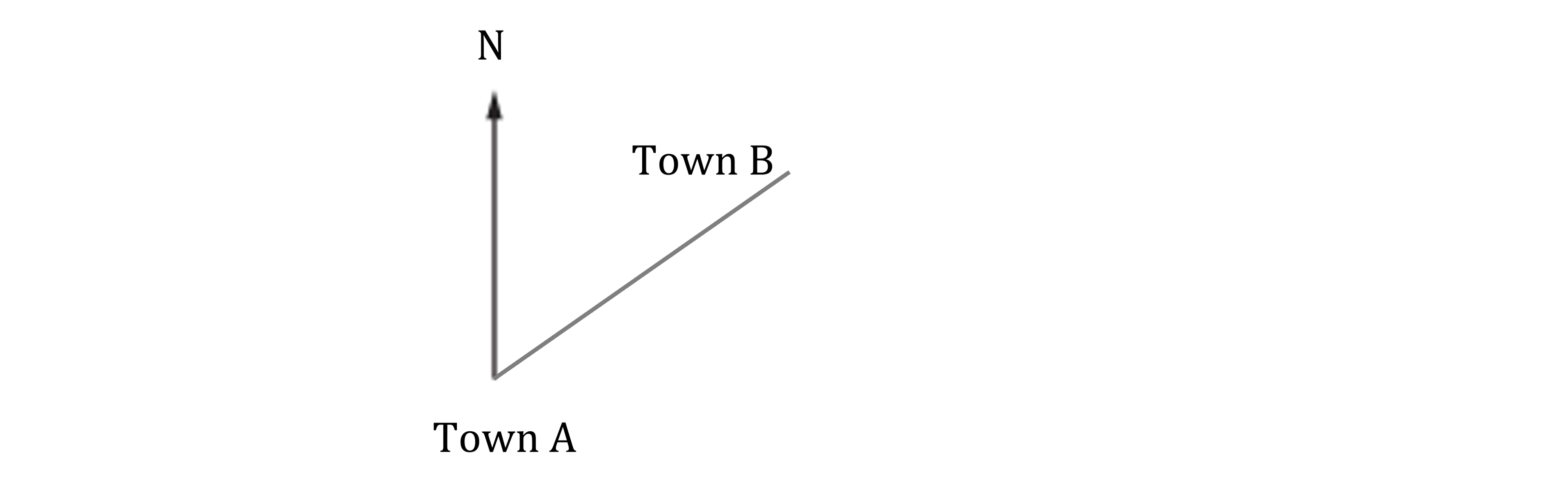
Diagram showing Town A at the base of a north-pointing arrow, with Town B to the northeast at an angle.

Draw a 6.3 cm line on a bearing of 170° from Town B and label it as "Town C"

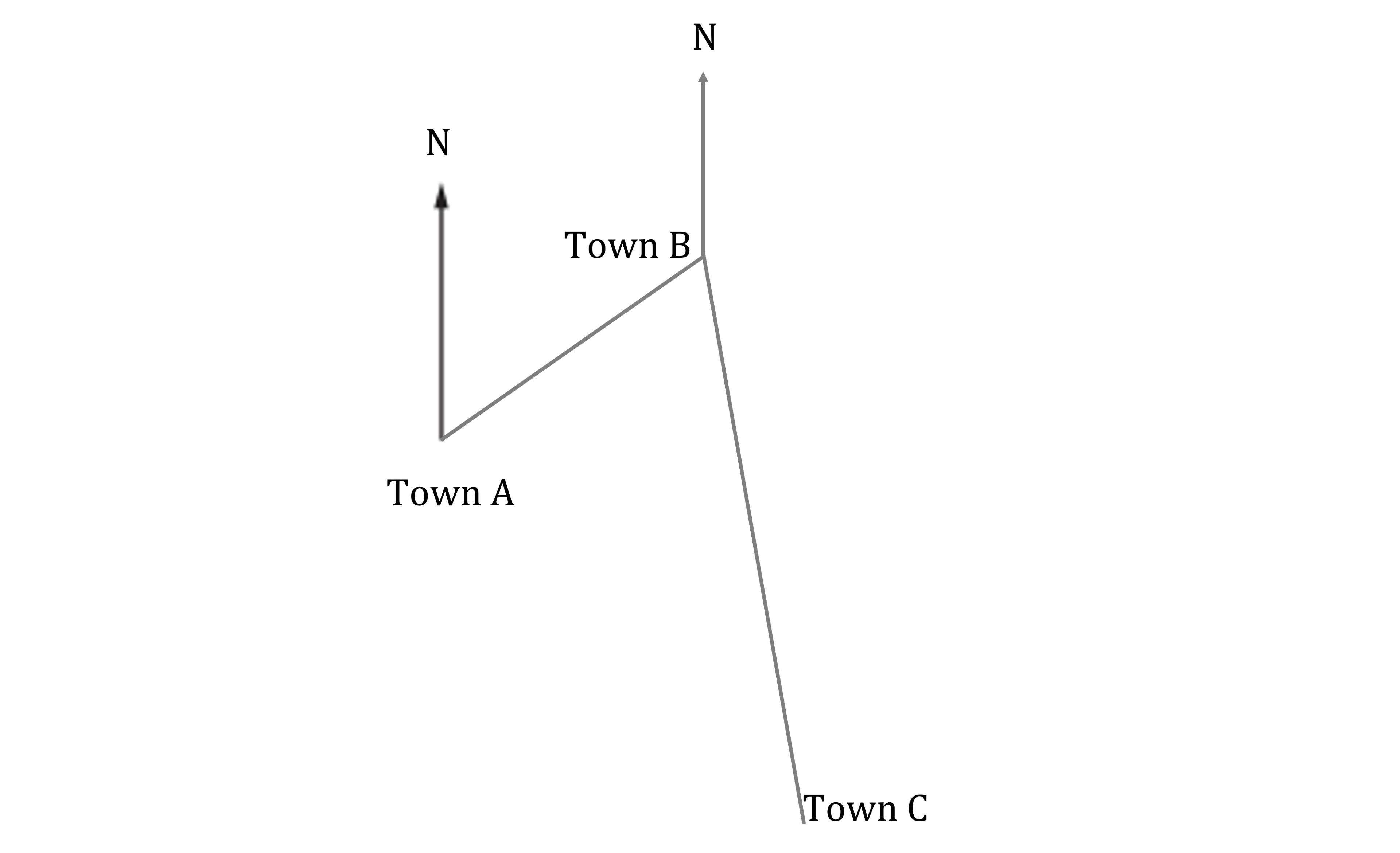
Diagram showing three towns connected by paths. Town A is southwest, Town B is northeast of A, and Town C is southeast of B. North is indicated.

(b)

Join Town C to Town A with a straight line

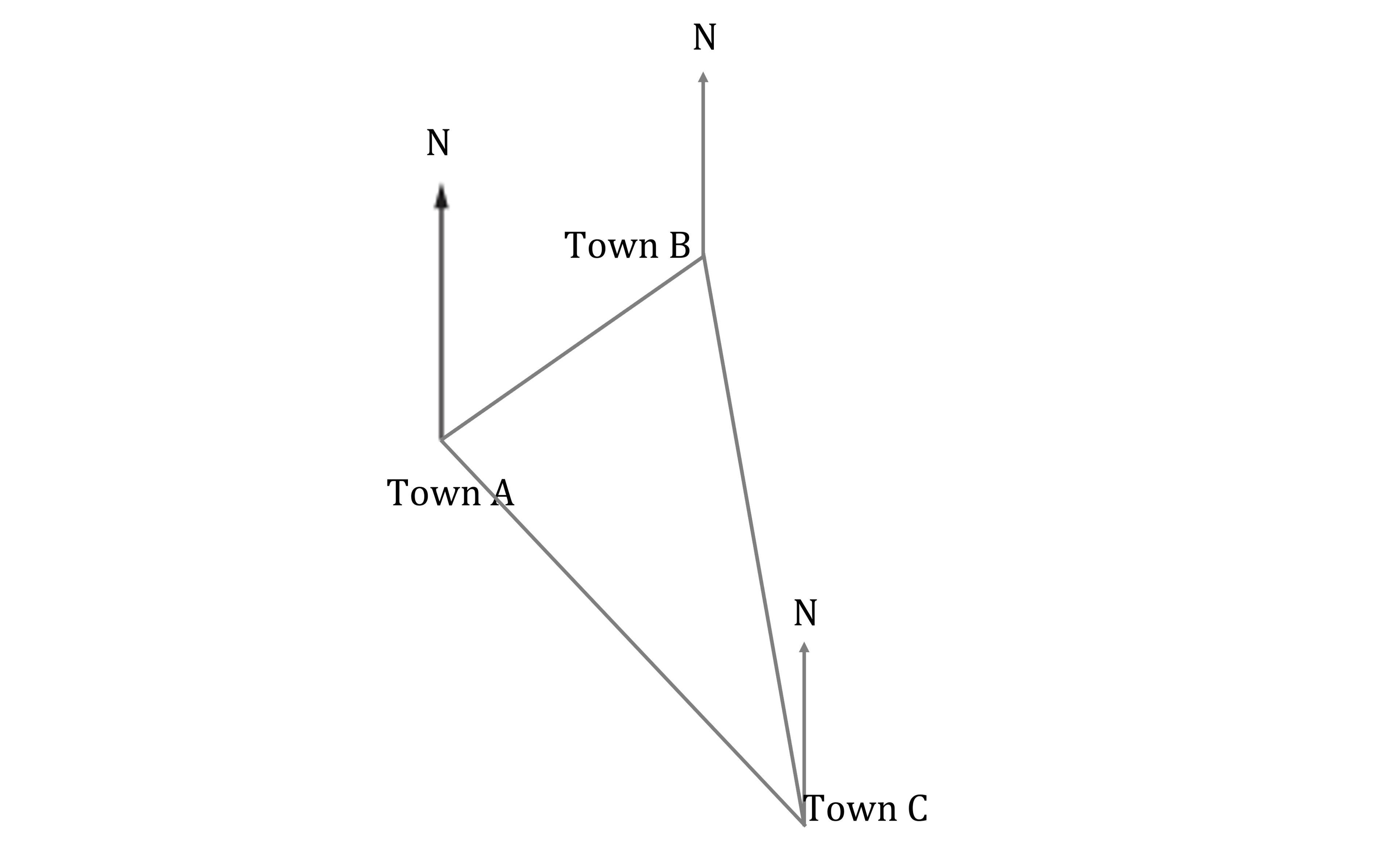
Map diagram showing towns A, B, and C connected with lines. Arrows point north from each town, with A to B to C forming a triangle.

Measure the line and multiply by 5 to find the actual distance

5.8 cross times 5 equals 29

Measure the bearing from Town C to Town A

29 km on bearing 317°

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:BearingsNext:Container Packing
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Roger B

    Reviewer: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.