Scale Drawings (SQA National 5 Applications of Mathematics): Revision Note
Exam code: X844 75
Scale drawings
What is a scale?
A scale refers to a ratio
This ratio describes the relationship between the drawn size and the real-life size
Maps are usually drawn to a scale
The ratio will work for any unit of length applied to both sides
The scale can be given without units
e.g. 1 : 10,000 means 1 cm on the drawing is 10,000 cm in real life
The scale can be given with different units
e.g. 1 cm : 100 m means 1 cm on the drawing is 100 m in real life
Examiner Tips and Tricks
When working with lots of different units and converting between them, make sure to use "common sense" checks. For example, when converting 500 km into metres, think whether you are expecting a bigger or smaller number.
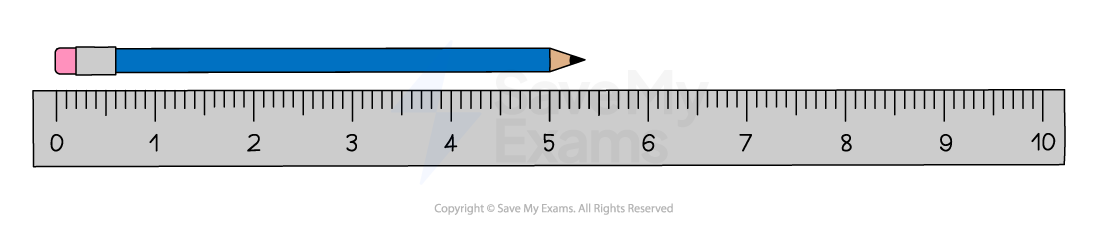
How do I measure or draw a line accurately?
You need to have a ruler which uses millimetres
Align 0 on the ruler with the starting point
Make sure the ruler is in the required direction
For measuring:
find where the endpoint meets the ruler
read off the number to the nearest millimetre
For drawing:
draw a straight line using the ruler from 0 to the required measurement
How can I use a scale to find lengths for an accurate drawing?
Questions normally ask you to draw a navigation course to scale
STEP 1
Divide the actual distance by the relevant part of the ratioe.g. suppose the scale is 1 cm : 1.5 km and the actual distance between A and B is 5.4 km
the scale distance is 5.4 ÷ 1.5 = 3.6 cm
STEP 2
Measure this distance from the starting pointe.g. measure 3.6 cm from A in the direction that will be given
How can I use a scale to find the actual lengths from a map?
Questions sometimes ask you to find the actual distance between two points using a map
STEP 1
Use a ruler to measure the distance accurately on the mape.g. measuring a length from A to B as 5.8 cm
STEP 2
Use the scale to find the actual distance in the same unitse.g. suppose the scale is 1 cm : 1500 m
the actual distance = 5.8 × 1500 m = 8700 m
Examiner Tips and Tricks
When measuring or drawing lines in the exam, you are given a tolerance of ±1 mm. This means that if a line is 4.6 cm, and you measure it as 4.7 cm, then you still get the mark. However, 4.8 cm would not get the mark.
Worked Example
Angus is on holiday in Llanfyllin, Wales. He wants to travel to Thetford, England.
Use the map and the scale 1 cm : 40 km to find the actual distance between Llanfyllin and Thetford.
Answer:
Use your ruler to measure the distance between the two towns on the map
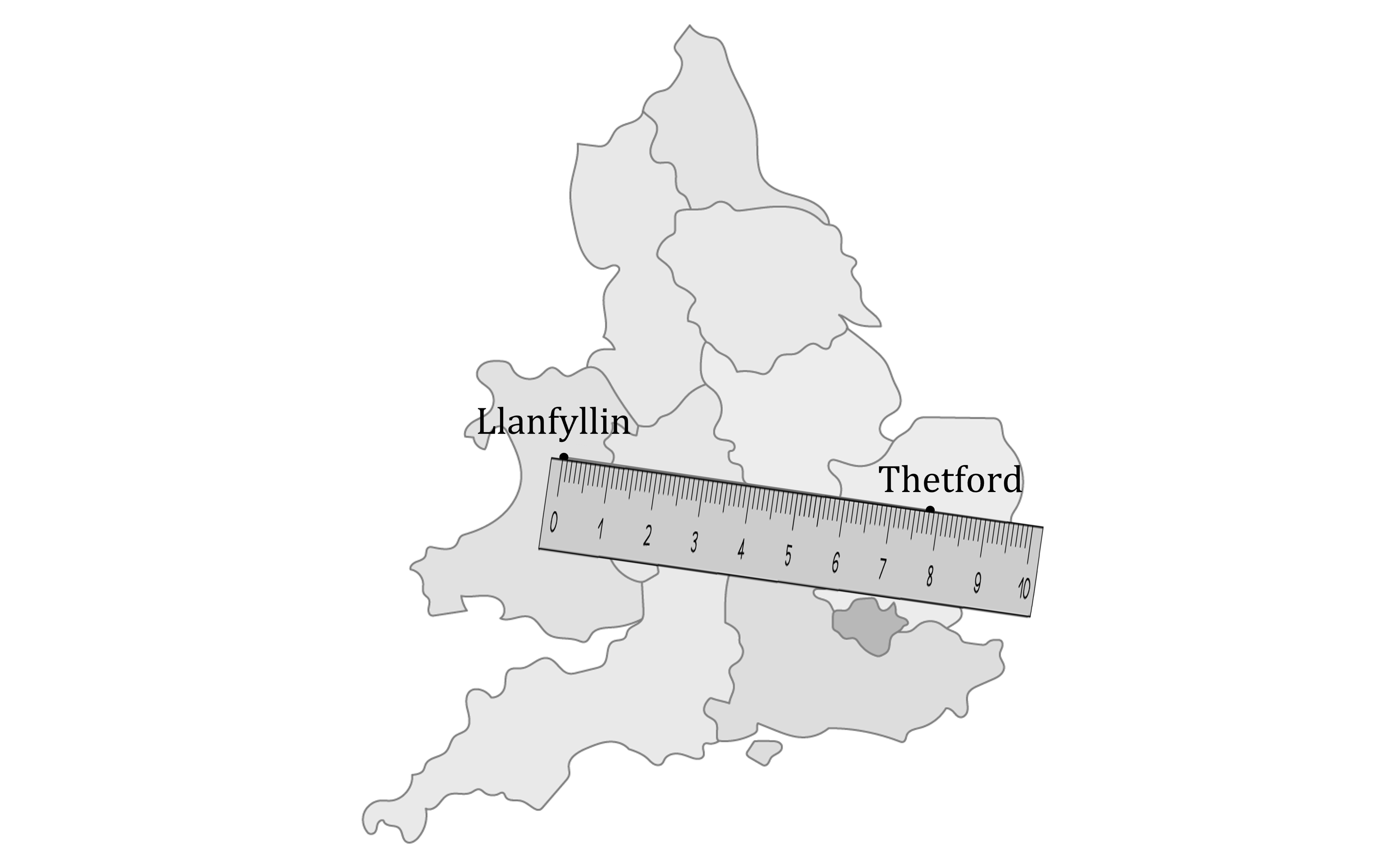
7.8 cm
Multiply the distance by the scale
7.8 × 40 = 312
312 km

Unlock more, it's free!
Was this revision note helpful?
