National 5PhysicsSQARevision NotesDynamicsVectors & ScalarsScale Diagrams

Scale Diagrams (SQA National 5 Physics): Revision Note

Exam code: X857 75

Katie M

Written by: Katie M

Reviewed by: Leander Oates

Updated on

Scale diagrams

Representing vectors

  • Vectors can be represented using arrows drawn to scale

    • The length of the arrow represents the magnitude of the vector

    • The direction of the arrow indicates the direction of the vector

    • The length of the arrows must be proportional to their magnitudes

Three horizontal arrows labeled "v" (5 m/s EAST), "2v" (10 m/s EAST), and "3v" (15 m/s EAST), showing increasing speeds to the right.
The lengths of vector arrows are proportional to their magnitudes. The 10 m/s vector arrow is twice as long as the 5 m/s vector arrow, and the 15 m/s vector arrow is three times as long as the 5 m/s arrow

Constructing scale diagrams

  • A scale diagram can be used to find the resultant of two vectors, such as displacement, velocity, or force, using the following steps:

    • Step 1: Choose an appropriate scale

      • e.g. 1 cm = 100 m, 1 cm = 1 m s-1 , or 1 cm = 5 N

    • Step 2: Draw the vectors head-to-tail

    • Step 3: Draw the resultant vector from the start (the tail) of the first arrow to the end (the arrow head) of the second

    • Step 4: Measure the length of the resultant vector using a ruler and convert it using your chosen scale

    • Step 5: Measure the angle with a protractor

      • If using compass bearings, measure the angle from due North

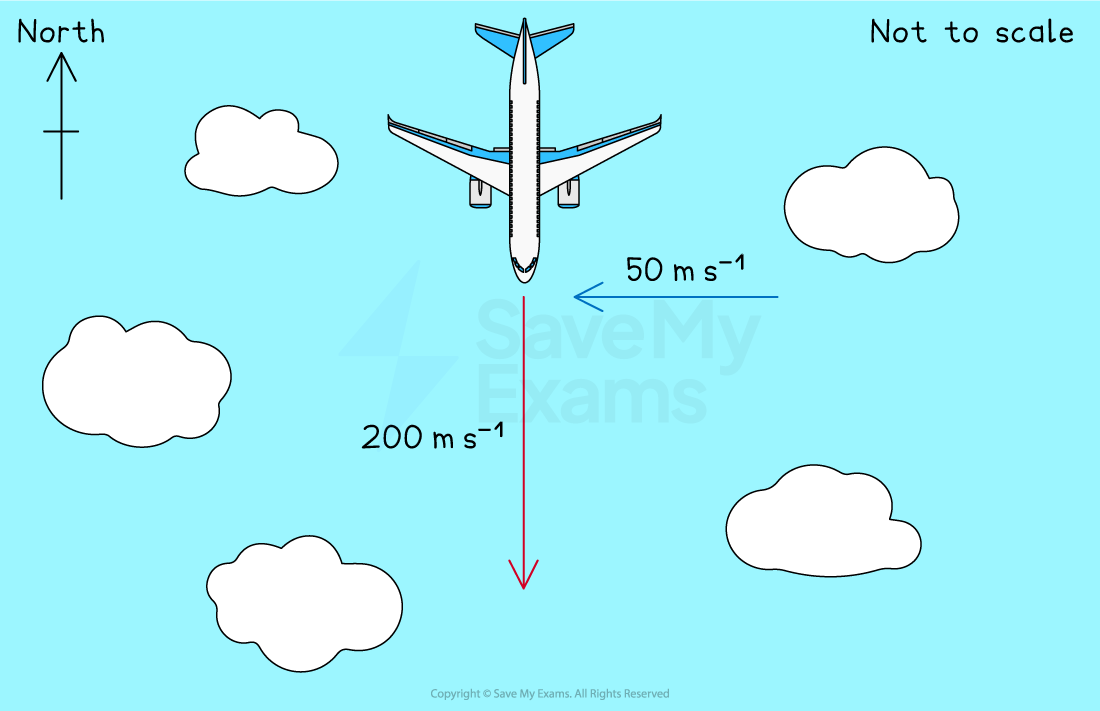
  • If an aeroplane is travelling due south at 200 m s-1 and the wind is moving due west at 50 m s-1, then using a scale of 1 cm = 25 m s-1:

    • The velocity of the aeroplane would be 8 cm long

    • The velocity of the wind would be 2 cm long

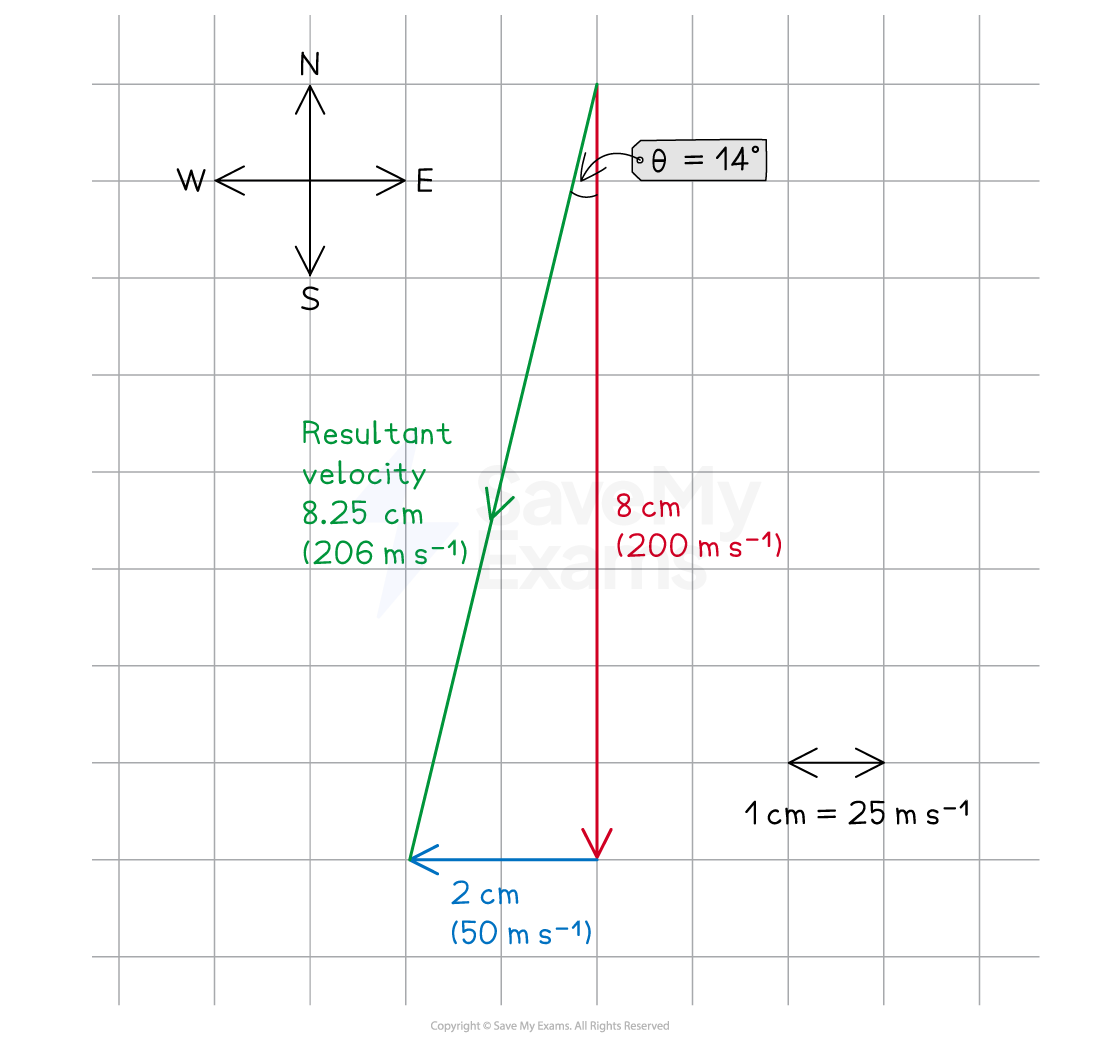
  • The size of the resultant velocity would be about 8.25 cm long, which is equivalent to 8.25 × 25 = 206 m s-1

  • The direction of the resultant velocity would be about 14° E of S or a bearing of (14 + 180 =) 194

Using a scale diagram to find resultant velocity

Aeroplane flying south at 200 m/s with wind speed of 50 m/s from east. Sky background with scattered clouds. Compass indicates north. Not to scale.
Vector diagram showing velocities: 2 cm (50 m/s) east, 8 cm (200 m/s) north, resulting in 8.25 cm (206 m/s) at 14° northeast; scale 1 cm = 25 m/s.
A scale diagram must include the chosen scale, the vector arrows drawn head-to-tail, and the resultant vector clearly labelled with measurements

Worked Example

A hiker walks from point A to point F following the route shown.

Route map showing points A to F with distances: A-B 1 km south, B-C 8 km east, C-D 14 km north, D-E 2 km west, E-F 3 km south. North arrow and "not to scale" noted.

By scale diagram or otherwise, determine the resultant displacement of the hiker from point A to point F.

Answer:

Step 1: Calculate the total displacement in each direction

  • The total displacement in the north direction is

14 space plus space open parentheses negative 3 close parentheses space plus open parentheses negative 1 close parentheses space equals space 10 space km

  • The total displacement in the east direction is

8 space plus space open parentheses negative 2 close parentheses space equals space 6 space km

Step 2: Choose a sensible scale

  • For the two vectors, 6 km and 10 km, a scale of 1 cm = 1 km would be appropriate

Step 3: Draw the two components using a ruler and make the measurements accurate to 1 mm

2-4-resolving-vectors-1st-we-step-2_edexcel-al-physics-rn

Step 4: Draw the resultant vector, remembering the start and finish points of the journey

2-4-resolving-vectors-1st-we-step-3_edexcel-al-physics-rn

Step 5: Carefully measure the length of the resultant and convert using the scale

2-4-resolving-vectors-1st-we-step-4_edexcel-al-physics-rn

Step 6: Measure the angle between the vector and the horizontal line

2-4-resolving-vectors-1st-we-step-5_edexcel-al-physics-rn

Step 7: Write the complete answer, giving both magnitude and direction

  • Magnitude of the resultant displacement = 11.7 km

  • Direction of the resultant displacement (as a bearing) = 031

  • For direction, you could also say 59° N of E or 31° E of N

Examiner Tips and Tricks

In exam questions, the vectors will always be along the same line or at right angles to each other. When producing a scale diagram, you must use a sharp pencil, ruler and protractor to ensure all the lengths and angles are as accurate as possible. If you are confident performing calculations with vectors, then it is a good idea to use these methods (i.e. Pythagoras' theorem and trigonometry) to double-check your answer.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Calculations with VectorsNext:Motion Relationships
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Leander Oates

    Reviewer: Leander Oates

    Expertise: Physics Content Creator

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.