A LevelFurther MathsEdexcelFurther Pure 1Revision NotesCoordinate SystemsProperties of Ellipses, Parabolas & HyperbolasProperties of Hyperbolas

Properties of Hyperbolas (Edexcel A Level Further Maths): Revision Note

Exam code: 9FM0

Mark Curtis

Last updated

Properties of hyperbolas

What is a hyperbola?

  • A hyperbola is a curve with the Cartesian equation

    • x squared over a squared minus y squared over b squared equals 1

    • which consists of two separate branches

      • the positive-x branch (x greater or equal than a)

      • the negative-x branch (x less or equal than negative a)

    • that are bounded by the two asymptotes

      • y equals plus-or-minus b over a x

    • which pass through the origin

      • and are not necessarily perpendicular

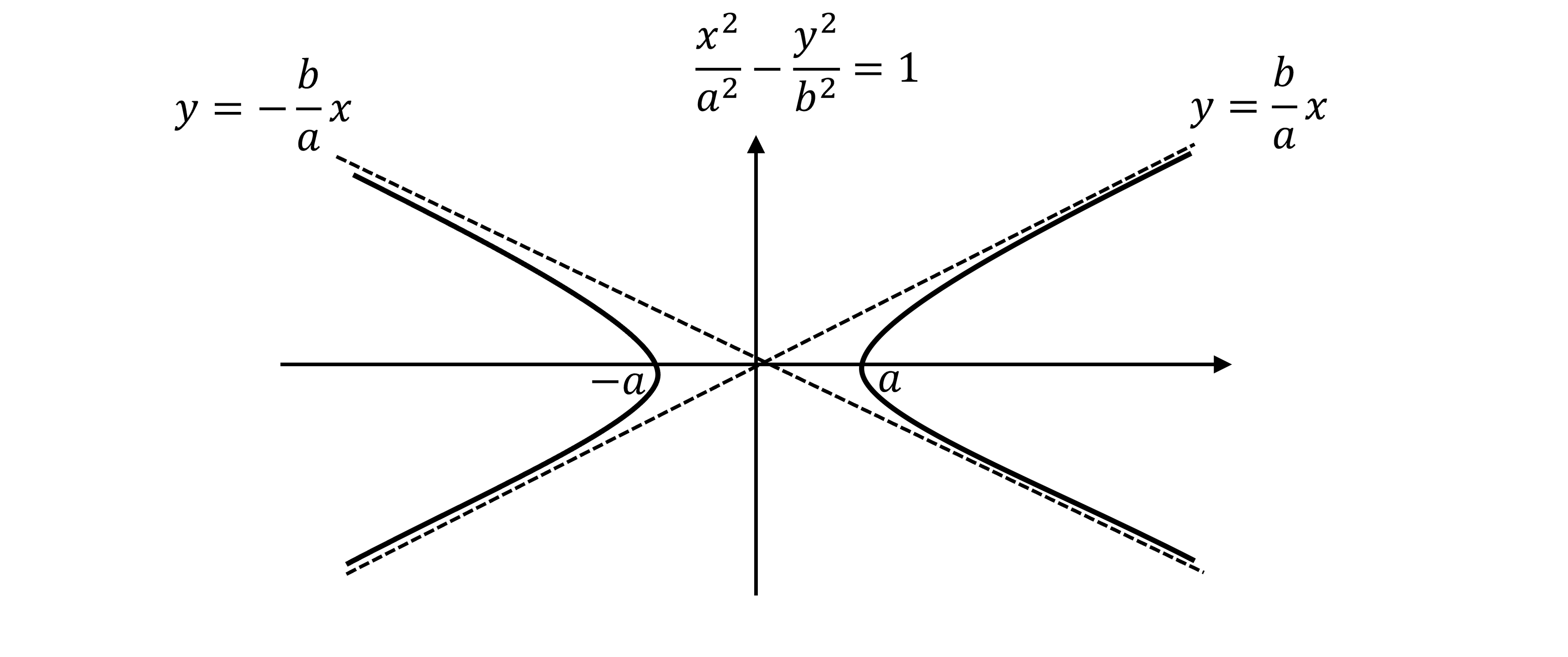
Graph of a hyperbola with asymptotes y = (±b/a)x. Equation x²/a² - y²/b² = 1. Axes labelled with −a and a intercepts. The hyperbola is the shape of two branches (a C shape on the right and a backwards C shape on the left).

  • The asymptote equations can be derived by rearranging the curve

    • y squared equals fraction numerator b squared x squared over denominator a squared end fraction open parentheses 1 minus a squared over x squared close parentheses so y equals plus-or-minus square root of fraction numerator b squared x squared over denominator a squared end fraction end root square root of 1 minus a squared over x squared end root

      • as x rightwards arrow infinity, a squared over x squared rightwards arrow 0 so second square root tends to 1 and y rightwards arrow plus-or-minus b over a x

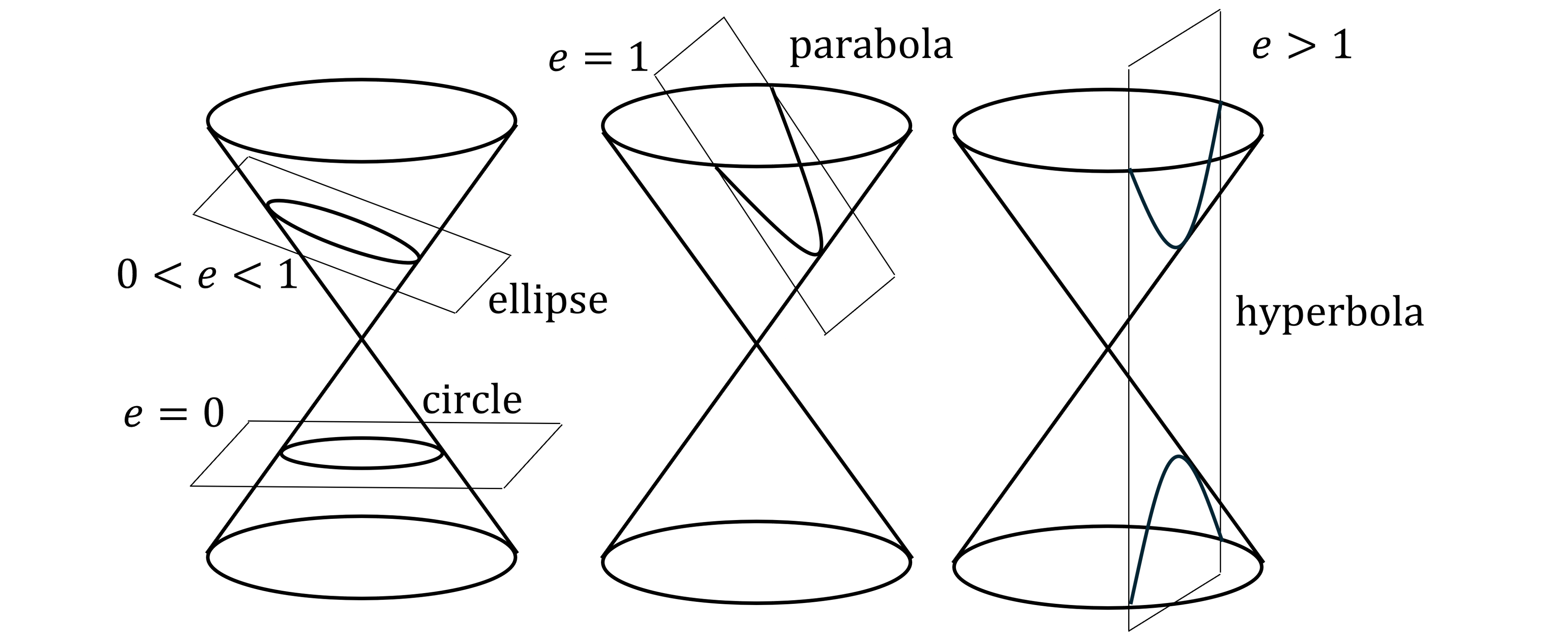
  • A hyperbola is one of the conic curves

    • with eccentricity e greater than 1

Diagram of conic sections showing circles, ellipses, parabolas, and hyperbolas formed by intersecting a plane with cones.

Examiner Tips and Tricks

You are given the Cartesian equation of a hyperbola and the equations of the asymptotes in the formulae booklet.

What are the parametric equations of a hyperbola?

  • There are two different sets of parametric equations for a hyperbola that are both equally valid

  • The first set of parametric equations is

    • x equals plus-or-minus a cosh theta

    • y equals b sinh theta

    • where theta element of straight real numbers

      • and plus-or-minus depends on positive or negative-x branch

  • The second set of parametric equations is

    • x equals a sec theta

    • y equals b tan theta

    • where negative pi over 2 less than theta less than pi over 2 defines the positive-x branch

      • as sec theta is positive

    • and both negative pi less than theta less than negative pi over 2 and pi over 2 less than theta less or equal than pi define the negative-x branch

      • as sec theta is negative

    • and theta not equal to plus-or-minus pi over 2

      • as sec theta and tan theta are undefined

  • Eliminating the parameter, theta, gives the Cartesian equation x squared over a squared minus y squared over b squared equals 1

    • using either cosh squared theta minus sinh squared theta identical to 1

    • or 1 plus tan squared theta identical to sec squared theta and rearranging

Examiner Tips and Tricks

You are given both sets of parametric equations of a hyperbola in the formulae booklet (but not the ranges of theta).

Examiner Tips and Tricks

In the exam, unless given (or seen in subsequent results), you can use either set of parametric equations for a hyperbola.

What are the coordinates of a general point on a hyperbola?

  • A general point P on the hyperbola x squared over a squared minus y squared over b squared equals 1 has coordinates given by its parametric equations, P open parentheses a cosh theta comma space b sinh theta close parentheses or P open parentheses a sec theta comma space b tan theta close parentheses

Graph of a hyperbola with asymptotes, labelled with equations. Point P has either coordinates (a cosh theta, b sinh theta) or (a sec theta, b tan theta)

  • e.g. P open parentheses 3 sec theta comma space 2 tan theta close parentheses is a general point on the hyperbola x squared over 9 minus y squared over 4 equals 1

    • It satisfies the equation of the curve

    • It moves around the curve depending on the value of theta

  • This is different to, say, open parentheses 3 comma space 0 close parentheses

    • which is a fixed point on the hyperbola x squared over 9 minus y squared over 4 equals 1

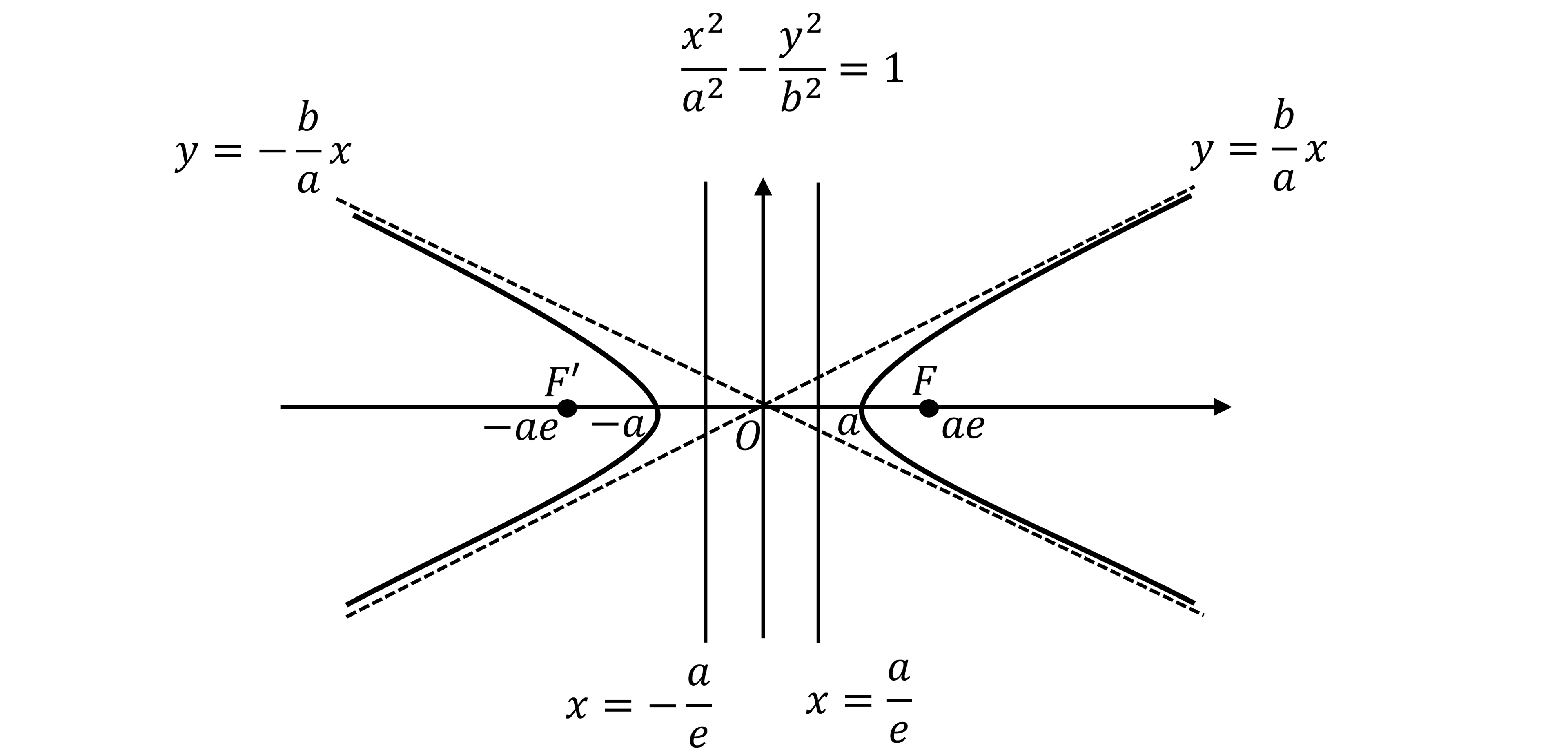
What is the eccentricity, focus and directrix of a hyperbola?

  • The eccentricity of a hyperbola, e, takes the range e greater than 1

  • If a greater than b

    • the eccentricity is found be rearranging the following formula

      • b squared equals a squared open parentheses e squared minus 1 close parentheses

    • the foci, F and F apostrophe, are two symmetric points on the x-axis enclosed by either branch

      • with coordinates open parentheses plus-or-minus a e comma space 0 close parentheses

    • the directrices are the two vertical lines positioned symmetrically either side of the origin

      • in the gap between the branches

      • with equations x equals plus-or-minus a over e

Diagram showing a hyperbola x^2/a^2-y^2/b^2=1 with asymptotes y=(b/a)x and y=-(b/a)x, labelled axes, and focal points F and F' at ae and -ae on the x-axis. Two vertical lines x=-a/e and x=a/e are shown (directrices).

Examiner Tips and Tricks

You are given the eccentricity formula, foci and directrices of a hyperbola in the formulae booklet.

Worked Example

A hyperbola has the equation x squared over 16 minus y squared over 9 equals 1.

Calculate

(a) the coordinates of the foci,

(b) the equations of the directrices,

(c) the equations of any asymptotes.

Answer:

(a)

Find a and b by comparing to the general equation x squared over a squared minus y squared over b squared equals 1

a equals 4 b equals 3

Check that a greater than b

4 greater than 3

Rearrange the relationship b squared equals a squared open parentheses e squared minus 1 close parentheses to find e

  • and check that e greater than 1

table row cell 3 squared end cell equals cell 4 squared open parentheses e squared minus 1 close parentheses end cell row cell 9 over 16 end cell equals cell e squared minus 1 end cell row cell e squared end cell equals cell 9 over 16 plus 1 end cell row cell e squared end cell equals cell 25 over 16 end cell row e equals cell 5 over 4 end cell end table

Calculate the foci using open parentheses plus-or-minus a e comma space 0 close parentheses

open parentheses plus-or-minus 4 cross times 5 over 4 comma space 0 close parentheses

The foci have coordinates open parentheses plus-or-minus 5 comma space 0 close parentheses

(b)

Calculate the equations of the directrices using x equals plus-or-minus a over e

x equals plus-or-minus fraction numerator 4 over denominator open parentheses 5 over 4 close parentheses end fraction

The directrices have equations x equals plus-or-minus 16 over 5

(c)

Substitute a equals 4 and b equals 3 into y equals plus-or-minus b over a x

The asymptotes have equations y equals plus-or-minus 3 over 4 x

What is the focus-directrix property of a hyperbola?

  • The focus-directrix property says that, if you take any point P on a hyperbola, then

    • the distance from P to the focus, F

    • divided by the shortest distance from P to the directrix (at point D)

    • is always equal to e, the eccentricity

    • i.e. fraction numerator P F over denominator P D end fraction equals e

      • sometimes rearranged to P F equals e P D

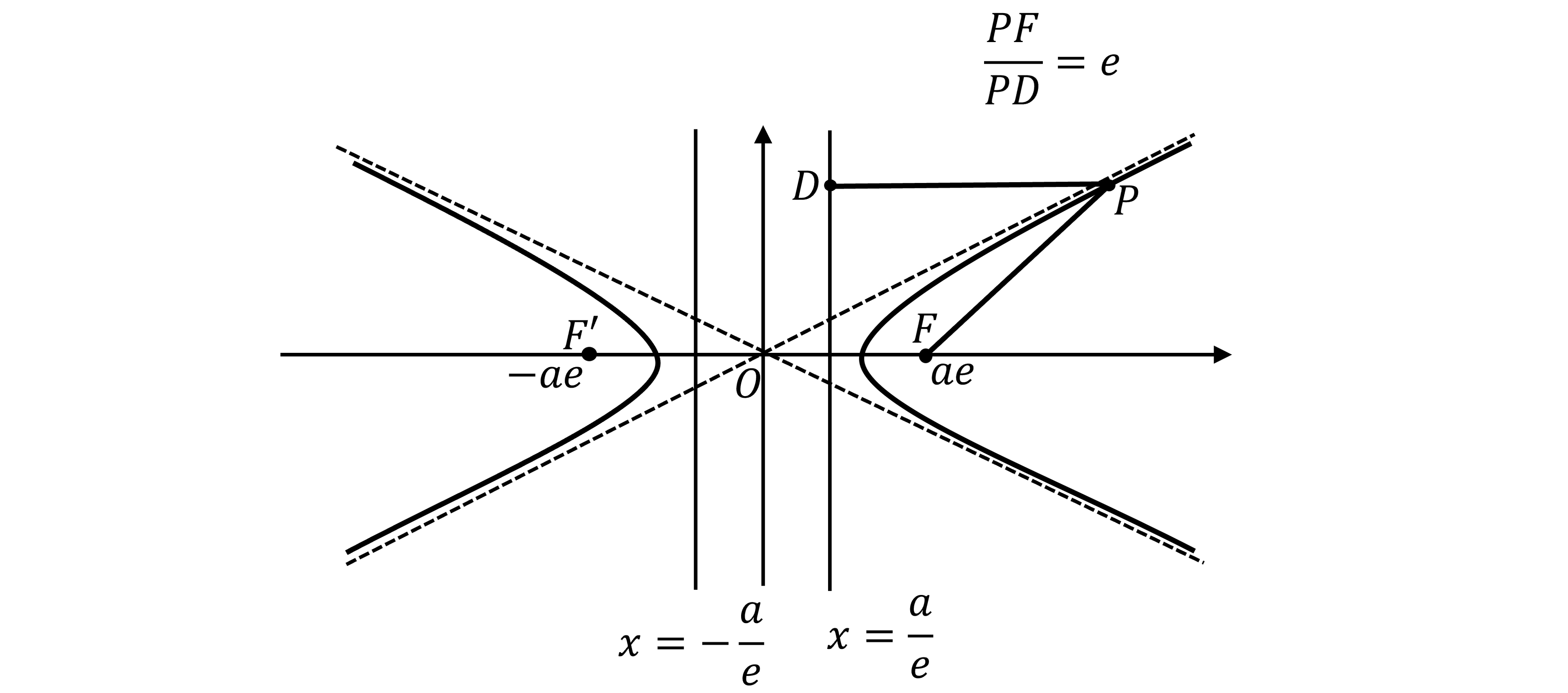
Diagram of a hyperbola with foci at F and F' at ae and -ae on the x-axis. A point P on the curve in the first quadrant is shown. The point D on the directrix x=a/e is shown at the same vertical height as P. Lines PD and PF are drawn. Formula for PF/PD = e.

  • The focus-directrix property works from P to the other focus, F apostrophe, and directrix, D apostrophe

    • fraction numerator P F apostrophe over denominator P D apostrophe end fraction equals e

      • where e is the same eccentricity

Examiner Tips and Tricks

You are not given the focus-directrix property in the exam (you must learn it).

Worked Example

One branch of a hyperbola with focus F at open parentheses a e comma space 0 close parenthesesand directrix x equals a over e is shown below.

The point P on the hyperbola has coordinates open parentheses x comma space y close parentheses and the point D is on the directrix, at the same height as P.

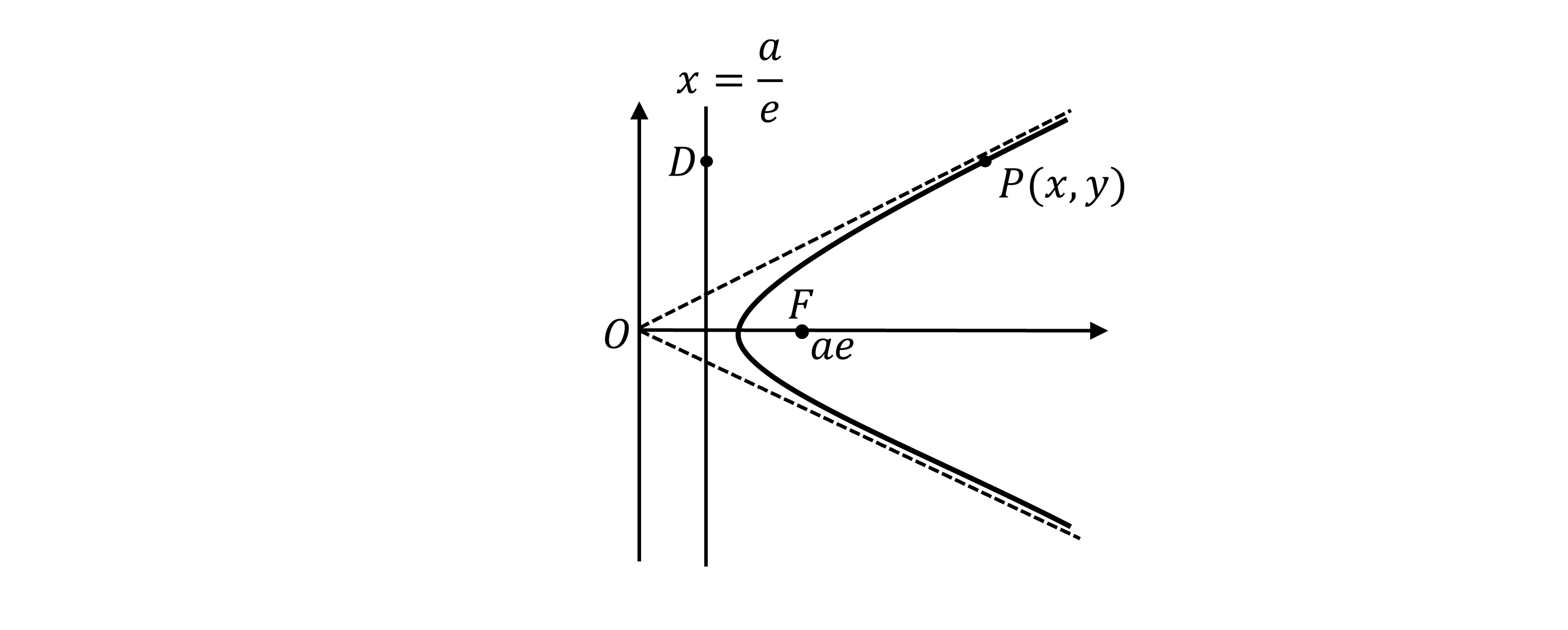
Diagram showing the right-hand branch of a hyperbola with the focus F at (ae, 0) and the directrix at x=a/e. A point P(x,y) is labelled on the curve.

Using only the focus-directrix property, derive the Cartesian equation of a hyperbola, x squared over a squared minus y squared over b squared equals 1, where b squared equals a squared open parentheses e squared minus 1 close parentheses

Answer:

Use the focus-directrix property on P, F and D (draw the lines P F and P D)

fraction numerator P F over denominator P D end fraction equals e

It helps to draw the lengths x and y from P open parentheses x comma space y close parentheses on the diagram

Create a right-angled triangle whose hypotenuse is P F with base open parentheses x minus a e close parentheses and height y

Diagram showing the right-hand branch of a hyperbola with the focus F at (ae, 0) and the directrix at x=a/e. A point P(x,y) is labelled on the curve. PF is a right-angled triangle with base (x-ae) and height y. The distance between x and the directrix is (x-a/e). The formula PF/PD=e is shown.

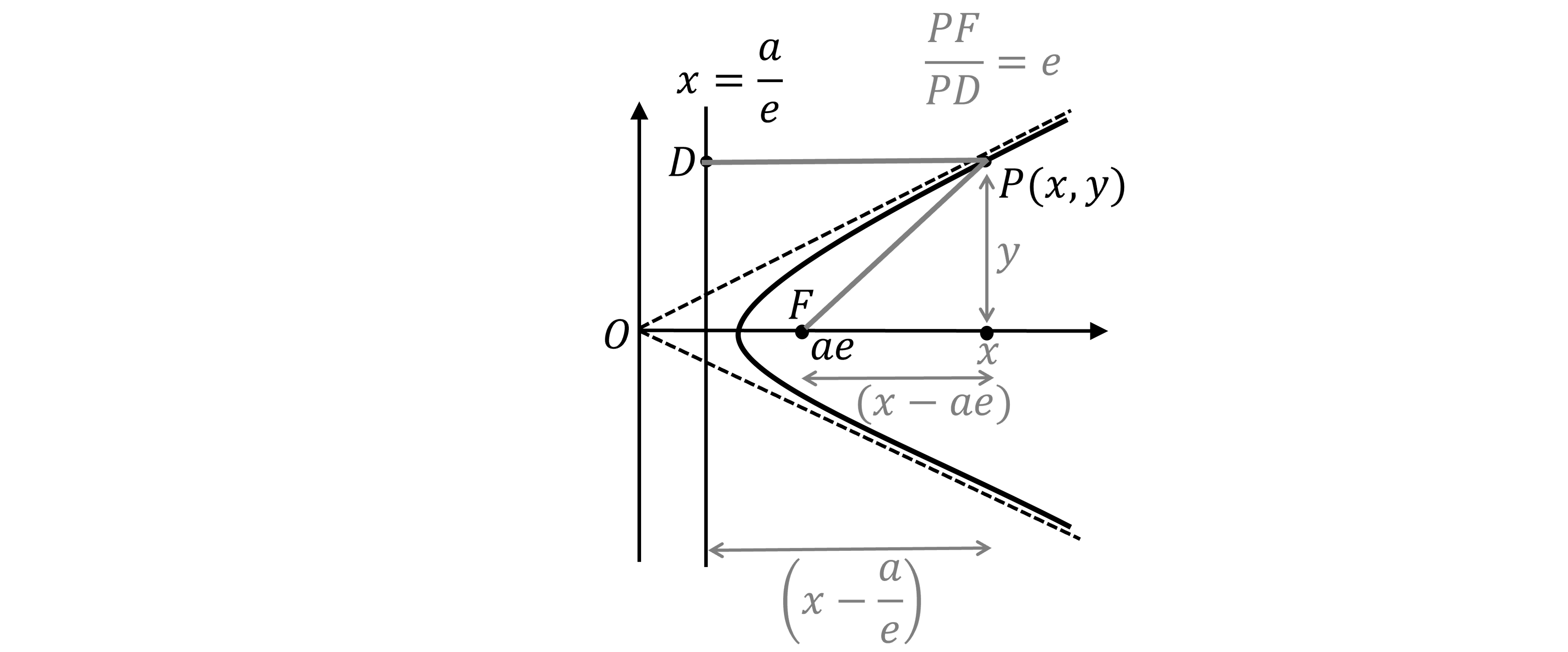
Use Pythagoras' theorem to find P F squared

P F squared equals open parentheses x minus a e close parentheses squared plus y squared

Find the length P D from x to the directrix

P D equals open parentheses x minus a over e close parentheses

Rearrange fraction numerator P F over denominator P D end fraction equals e to make P F squared the subject

P F squared equals e squared P D squared

Substitute in expressions for P F squared and P D squared from above

open parentheses x minus a e close parentheses squared plus y squared equals e squared open parentheses x minus a over e close parentheses squared

Expand, cancel and factorise

table row cell x squared minus 2 a e x plus a squared e squared plus y squared end cell equals cell e squared open parentheses x squared minus fraction numerator 2 a x over denominator e end fraction plus a squared over e squared close parentheses end cell row cell x squared up diagonal strike negative 2 a e x end strike plus a squared e squared plus y squared end cell equals cell e squared x squared up diagonal strike negative 2 a e x end strike plus a squared end cell row cell a squared open parentheses e squared minus 1 close parentheses end cell equals cell open parentheses e squared minus 1 close parentheses x squared minus y squared end cell end table

Divide both sides by a squared open parentheses e squared minus 1 close parentheses

1 equals x squared over a squared minus fraction numerator y squared over denominator a squared open parentheses e squared minus 1 close parentheses end fraction

This now has the correct form of a hyperbola

The Cartesian equation is x squared over a squared minus y squared over b squared equals 1, where b squared equals a squared open parentheses e squared minus 1 close parentheses

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent

Our rating represented in Trustpilot stars
Read more reviews
Previous:Properties of ParabolasNext:Properties of Rectangular Hyperbolas
Mark Curtis

Author: Mark Curtis

Expertise: Maths Content Creator

Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.