Tangents & Normals to Parabolas (Edexcel A Level Further Maths): Revision Note

Exam code: 9FM0

Author

Mark Curtis

Last updated

7 January 2026

Tangents & normals to parabolas

What is a tangent or a normal to a parabola at a general point?

The position of the general point $P (a t^{2}, 2 a t)$ on the parabola $y^{2} = 4 a x$ depends on $t$
It is possible to calculate equations of tangents and normals at $P (a t^{2}, 2 a t)$
- where the coefficients are in terms of $t$
  - i.e. as $P$ varies, the equations vary

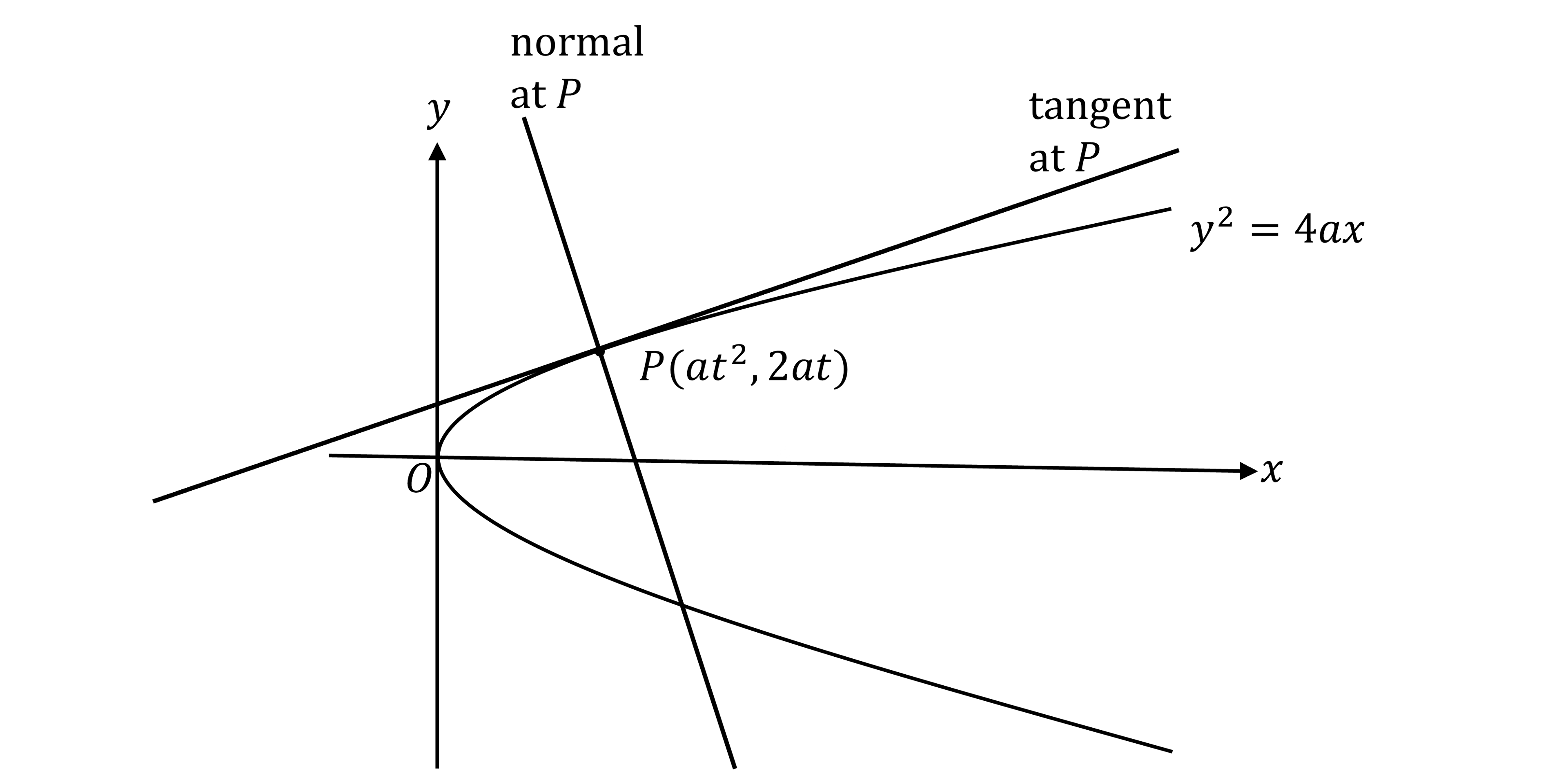
Graph of a parabola y^2 = 4ax with axes, showing point P(at^2, 2at), tangent and normal lines at P.

In general
- at the point $P (a t^{2}, 2 a t)$ on the parabola $y^{2} = 4 a x$
  - $- x + t y = a t^{2}$ is the tangent
  - $t x + y = 2 a t + a t^{3}$ is the normal
Be careful with the infinite gradient at the vertex
- The equation of the tangent at $(0, 0)$ is $x = 0$

Examiner Tips and Tricks

You are not expected to remember the general formulae for tangents and normals, but you are expected to be able to work them out using the steps below.

How do I find the equation of a tangent to a parabola?

To find the equation of the tangent to the parabola $y^{2} = 4 a x$ at the general point $P (a t^{2}, 2 a t)$ :
STEP 1
Find the gradient $m_{T}$ of the tangent at $P (a t^{2}, 2 a t)$ in terms of $t$
- either by implicit differentiation of $y^{2} = 4 a x$ to find $\frac{d y}{d x}$
  - then substituting $x = a t^{2}$ and $y = 2 a t$ into the result
- or by parametric differentiation of $x = a t^{2}$ and $y = 2 a t$
  - using $\frac{d y}{d x} = \frac{d y}{d t} \times \frac{d t}{d x} = \frac{(\frac{d y}{d t})}{(\frac{d x}{d t})}$
STEP 2
Substitute into the equation of a straight line $y - y_{1} = m_{T} (x - x_{1})$ the following:
- $m_{T}$ in terms of $t$
- $x_{1} = a t^{2}$
- $y_{1} = 2 a t$
- and simplify

Examiner Tips and Tricks

It is possible to make $y$ the subject of $y^{2} = 4 a x$ to find $\frac{d y}{d x}$ , i.e. $y = \pm \sqrt{4 a x}$ , but differentiating this is more messy than implicit or parametric differentiation!

Worked Example

Show that the tangent to the parabola $y^{2} = 8 x$ at the point $P (2 t^{2}, 4 t)$ has the equation

$- x + t y = 2 t^{2}$

Answer:

The tangent has the equation $y - y_{1} = m_{T} (x - x_{1})$

Method 1

Use implicit differentiation to differentiate $y^{2} = 8 x$

$2 y \frac{d y}{d x} = 8$

Substitute $y = 4 t$ into the result and rearrange for $\frac{d y}{d x}$

$\begin{array}{rcl} 2 (4 t) \frac{d y}{d x} & = & 8 \\ 8 t \frac{d y}{d x} & = & 8 \\ \frac{d y}{d x} & = & \frac{1}{t} \end{array}$

Method 2

Use parametric differentiation to find $\frac{d y}{d x}$ from $x = 2 t^{2}$ and $y = 4 t$

$\begin{array}{rcl} \frac{d y}{d x} & = & \frac{d y}{dt} \times \frac{d t}{d x} \\ \frac{d y}{d x} & = & \frac{(\frac{d y}{d t})}{(\frac{d x}{d t})} \\ \frac{d y}{d x} & = & \frac{4}{4 t} \\ \frac{d y}{d x} & = & \frac{1}{t} \end{array}$

After either method, substitute $m_{T} = \frac{1}{t}$ , $x_{1} = 2 t^{2}$ and $y_{1} = 4 t$ into $y - y_{1} = m_{T} (x - x_{1})$

$y - 4 t = \frac{1}{t} (x - 2 t^{2})$

Rearrange into the form given in the question

$\begin{array}{rcl} t y - 4 t^{2} & = & x - 2 t^{2} \\ - x + t y & = & - 2 t^{2} + 4 t^{2} \end{array}$

Collect like terms to get the final answer

$- x + t y = 2 t^{2}$

What is the tangent condition for a parabola?

The condition for a straight line $y = m x + c$ to be a tangent to the parabola $y^{2} = 4 a x$ is that the gradient $m$ and y-intercept $c$ of the straight line must satisfy
- $a = m c$
You need to know how to prove this condition
- by solving $y = m x + c$ and $y^{2} = 4 a x$ simultaneously
- and forcing the discriminant to be zero
  - See the worked example below

Worked Example

Prove that, if $y = m x + c$ is tangent to $y^{2} = 4 a x$ , then $a m = c$ .

Answer:

First substitute $y = m x + c$ into the equation $y^{2} = 4 a x$

${(m x + c)}^{2} = 4 a x$

Expand and rearrange into a three-term quadratic in $x$

$\begin{array}{rcl} m^{2} x^{2} + 2 m c x + c^{2} & = & 4 a x \\ m^{2} x^{2} + (2 m c - 4 a) x + c^{2} & = & 0 \end{array}$

The solutions to this equation are the $x$ -intercepts of the points of intersection

Force the discriminant to be zero, as a tangent only touches the parabola once

${(2 m c - 4 a)}^{2} - 4 m^{2} c^{2} = 0$

Expand and simplify

$\begin{array}{rcl} 4 m^{2} c^{2} - 16 m c a + 16 a^{2} - 4 m^{2} c^{2} & = & 0 \\ 16 a^{2} & = & 16 m c a \end{array}$

Divide both sides by $a$ l (as $a > 0$ in $y^{2} = 4 a x$ ) to get the correct answer

$a = m c$

How do I find the equation of a normal to a parabola?

To find the equation of the normal to the parabola $y^{2} = 4 a x$ at the general point $P (a t^{2}, 2 a t)$ :
- follow the previous steps for finding the equation of a tangent
  - but use $y - y_{1} = m_{N} (x - x_{1})$ as the equation of the normal
  - where $m_{N} = - \frac{1}{m_{T}}$ is the negative reciprocal of the tangent gradient

Worked Example

Show that the normal to the parabola $y^{2} = 4 a x$ at the point $P (a t^{2}, 2 a t)$ has the equation

$t x + y = 2 a t + a t^{3}$

Answer:

The normal has the equation $y - y_{1} = m_{N} (x - x_{1})$ where the normal gradient is the negative reciprocal of the tangent gradient, $m_{N} = - \frac{1}{m_{T}}$

Method 1

Use implicit differentiation to differentiate $y^{2} = 4 a x$

$2 y \frac{d y}{d x} = 4 a$

Substitute $y = 2 a t$ into the result and rearrange for $\frac{d y}{d x}$ (the gradient of the tangent)

$\begin{array}{rcl} 2 (2 a t) \frac{d y}{d x} & = & 4 a \\ 4 a t \frac{d y}{d x} & = & 4 a \\ \frac{d y}{d x} & = & \frac{1}{t} \end{array}$

Method 2

Use parametric differentiation to find $\frac{d y}{d x}$ (the gradient of the tangent) from $x = a t^{2}$ and $y = 2 a t$

$\begin{array}{rcl} \frac{d y}{d x} & = & \frac{d y}{d t} \times \frac{d t}{d x} \\ \frac{d y}{d x} & = & \frac{(\frac{d y}{d t})}{(\frac{d x}{d t})} \\ \frac{d y}{d x} & = & \frac{2 a}{2 a t} \\ \frac{d y}{d x} & = & \frac{1}{t} \end{array}$

After either method, convert the tangent gradient into the normal gradient (e.g. find the negative reciprocal, or use $m_{N} = - \frac{1}{m_{T}}$ )

$m_{N} = - t$

Substitute $m_{N} = - t$ , $x_{1} = a t^{2}$ and $y_{1} = 2 a t$ into $y - y_{1} = m_{N} (x - x_{1})$

$y - 2 a t = - t (x - a t^{2})$

Rearrange into the form given in the question

$\begin{array}{rcl} y - 2 a t & = & - t x + a t^{3} \\ t x + y - 2 a t & = & a t^{3} \end{array}$

Add $2 a t$ to both sides

$t x + y = 2 a t + a t^{3}$

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent

Tangents & Normals to Parabolas (Edexcel A Level Further Maths): Revision Note

Tangents & normals to parabolas

What is a tangent or a normal to a parabola at a general point?

How do I find the equation of a tangent to a parabola?

What is the tangent condition for a parabola?

How do I find the equation of a normal to a parabola?

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Further Trigonometry

The t-formulae

Trig identities using t-formulae

Trig Equations using t-formulae

Modelling using t-formulae

Further Calculus

Taylor Series

Taylor Series

Limits using Series

Series Solutions to Differential Equations

Methods in Calculus

Leibnitz's Theorem

L'Hospital's Rule

The Weierstrass Substitution

Further Differential Equations

Reducing Differential Equations

Reducing First-Order Differential Equations

Reducing Second-Order Differential Equations

Coordinate Systems

Properties of Ellipses, Parabolas & Hyperbolas

Properties of Ellipses

Properties of Parabolas

Properties of Hyperbolas

Properties of Rectangular Hyperbolas

Tangent & Normals to Ellipses, Parabolas & Hyperbolas

Tangents & Normals to Ellipses

Tangents & Normals to Parabolas

Tangents & Normals to Hyperbolas

Tangents & Normals to Rectangular Hyperbolas

Loci Problems

Loci Problems

Further Vectors

Further Vectors

Vector (Cross) Product

Scalar Triple Product

Vector Geometry with Points, Lines & Planes

Shortest Distances using Vector Rules

Areas & Volumes using Vector Rules

Direction Ratios & Direction Cosines

Further Numerical Methods

Further Numerical Methods

Numerical Solutions of First-Order Differential Equations

Numerical Solutions of Second-Order Differential Equations

Simpson's Rule

Inequalities

Inequalities

Solving Inequalities involving Algebraic Fractions

Solving Inequalities involving Modulus Functions

Author: Mark Curtis