Explain what is meant by the ultimate tensile strength of a material.
A footbridge is supported by a number of metal cables of the same length.
Each cable has uniform cross-section and diameter 4.20 mm as shown in Fig. 16.1.

Fig. 16.1 (not to scale)
A group of engineers investigate how the extension x varies with applied force F for one of the cables.
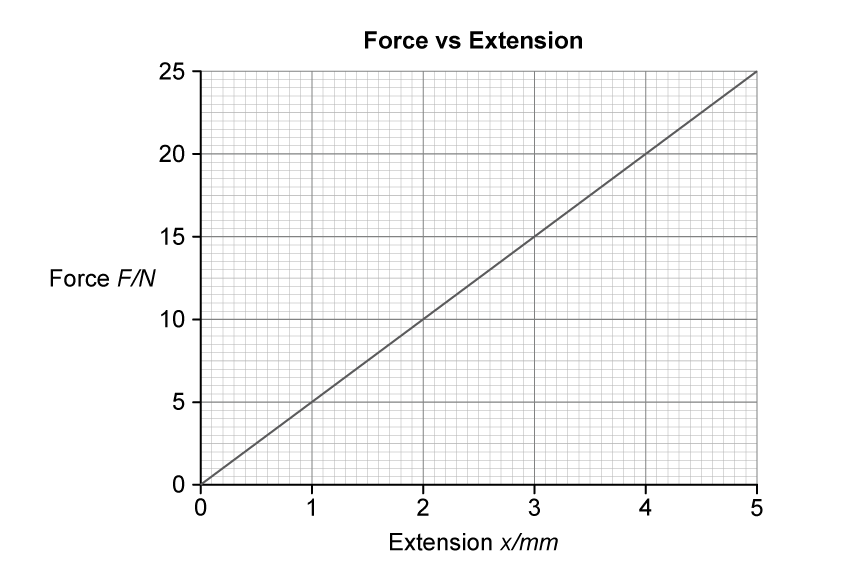
The results of the investigation are shown in Fig. 16.2.

Fig. 16.2
The cable breaks when the force is 2.2 kN.
i) Describe how a suitable measuring device may have been used by the engineers to demonstrate that the cable had uniform cross-section.
[2]
ii) State any value of F when the cable behaves
elastically
F = ............................................ kN
plastically.
F = ............................................ kN
[2]
iii) Use Fig. 16.2 to determine the force constant k in Nm–1 of the cable.
k = ............................................... Nm–1 [2]
Determine the breaking stress σ of the cable.
Assume that the cross-sectional area of the cable remains constant during the test.
σ = .................................... Pa [2]
Explain why the work done on the cable when its extension changes from 3.0 mm to 4.0 mm is greater than when its extension changes from 1.0 mm to 2.0 mm.
Was this exam question helpful?