Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)HLRevision Notes2. FunctionsFunctions ToolkitSelf-Inverse Functions

Self-Inverse Functions (DP IB Analysis & Approaches (AA)): Revision Note

Dan Finlay

Written by: Dan Finlay

Reviewed by: Mark Curtis

Updated on

DP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): HL

Self-inverse functions

What are self-inverse functions?

  • A function f left parenthesis x right parenthesis is called self-inverse if it is equal to its inverse function f to the power of negative 1 end exponent left parenthesis x right parenthesis

    • f left parenthesis x right parenthesis equals space f to the power of negative 1 end exponent left parenthesis x right parenthesis

  • Applying f to both sides of f left parenthesis x right parenthesis equals space f to the power of negative 1 end exponent left parenthesis x right parenthesis gives

    • left parenthesis f ring operator f right parenthesis left parenthesis x right parenthesis equals f f open parentheses x close parentheses equals x

      • as f of f to the power of negative 1 end exponent cancels out on the right-hand side

Examiner Tips and Tricks

Knowing that a self inverse function satisfies both f left parenthesis x right parenthesis equals space f to the power of negative 1 end exponent left parenthesis x right parenthesis and f f open parentheses x close parentheses equals x can help in harder algebraic questions.

What are examples of self-inverse functions?

  • Examples of common self-inverse functions include

    • the identity function space f left parenthesis x right parenthesis equals x

    • the reciprocal function space f left parenthesis x right parenthesis equals 1 over x

    • Linear functions with a gradient of -1

      • e.g. space f left parenthesis x right parenthesis equals 8 minus x

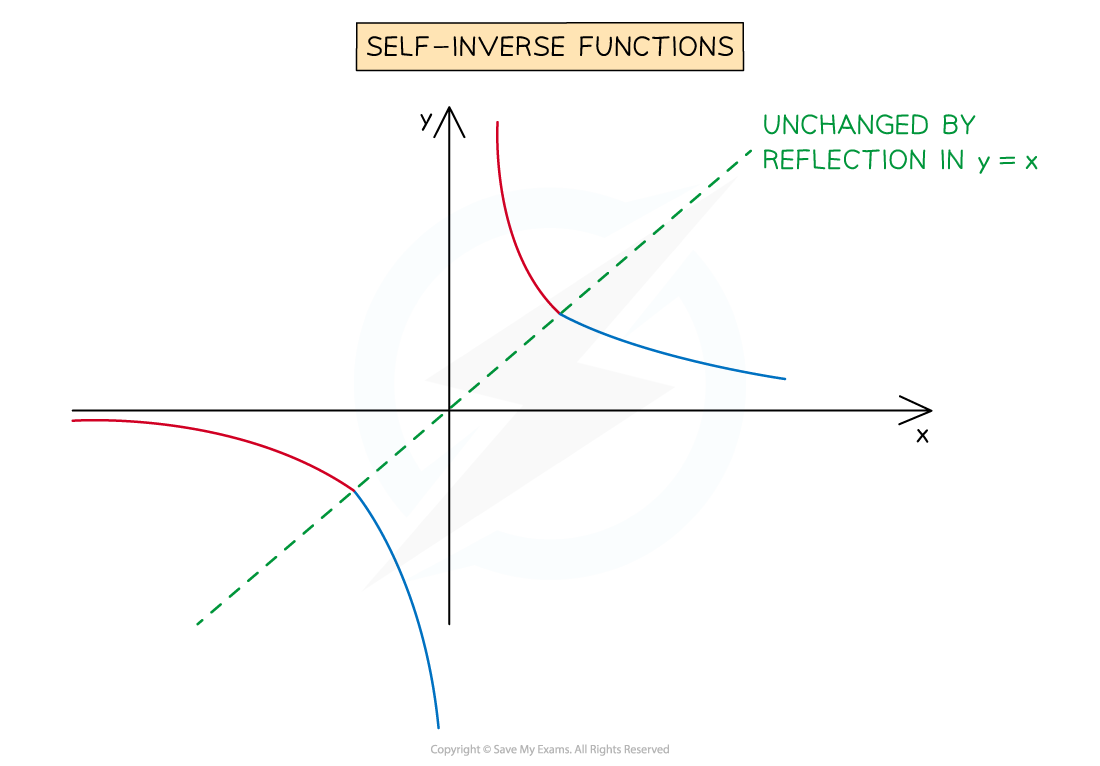
What do the graphs of self-inverse functions look like?

  • The graph of a self-inverse function has reflective symmetry

    • The graph is unchanged by a reflection in the line y equals x

Graph of self-inverse functions showing a red and blue curve reflected over a green dashed line y = x, with reflective symmetry about the line y = x.

Examiner Tips and Tricks

If you are using algebra to prove that f left parenthesis x right parenthesis is self-inverse and get a different expression for f to the power of negative 1 end exponent left parenthesis x right parenthesis , try plotting both graphs on your GDC.

  • If they both overlap, then your f to the power of negative 1 end exponent left parenthesis x right parenthesis can be rearranged to give f left parenthesis x right parenthesis

  • If they do not overlap, there's a mistake in your working!

Worked Example

Use algebra to show that the function space f open parentheses x close parentheses equals fraction numerator 7 x minus 5 over denominator x minus 7 end fraction comma blank x not equal to 7 is self-inverse.

2-3-3-ib-aa-hl-self-inverse-functions-we-solution

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Periodic FunctionsNext:Graphing Functions & Their Key Features
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Mark Curtis

    Reviewer: Mark Curtis

    Expertise: Maths Content Creator

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.