Prime Factor Decomposition (AQA GCSE Maths): Revision Note
Exam code: 8300
Did this video help you?
Prime factor decomposition
What are prime factors?
A factor of a given number is a value that divides the given number exactly, with no remainder
e.g. 6 is a factor of 18
A prime number is a number which has exactly two factors; itself and 1
e.g. 5 is a prime number, as its only factors are 5 and 1
You should remember the first few prime numbers:
2, 3, 5, 7, 11, 13, 17, 19, …
The prime factors of a number are therefore all the primes which multiply to give that number
e.g. The prime factors of 30 are 2, 3, and 5
2 × 3 × 5 = 30
How do I find prime factors?
Use a factor tree to find prime factors
Split the number up into a pair of factors
Then split each of those factors up into another pair
Continue splitting up factors along each "branch" until you get to a prime number
These can not be split into anything other than 1 and themselves
It helps to circle the prime numbers at the end of the branches
One way to split each number up is by dividing it by the smallest possible prime number
This gives a prime factor at each stage

Another way to split each number up by dividing by easy numbers such as 10
These do not need to be prime numbers
You will need to split any non-prime numbers into pairs of factors
These trees can get messy

The number will always end up with the same numbers circled no matter which pairs of numbers you choose
A number can be uniquely written as a product of prime factors
Write the prime factors as a multiplication, in ascending order
360 = 2 × 2 × 2 × 3 × 3 × 5
This can then be written more concisely using powers
360 = 23 × 32 × 5
Examiner Tips and Tricks
Exam questions on this topic will ask you to express a number as a product of its prime factors. You should simplify your final answer by using indices. You need to show your working clearly to gain full marks.
Worked Example
Express 432 as the product of its prime factors. Show your working clearly.
Answer:
Create a factor tree
Start with 432 and choose any two numbers that multiply together to make 432
2 and 216 is an obvious pair
Continue to split non-prime numbers into pairs of factors
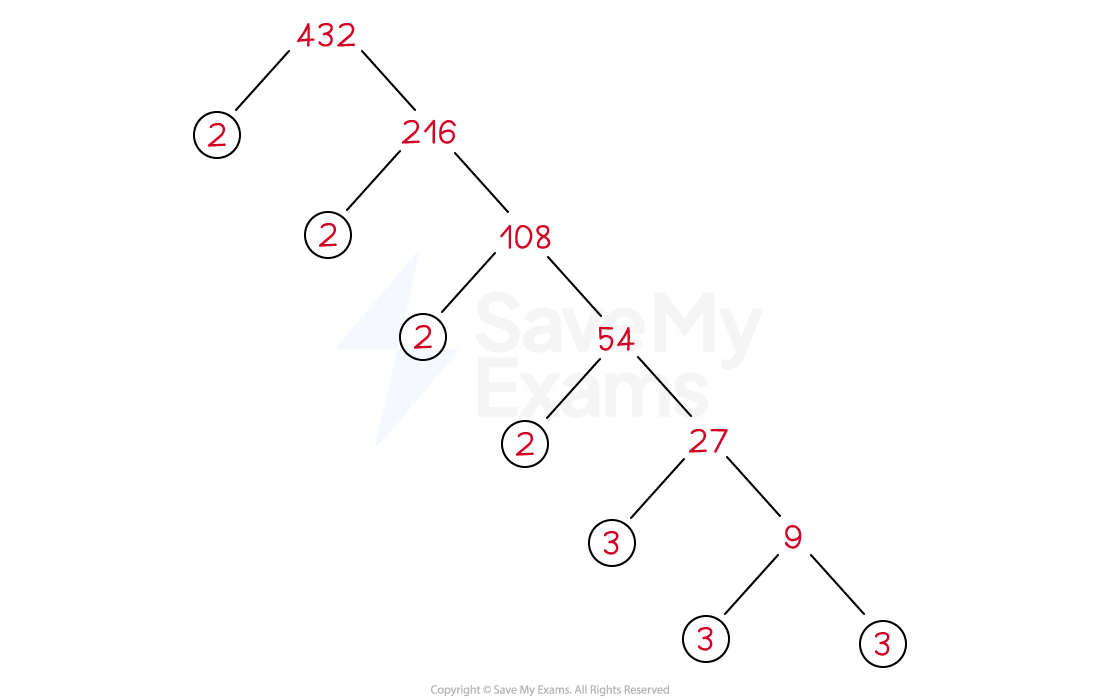
The answer will be the same regardless of the factors chosen in the first step
Write the prime numbers out as a product
Any repeated prime factors can be written as a power

Unlock more, it's free!
Was this revision note helpful?
