Converting to & from Standard Form (WJEC Eduqas GCSE Maths): Revision Note

Converting to and from standard form

What is standard form and why is it used?

• Standard form is a way of writing numbers using powers of 10

• It is helpful to see the size of very large and very small numbers

• This allows us to:

  • Write them more concisely

  • Compare them more easily

  • Perform calculations with them more easily

How do I write a number in standard form?

• Numbers written in standard form are always written as:

• Where:

  • ( is bigger than or equal to 1 and less than 10)

  • is an integer

    • ( is negative) for numbers bigger than 0 and less than 1

    • for numbers bigger than or equal to 1 and less than 10

    • ( is positive) for numbers bigger than or equal to 10

How do I write a large number in standard form?

• To write a large number such as 32 400 in standard form

  • Identify the value of

    • 3.24

  • Find how many times you must multiply 3.24 by 10, to make 32 400

    • Count how many places you need to move the digits

    • We need to multiply by 10 four times

  • 32 400 = 3.24 × 10 × 10 × 10 × 10 = 3.24 × 10⁴

How do I write a small number in standard form?

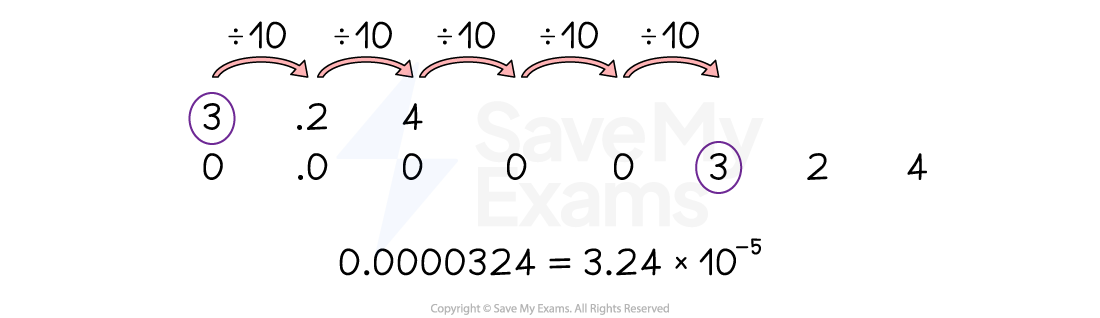
• To write a small number such as 0.0000324 in standard form

  • Identify the value of

    • 3.24

  • Find how many times you must divide 3.24 by 10, to make 0.0000324

    • Count how many places you need to move the digits

    • We need to divide by 10 five times

    • We are dividing rather than multiplying so the power will be negative

  • 0.0000324 = 3.24 ÷ 10 ÷ 10 ÷ 10 ÷ 10 ÷ 10 = 3.24 × 10^-5