Geometric Proof with Vectors (Edexcel IGCSE Further Pure Maths): Revision Note

Exam code: 4PM1

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on 20 October 2024

Vector Paths

How do I use vector paths?

A vector path is a path of vectors taking you from a start point to an end point
On the diagram shown
- F to B has the path F to A to B
  - $\vec{F B} = \vec{F A} + \vec{A B}$
- There are other possible paths too
  - F to G to B
You can write vector paths in terms of vectors given (a, b, ...)
- The rule $\vec{X Y} = - \vec{Y X}$ helps
  - $\vec{F B} = \vec{F A} + \vec{A B} = - \vec{A F} + \vec{A B} = - b + a$
Vectors given can be used to build bigger paths
- $\vec{F M} = \vec{F G} + \vec{G H} + \vec{H M} = a + a + b = 2 a + b$
  - Different correct paths simplify to the same final answer

How do I use ratios in vector paths?

Convert ratios into fractions
In the example shown, if $A X : X B = 3 : 5$ then
- $\vec{A X} = \frac{3}{8} \vec{A B}$
- $\vec{X B} = \frac{5}{8} \vec{A B}$
  - The ratio 3:5 has 3 + 5 = 8 parts
Always check which ratio you are being asked for
- $\vec{A X} = \frac{3}{5} \vec{X B}$
- $\vec{X B} = \frac{5}{3} \vec{A X}$

Examiner Tips and Tricks

Mark schemes will accept different correct paths, as long as the final answer is fully simplified.
Check for symmetries in the diagram to see if the vectors given can be used anywhere else.

Worked Example

The following diagram shows a grid formed of identical parallelograms.

Vectors $a$ and $b$ are given by $\vec{A B}$ and $\vec{A F}$ respectively.

Find the following vectors in terms of $a$ and $b$ , fully simplifying your answer.

(a) $\vec{E K}$

There are many ways to get from E to K
One option is E to O (b twice) then O to K ( -a four times).

$\begin{array}{rcl} \vec{E K} & = & \vec{E J} + \vec{J O} + \vec{O N} + \vec{N M} + \vec{M L} + \vec{L K} \\ = & b + b - a - a - a - a \end{array}$

$\vec{E K} = 2 b - 4 a$

-4a + 2b also accepted

(b) $\vec{A X}$ , where $X$ is the point on the line $A T$ such that $A X : X T = 1 : 3$ .

Start by imagining the vector $\begin{array}{rcl} \vec{A T} \end{array}$
It is easy to write this vector in terms of a and b

$\begin{array}{rcl} \vec{A T} \end{array} = 4 a + 3 b$

To find $\begin{array}{rcl} \vec{A X} \end{array}$ , use the given ratio to write it as a fraction of $\begin{array}{rcl} \vec{A T} \end{array}$
There are 1 + 3 = 4 parts

$\begin{array}{rcl} \vec{A X} & = & \frac{1}{4} \vec{A T} \end{array}$

Substitute in the known expression for $\begin{array}{rcl} \vec{A T} \end{array}$
Expand and simplify to get the final answer

$\begin{array}{rcl} \vec{A X} & = & \frac{1}{4} (4 a + 3 b) \\ = & a + \frac{3}{4} b \end{array}$

$\begin{array}{rcl} \vec{A X} & = & a + \frac{3}{4} b \end{array}$

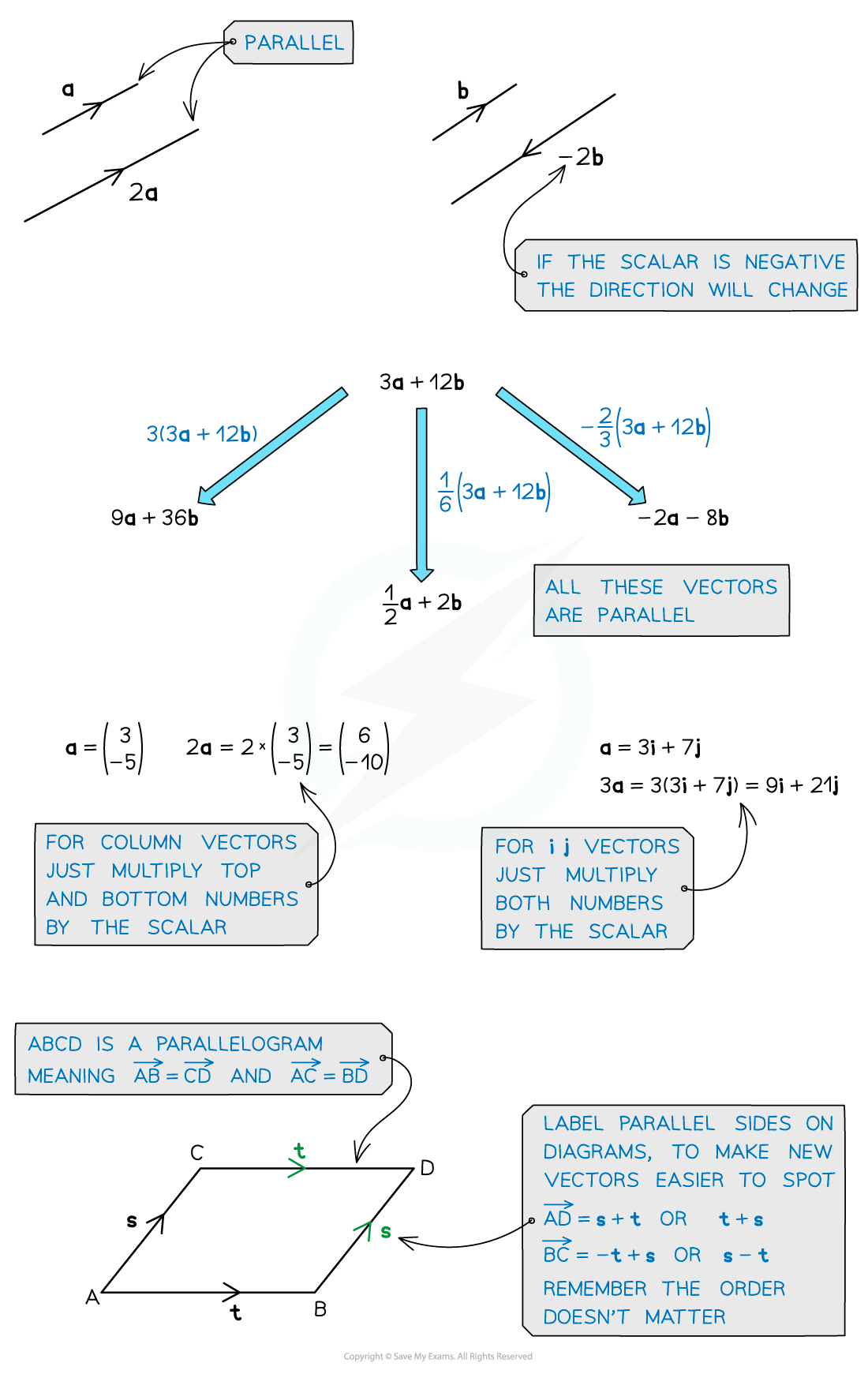
Parallel Vectors

How do I know if two vectors are parallel?

Two vectors are parallel if one is a scalar multiple of the other
- This means if b is parallel to a, then b = ka
  - where k is a constant number (scalar)
For example, $a = (\begin{matrix} 1 \\ 3 \end{matrix})$ and $b = (\begin{matrix} 2 \\ 6 \end{matrix})$
- $(\begin{matrix} 2 \\ 6 \end{matrix}) = 2 \times (\begin{matrix} 1 \\ 3 \end{matrix})$ so $b = 2 a$
- b is a scalar multiple of a, so b is parallel to a
If the scalar multiple is negative, then the vectors are parallel and in opposite directions
- $c = (\begin{matrix} - 3 \\ - 9 \end{matrix}) = - 3 a$
  - c is parallel to a and in the opposite direction

How do I use factorisation to show two vectors are parallel?

If two vectors factorise with a common bracket, then they are parallel
- They can be written as scalar multiples
For example
- 9a + 6b factorises to 3(3a + 2b)
- 12a + 8b factorises to 4(3a + 2b)
- This means $12 a + 8 b = \frac{4}{3} (9 a + 6 b)$
  - so they are scalar multiples of each other
  - and therefore parallel

Examiner Tips and Tricks

If a question asks you to show that two vectors are parallel
- Don't stop after showing two vectors are scalar multiples of each other
- You must conclude with "therefore a and b are parallel" to get all the marks!

Worked Example

Show that the vectors $a = 2 p - 4 q$ and $b = 6 q - 3 p$ are parallel.

It helps to write b in the same order as a

$b = - 3 p + 6 q$

Factorise both vectors to form a common bracket

$\begin{array}{rcl} a & = & 2 (p - 2 q) \\ b & = & - 3 (p - 2 q) \end{array}$

Write b in terms of a
It can help to make the brackets the subject of the first equation, i.e. $(p - 2 q) = \frac{a}{2}$
Then substitute that into the equation for b

$b = - 3 \times \frac{a}{2} = - \frac{3}{2} a$

Write a conclusion showing the scalar multiple
State that this shows they are parallel

$b = - \frac{3}{2} a$ therefore b is parallel to a

You could also use $a = - \frac{2}{3} b$

Collinearity

What does collinear mean?

The points A , B and C are collinear if they all lie along the same straight line
In the image on the left in the diagram below, the following vectors are all parallel:
- $\vec{A B}, \vec{B C}, \vec{A C}, \vec{B A}, \vec{C A}, \vec{C B}$

How do I use vectors to show that three points are collinear?

To show the points A , B and C are collinear
- prove that two line segments are parallel
- and show that there is at least one point that lies on both segments
  - This makes them parallel and connected (not side-by-side)
For example, if you show that $\vec{B C} = 2 \vec{A B}$ then
- the line segments AB and BC are parallel
- and they have a common point, B
  - So A , B and C must be collinear
Similarly, $\vec{A C} = 3 \vec{A B}$ means AC and AB are parallel
- and they have a common point, A
  - so A , B and C must be collinear

How can collinearity be used when extend lines?

Extending the line segment OA means continuing the straight line beyond A
- If the extended line passes through the point X
  - then O , A and X are collinear
To test whether another point, Y , is on OA extended
- test whether O , A and Y are collinear

Examiner Tips and Tricks

Even though it's 'obvious' that $\vec{A B}$ and $\vec{A C}$ have a common point at A, you should still write this fact in your answer to complete a collinearity proof.

Worked Example

The diagram shows a quadrilateral, $O A B C$ , where

$\vec{O A} = 2 a$

$\vec{O C} = c$

It is also know that

$\vec{O B} = 2 a + 3 c$

(a) Juan believe that the point $X$ , which is halfway along $A C$ , lies on the line $O B$ .

Show that $O$ , $X$ and $B$ are not collinear.

O , X and B are collinear if two line segments are parallel and share a common point
Consider the vectors $\vec{O X}$ and $\vec{O B}$
They have a common point, O
Check if they are parallel by first finding $\vec{O X}$

$\begin{array}{rcl} \vec{O X} & = & \vec{O A} + \frac{1}{2} \vec{A C} \\ = & 2 a + \frac{1}{2} (\vec{A O} + \vec{O C}) \\ = & 2 a + \frac{1}{2} (- 2 a + c) \end{array}$

Expand and simplify

$\begin{array}{rcl} \vec{O X} & = & 2 a - a + \frac{1}{2} c \\ = & a + \frac{1}{2} c \end{array}$

Now compare it to $\vec{O B} = 2 a + 3 c$ (given in the question)
Try factorisation to write $\vec{O B}$ in terms of $\vec{O X}$

$\begin{array}{rcl} \vec{O B} & = & 2 a + 3 c \\ = & 2 (a + \frac{3}{2} c) \end{array}$

The $a$ inside the brackets matches the $a$ in $\vec{O X} = a + \frac{1}{2} c$
But the $+ \frac{3}{2} c$ inside the brackets does not match the $+ \frac{1}{2} c$ in $\vec{O X} = a + \frac{1}{2} c$
Therefore you cannot write $\vec{O B}$ and $\vec{O X}$ as scalar multiples of each other

$\vec{O X}$ is not a scalar multiple of $\vec{O B}$
Therefore OX and OB are not parallel
O , X and B cannot be collinear

(b) Maria believes that the point $Y$ , which is three quarters along $A C$ from $A$ , lies on the line $O B$ .

Show that $O$ , $Y$ and $B$ are collinear.

Similarly to part (a), find $\vec{O Y}$ and see if it is parallel to $\vec{O B}$

$\begin{array}{rcl} \vec{O Y} & = & \vec{O A} + \frac{3}{4} \vec{A C} \\ = & 2 a + \frac{3}{4} (- 2 a + c) \\ = & \frac{1}{2} a + \frac{3}{4} c \end{array}$

Use factorisation to write $\vec{O B}$ in terms of $\vec{O Y}$

$\vec{O B} = 2 a + 3 c = 4 (\frac{1}{2} a + \frac{3}{4} c) = 4 \vec{O Y}$

So OB is parallel to OY
They also have a common point, O

$\vec{O B} = 4 \vec{O Y}$
Therefore OY and OB are parallel
They also have a common point, O
Therefore O, Y and B are collinear

Equating Coefficients of Vectors

How do I equate coefficients of vectors?

In the vector $10 a - 3 b$
- the coefficient of a is $10$
- the coefficient of b is $- 3$
Two vectors can only be equal if all their coefficients are equal
So if the vectors $3 a + k b$ and $m a + 5 b$ are both equal
- then $3 = m$ (by equating coefficients of a)
- and $k = 5$ (by equating coefficients of b)

How do I use equating coefficients to find points of intersection?

Some diagrams have vectors that meet at a point
- These are called concurrent vectors
To find this point, create two different vector paths that approach the point from different directions
- Then set them equal and equate coefficients
For example, if the lines AB and CD intersect at the point P , find $\vec{A P}$
- One path is along the line AB
  - A , P and B are collinear
  - so $\vec{A P} = k \vec{A B}$ (they are parallel)
- Another path is along the line CD
  - For example, $\vec{A P} = \vec{A C} + \vec{C P}$
  - C , P and D are also collinear so $\vec{C P} = λ \vec{C D}$
  - $λ$ is a different scalar to $k$
- Set both paths equal and equate coefficients
  - This forms simultaneous equations in $k$ and $λ$
  - Solve these and substitute their values back in to find $\vec{A P}$

Examiner Tips and Tricks

The method of equating two different paths is really useful for other hard situations.
- For example, extending lines out of a diagram, or continuing lines within a diagram.

Worked Example

The diagram shows the diagonals of quadrilateral $O A B C$ , where

$\vec{O A} = 2 a$

$\vec{O C} = c$

You are also given that

$\vec{A B} = 3 \vec{O C}$

The diagonals $A C$ and $O B$ intersect at the point $P$ .

Find the vector $\vec{O P}$ , giving your answer fully simplified in terms of $a$ and $c$ .

Find two different paths from O to P that come in along different diagonals
The first path is along OB itself
Although the length OP is unknown, $\vec{O P}$ is definitely a scalar multiple of $\vec{O B}$ (they are parallel)

$\vec{O P} = k \vec{O B}$

Use $\begin{array}{rcl} \vec{O B} & = & \vec{O A} + \vec{A B} = \vec{O A} + 3 \vec{O C} \end{array}$ to write this first path in terms of a and c

$\vec{O P} = k (2 a + 3 c)$

The second path needs to come in along the AC diagonal

$\begin{array}{rcl} \vec{O P} & = & \vec{O A} + \vec{A P} \end{array}$

Although the length AP is unknown, $\vec{A P}$ is definitely a scalar multiple of $\vec{A C}$ (they are parallel)
Give the scalar a letter different to $k$ used above

$\begin{array}{rcl} \vec{O P} & = & \vec{O A} + λ \vec{A C} \end{array}$

Use $\vec{A C} = \vec{A O} + \vec{O C}$ to write this second path in terms of a and c

$\vec{O P} = 2 a + λ (- 2 a + c)$

Set the first path equal to the second path

$k (2 a + 3 c) = 2 a + λ (- 2 a + c)$

Collect the terms into their a and c components on each side

$2 k a + 3 k c = (2 - 2 λ) a + λ c$

Equate (and simplify) the a coefficients

$\begin{array}{rcl} 2 k & = & 2 - 2 λ \\ k & = & 1 - λ \end{array}$

Equate the c coefficients

$3 k = λ$

This gives two simultaneous equations in $k$ and $λ$
Solve these simultaneously

$\begin{array}{rcl} k & = & 1 - 3 k \\ 4 k & = & 1 \\ k & = & \frac{1}{4} \end{array}$
and $λ = \frac{3}{4}$

Go back to either of the two paths for $\vec{O P}$
Substitute in $k$ or $λ$
Simplify to get the final answer

$\begin{array}{rcl} \vec{O P} & = & k (2 a + 3 c) \\ = & \frac{1}{4} (2 a + 3 c) \\ = & \frac{1}{2} a + \frac{3}{4} c \end{array}$

$\begin{array}{rcl} \vec{O P} & = & \frac{1}{2} a + \frac{3}{4} c \end{array}$

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Magnitude of a VectorNext:Introduction to Derivatives

Geometric Proof with Vectors (Edexcel IGCSE Further Pure Maths): Revision Note

Vector Paths

How do I use vector paths?

How do I use ratios in vector paths?

Parallel Vectors

How do I know if two vectors are parallel?

How do I use factorisation to show two vectors are parallel?

Collinearity

What does collinear mean?

How do I use vectors to show that three points are collinear?

How can collinearity be used when extend lines?

Equating Coefficients of Vectors

How do I equate coefficients of vectors?

How do I use equating coefficients to find points of intersection?

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Logarithms, Indices & Surds

Logarithms, Indices & Exponentials

Exponential Functions

Logarithmic Functions

Properties of Indices

Properties of Logarithms

Solving Exponential Equations

Surds

Simplifying Surds

Rationalising Denominators

Equations, Identities & Inequalities

Quadratic Functions

Factorising Quadratics

Completing the Square

Solving Quadratic Equations

Roots of Quadratic Equations

Equations & Identities

Algebraic Division

Factor & Remainder Theorems

Solving Cubic Equations

Simultaneous Equations

Inequalities

Solving Inequalities

Graphs of Inequalities

Coordinate Geometry & Graphs

Coordinate Geometry

Basic Coordinate Geometry

Equations of a Straight Line

Graphs

Graphing Functions

Graphs of Polynomials

Graphs of Rational Functions

Solving Equations Graphically

Series

Arithmetic & Geometric Series

Sigma Notation

Arithmetic Sequences & Series

Geometric Sequences & Series

Binomial Series

Binomial Expansion

General Binomial Expansion

Applications of Binomial Expansion

Geometry & Trigonometry

Radians

Radian Measure

Arcs & Sectors

Trigonometric Ratios

Basic Trigonometry

Sin, Cos & Tan

Graphs of Trigonometric Functions

Trigonometric Formulae & Identities

Sine & Cosine Formulae

Trigonometric Identities

Trigonometric Addition Formulae

Trigonometric Equations

Linear Trigonometric Equations

Quadratic Trigonometric Equations

Vectors

Vectors

Vector Basics

Position & Displacement Vectors

Magnitude of a Vector

Geometric Proof with Vectors