IGCSEFurther MathsEdexcelRevision NotesVectorsVectorsMagnitude of a Vector

Magnitude of a Vector (Edexcel IGCSE Further Pure Maths): Revision Note

Exam code: 4PM1

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on

Magnitude of a Vector

How do I find the magnitude of a vector?

  • The magnitude of a vector is its length (distance)

    • It is also called the modulus

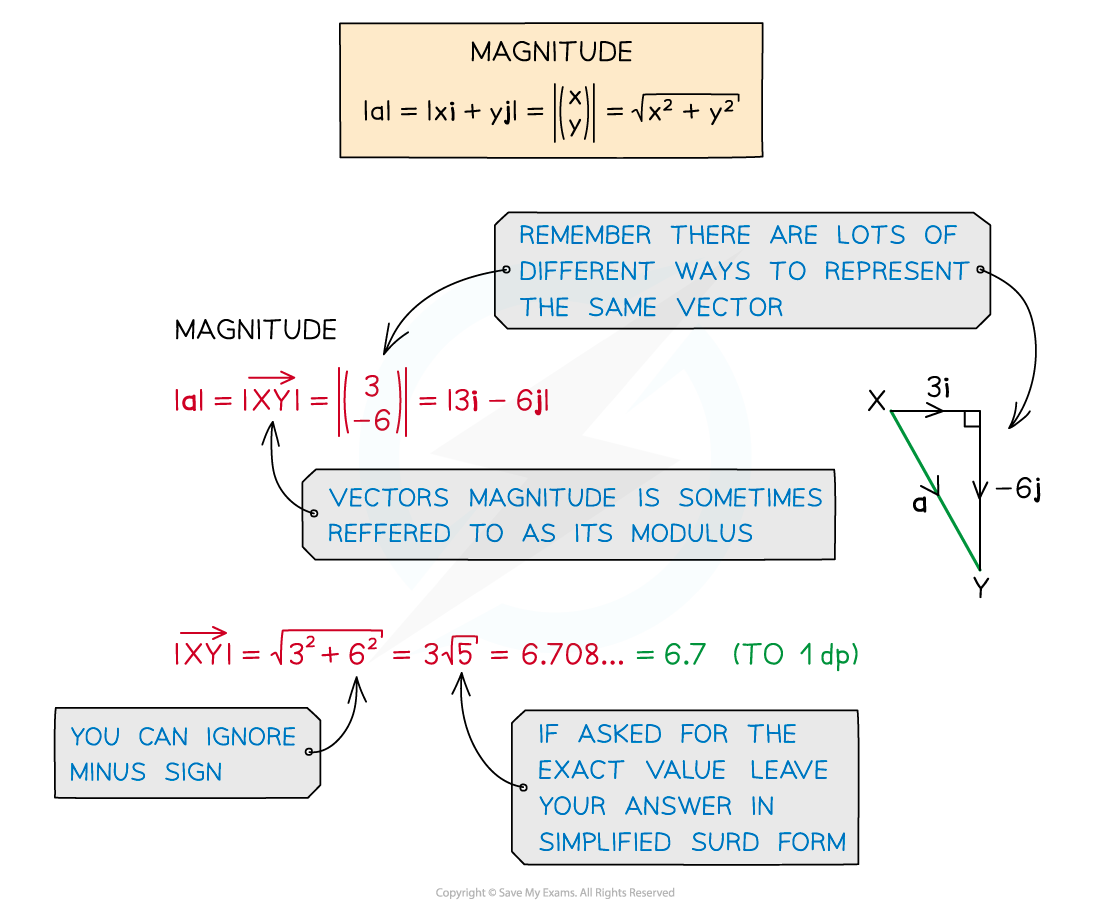
  • The magnitude of stack A B with italic rightwards arrow on top is written open vertical bar stack A B with rightwards arrow on top close vertical bar

    • The magnitude of a is written |a|

  • In component form, the magnitude is the hypotenuse of a right-angled triangle

    • Use Pythagoras' theorem to find it

    • The magnitude of bold a equals x bold i plus blank y bold j is

      • open vertical bar bold a close vertical bar equals blank square root of x to the power of 2 space end exponent plus blank straight y squared end root

      • where bold a equals blank open parentheses table row x row y end table close parentheses

Finding the magnitude of a vector

How do I find harder magnitudes?

  • The magnitude of a sum of vectors is not equal to the sum of the magnitudes

    • vertical line bold a plus-or-minus bold b vertical line not equal to vertical line bold a vertical line plus-or-minus vertical line bold b vertical line

      • Work out a + b (or a - b) first, then find its magnitude 

  • You may need to form an equation

    • For example, |a| = 5 where a = 4i + xj

      • square root of 4 squared plus x squared space end root equals 5

      • This solves to give x equals plus-or-minus 3

How do I find the magnitude of a displacement vector?

  • You can use coordinate geometry to find magnitudes of displacement vectors from A  to B

    • From the position vectors of A  and B  you know their coordinates

      • If  bold a equals stack O A with rightwards arrow on top equals x subscript 1 bold i plus y subscript 1 bold j equals open parentheses table row cell x subscript 1 end cell row cell y subscript 1 end cell end table close parentheses,  then point A has coordinates open parentheses x subscript 1 comma space y subscript 1 close parentheses

      • If  bold b equals stack O B with rightwards arrow on top equals x subscript 2 bold i plus y subscript 2 bold j equals open parentheses table row cell x subscript 2 end cell row cell y subscript 2 end cell end table close parentheses,  then point B has coordinates open parentheses x subscript 2 comma space y subscript 2 close parentheses

    • The distance between two points is given by d space equals blank square root of open parentheses x subscript 1 minus blank x subscript 2 close parentheses squared space plus space open parentheses y subscript 1 minus blank y subscript 2 close parentheses squared end root blank

      • So  open vertical bar stack A B with rightwards arrow on top close vertical bar space equals blank square root of open parentheses x subscript 1 minus blank x subscript 2 close parentheses squared space plus space open parentheses y subscript 1 minus blank y subscript 2 close parentheses squared end root blank

    • For example, if points A and B have position vectors 5 bold i plus 3 bold j and 3 bold i minus 6 bold j respectively

      • then  open vertical bar stack A B with rightwards arrow on top close vertical bar equals square root of open parentheses 5 minus 3 close parentheses squared plus open parentheses 3 minus open parentheses negative 6 close parentheses close parentheses squared end root equals square root of 85 equals 9.22 space open parentheses 3 space straight s. straight f. close parentheses

  • Alternatively, you could find open vertical bar stack A B with rightwards arrow on top close vertical bar by

    • first using  stack A B with rightwards arrow on top equals negative stack O A with rightwards arrow on top plus stack O B with rightwards arrow on top to find stack A B with rightwards arrow on top in vector form

      • and then calculating its magnitude directly

    • See the Worked Example below 

Examiner Tips and Tricks

  • When magnitudes involve algebra, it helps to square both sides to get rid of the square root sign!

Worked Example

O, Aand B are fixed points, where stack O A with rightwards arrow on top equals 2 bold i plus m bold j and stack O B with rightwards arrow on top equals negative bold i plus 4 bold j.

Given that vertical line stack A B with rightwards arrow on top vertical line equals 3 square root of 2 and m greater than 5, find the value of m. 

Use  stack A B with rightwards arrow on top equals stack A O with rightwards arrow on top plus stack O B with rightwards arrow on top equals negative stack O A with rightwards arrow on top plus stack O B with rightwards arrow on top
Simplify and collect components 

table row cell stack A B with rightwards arrow on top end cell equals cell negative open parentheses 2 bold i plus m bold j close parentheses plus open parentheses negative bold i plus 4 bold j close parentheses end cell row blank equals cell negative 2 bold i minus m bold j minus bold i plus 4 j end cell row blank equals cell negative 3 bold i plus open parentheses 4 minus m close parentheses bold j end cell end table
 

Use  vertical line x bold i plus y bold j vertical line equals square root of x squared plus y squared end root 

table row cell open vertical bar stack A B with rightwards arrow on top close vertical bar end cell equals cell square root of open parentheses negative 3 close parentheses squared plus open parentheses 4 minus m close parentheses squared end root end cell end table
 

Expand and simplify inside the square root
You cannot just take the square root of the individual terms!
 

table row cell open vertical bar stack A B with rightwards arrow on top close vertical bar end cell equals cell square root of 9 plus 16 minus 8 m plus m to the power of 2 space end exponent end root end cell row blank equals cell square root of 25 minus 8 m plus m to the power of 2 space end exponent end root end cell end table
 

Substitute in open vertical bar stack A B with rightwards arrow on top close vertical bar equals 3 square root of 2 from the question
Square both sides and form a quadratic in m
 

table row cell 3 square root of 2 end cell equals cell square root of 25 minus 8 m plus m squared end root end cell row cell open parentheses 3 square root of 2 close parentheses squared end cell equals cell 25 minus 8 m plus m squared end cell row 18 equals cell 25 minus 8 m plus m squared end cell row 0 equals cell m squared minus 8 m plus 7 end cell end table
 

Factorise and solve 

0 equals open parentheses m minus 1 close parentheses open parentheses m minus 7 close parentheses m equals 1 comma space space m equals 7
 

You are given that m greater than 5 in the question
This means m equals 7 is the only valid answer

bold italic m bold equals bold 7

Unit Vectors

What is a unit vector?

  • A unit vector is a vector of length 1

  • Any vector, a, can be made a unit vector by dividing it by its magnitude,fraction numerator bold a over denominator open vertical bar bold a close vertical bar end fraction

    • This will result in a vector of length 1

      • It still points in the same direction as a

  • For example, to make 3i – 4j a unit vector

    • find its magnitude, square root of 3 squared plus open parentheses negative 4 close parentheses squared end root equals square root of 25 equals 5

    • divide by its magnitude

      • fraction numerator left parenthesis 3 bold i blank minus 4 bold j right parenthesis over denominator 5 end fraction equals 3 over 5 bold i minus 4 over 5 bold j blank

      • Each component is divided by the magnitude

Examiner Tips and Tricks

  • Read vector questions carefully

    • Some may want you to give your final answer as a unit vector!

Worked Example

The position vector of a point, A, relative to the origin, O, is given by stack O A with rightwards arrow on top equals negative 7 bold i plus bold j 

Find a unit vector in the direction of stack O A with rightwards arrow on top, giving your answer in exact form.

 

To find a unit vector, divide the vector by its magnitude
Find and simplify the magnitude, vertical line stack O A with rightwards arrow on top vertical line, using square root of x squared plus y squared end root
 

table row cell vertical line stack O A with rightwards arrow on top vertical line end cell equals cell square root of open parentheses negative 7 close parentheses squared plus 1 squared end root end cell row blank equals cell square root of 49 plus 1 end root end cell row blank equals cell square root of 50 end cell row blank equals cell square root of 25 cross times 2 end root end cell row blank equals cell 5 square root of 2 end cell end table
 

Divide each component in stack O A with rightwards arrow on top by table attributes columnalign right center left columnspacing 0px end attributes row blank blank cell 5 square root of 2 end cell end table
 

fraction numerator stack O A with rightwards arrow on top over denominator vertical line stack O A with rightwards arrow on top vertical line end fraction equals negative fraction numerator 7 over denominator 5 square root of 2 end fraction bold i plus fraction numerator 1 over denominator 5 square root of 2 end fraction bold j

The unit vector is bold minus fraction numerator bold 7 over denominator bold 5 square root of bold 2 end fraction bold i bold plus fraction numerator bold 1 over denominator bold 5 square root of bold 2 end fraction bold j

negative fraction numerator 7 over denominator square root of 50 end fraction bold i plus fraction numerator 1 over denominator square root of 50 end fraction bold j would be accepted
Decimals would not be accepted
Rationalised denominators would be accepted, negative fraction numerator 7 square root of 2 over denominator 10 end fraction bold i plus fraction numerator square root of 2 over denominator 10 end fraction bold j

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student

Did this page help you?

Previous:Position & Displacement VectorsNext:Geometric Proof with Vectors
Author
Reviewer
Mark Curtis

Author: Mark Curtis

Expertise: Maths Content Creator

Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Subject Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Magnitude of a Vector