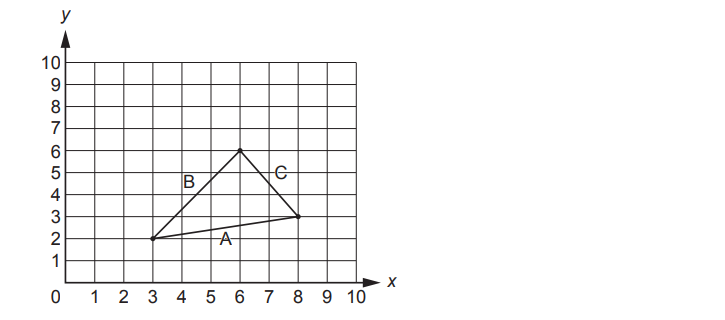
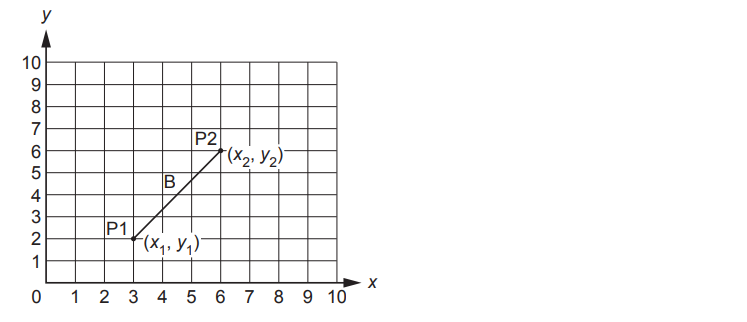Three points on a grid form a triangle with sides of length A, B and C as shown in the example:
A triangle is said to be right-angled if the following test is true (where A is the length of the longest side):
A2 = B2 + C2
A2 means A multiplied by A, for example 32 means 3 × 3 which evaluates to 9
You can calculate A2, B2 and C2 by using the coordinates of the endpoints of each line.
For example, B2 is calculated as follows:
The endpoints, P1 and P2, have the coordinates (3, 2) and (6, 6).
The value B2 is given by the formula:
B2 = (x1 − x2) 2 + (y1 − y2) 2
In this example:
B2 = (3 − 6)2 + (2 − 6)2
B2 = (–3)2 + (–4)2
B2 = 9 + 16
B2 = 25
The test used to check if a triangle is right-angled can be written in two ways:
A2 = B2 + C2
or
A = √(B2 + C2)
The symbol √ represents the square root operation. For example, √81 = 9
A new function SQRT() is written to perform the square root operation. The function takes an integer number as a parameter and returns a positive real value representing the square root of the number.
During testing it is found that the SQRT() function returns a value that is only accurate to 4 decimal places.
For example, SQRT(25) returns 5.0000125 rather than the correct value of 5.0
The function IsRA() from part (a) is modified to use the new SQRT() function to test if a triangle is right-angled.
Describe a problem that might occur when using the modified IsRA() function and suggest a solution that still allows the SQRT() function to be used.