Inverse Functions (DP IB Applications & Interpretation (AI): SL): Revision Note

Inverse Functions

What is an inverse function?

• An inverse function, $f^{-1}\left(x\right)$, reverses (or undoes) the effect of $f\left(x\right)$

  • for example

    • if $f\left(x\right)=2x$ then $f^{-1}\left(x\right)=\frac{x}{2}$

    • if $g\left(x\right)=x+10$ then $g^{-1}\left(x\right)=x-10$

• Inverse functions can be used to solve equations

  • e.g. the solution of $f\left(x\right)=8$ is $x=f^{-1}\left(8\right)$

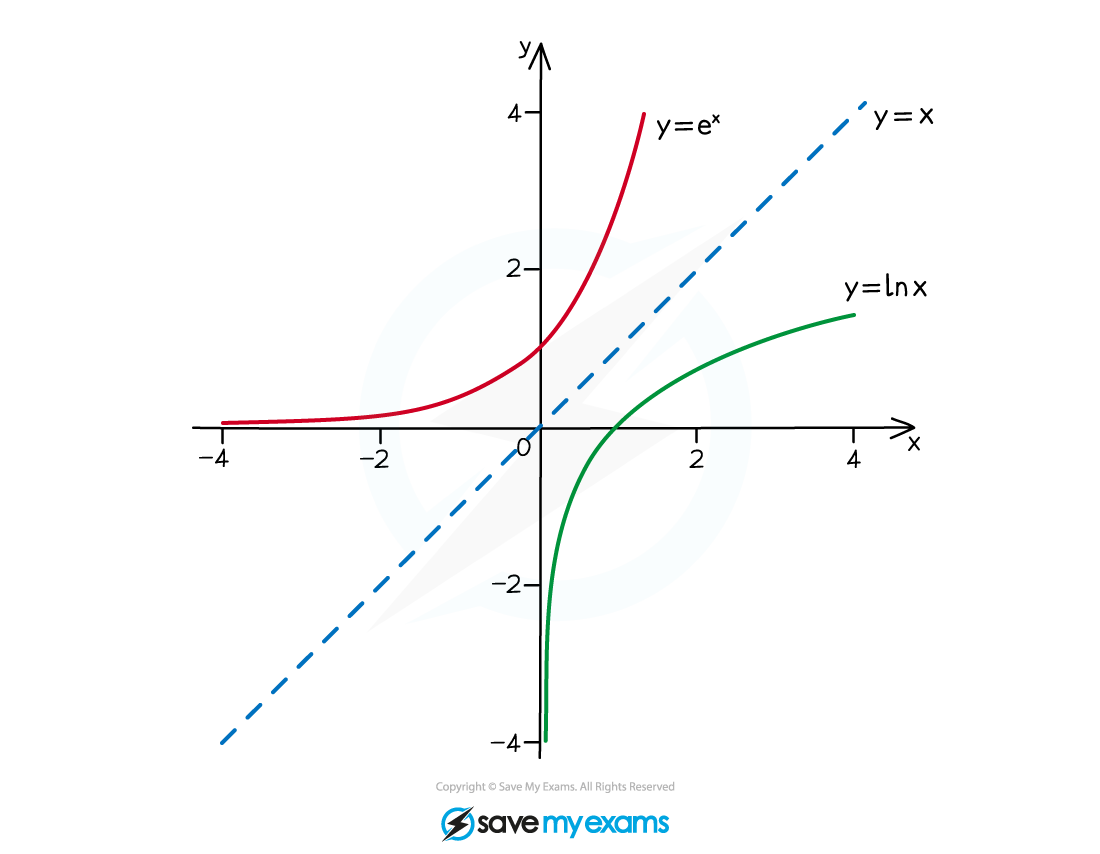
How do I sketch an inverse function?

• The graph of $y=f^{-1}\left(x\right)$ is a reflection of the graph $y=f\left(x\right)$ in the line $y=x$

  • e.g. if $f\left(x\right)=2x$ and $f^{-1}\left(x\right)=\frac{x}{2}$

    • then $y=2x$ and $y=\frac{1}{2}x$

    • which reflect in $y=x$

• If $y=f\left(x\right)$ intersects $y=x$ then $f^{-1}\left(x\right)$ also intersects $y=x$ at the same point

  • i.e. solutions to either $f\left(x\right)=x$ or $f^{-1}\left(x\right)=x$

    • are solutions to $f\left(x\right)=f^{-1}\left(x\right)$

  • There may be other solutions to $f\left(x\right)=f^{-1}\left(x\right)$ that don't lie on the line $y=x$

How do I find the domain and range of an inverse function?

• The domain of a function becomes the range of its inverse

  • e.g. if $f\left(x\right)=2x$ has domain $1\le x\le 3$

    • then the range of $f^{-1}\left(x\right)$ is $1\le f^{-1}\left(x\right)\le 3$

• The range of a function becomes the domain of its inverse

  • e.g. if $f\left(x\right)=2x$ has range $2\le f\left(x\right)\le 6$

    • then the domain of $f^{-1}\left(x\right)$ is $2\le x\le 6$

What condition is needed for an inverse function to exist?

• For an inverse function $f^{-1}\left(x\right)$ to exist

  • the original function $f\left(x\right)$ must be one-to-one

• This ensures $f^{-1}\left(x\right)$ never gives out two or more outputs

  • which functions are not allowed to do