IBPhysicsDPHLExam QuestionsSynoptic AssessmentData-Based Questions (Paper 1B)

Data-Based Questions (Paper 1B) (DP IB Physics: HL): Exam Questions

3 hours20 questions

Select a download format for Data-Based Questions (Paper 1B)

Scroll for more

Select an answer set to view for
Data-Based Questions (Paper 1B)

1a
Sme Calculator5 marks

A group of students investigate the rise of a liquid in a capillary tube. The students use a travelling microscope to measure the height h reached by the liquid when one end of the capillary tube is immersed into it.

A travelling microscope is a measuring instrument consisting of a simple microscope that can be moved vertically along a vernier scale. The students take measurements of the positions of the top and bottom of the liquid column.

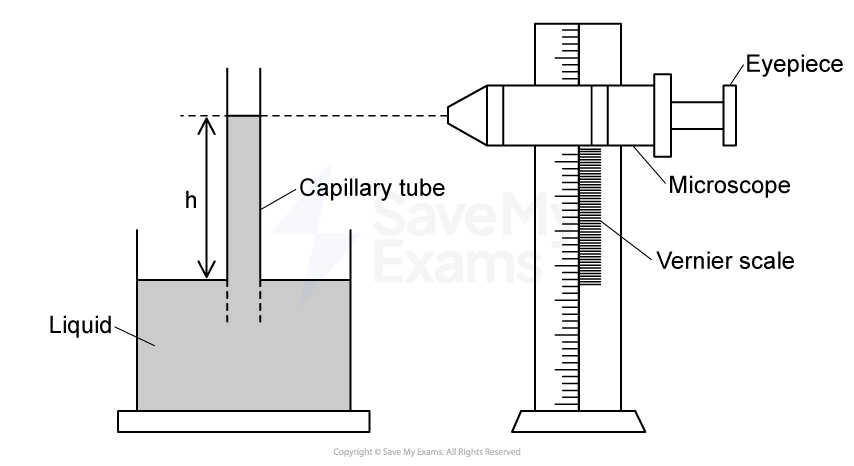
ib-practice-paper-1b-set-a-question-1a

The students used a capillary tube with an internal radius r equal to 0.10 mm and recorded the following readings from the vernier scale.

Bottom of liquid column / cm

Top of liquid column / cm

12.00

27.10

 (i) State the uncertainty in each of these readings.

[1]

(ii) Calculate the percentage uncertainty in the student’s value of h.

[2]

(iii) The students repeated the measurement of h for capillary tubes of different radii. The table shows the student’s final data.

r space divided by space mm

1 over r

h space divided by space cm

0.09

11.1

16.56

0.10

10.0

15.1

0.12

8.3

12.6

0.15

6.7

10.33

 Discuss the values that the students have recorded.

[2]

How did you do?

1b
Sme Calculator6 marks

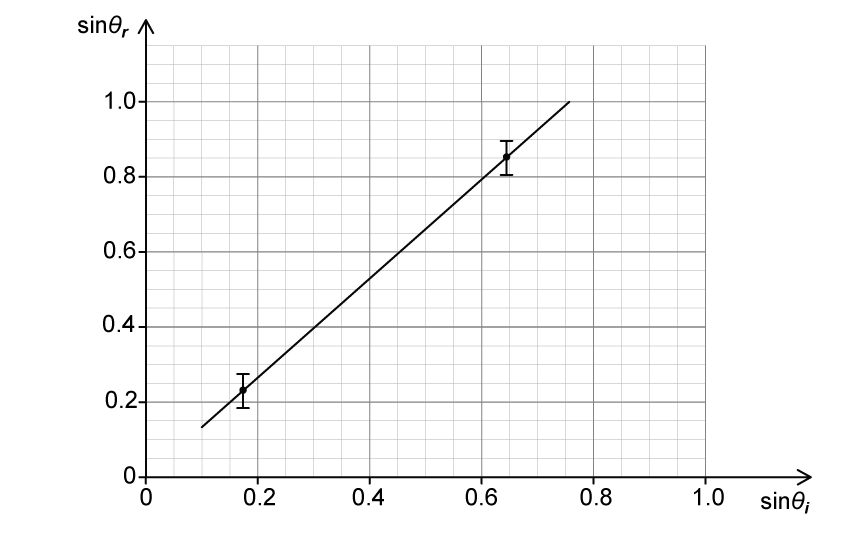
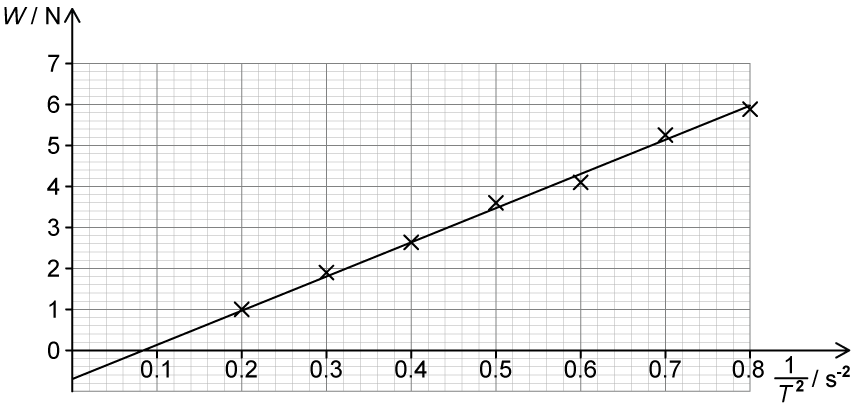
The students suggest the following theoretical relationship between h and r

h space equals space k over r

where k is a constant.

To verify the relationship, the variation of h with 1 over r is plotted.

ib-practice-paper-1b-set-a-question-1b

(i) Determine k by drawing a line of best fit, and state an appropriate unit for k.

[3]

 (ii) Estimate h for a tube with internal radius r = 0.11 mm.

[1]

 (iii) Suggest whether the student’s data supports the theoretical relationship.

[2]

How did you do?

2a
Sme Calculator3 marks

A group of students investigate the circular motion of a small coin on a horizontal turntable. The turntable is connected to a driver unit which rotates it at a constant rate.

ib-practice-paper-1b-set-b-question-1a1

The group measures the distance r between the centre of the turntable and the centre of the coin with a metre rule as shown.

ib-practice-paper-1b-set-b-question-1a

Show that the percentage uncertainty in the value of r is about 1%.

How did you do?

2b
Sme Calculator5 marks

The group switches on the driver unit and increases the rate of rotation until the coin slides off the turntable. 

They record the angular velocity omega of the turntable from a digital display on the driver unit. They then replace the coin in the original position on the turntable and repeat the procedure. The table shows their recorded results.

Reading

1

2

3

4

5

6

ω / rad s-1

0.125

0.112

0.118

0.123

0.116

0.120

(i) Calculate the mean value of omega and its percentage uncertainty.

[3]

(ii) The students used omega and r to calculate the centripetal acceleration of the coin at the instant it started to slide.

Calculate the percentage uncertainty in this centripetal acceleration.

[2]

How did you do?

2c3 marks

The group repeats the procedure with different values of r.

Predict how the value of omega at which the coin starts to slide varies as r is increased.

How did you do?

3a
Sme Calculator4 marks

A group of students use the apparatus shown to determine the viscosity of a liquid. The group measures the force required to pull a small sphere upwards through the liquid at a constant speed.

ib-practice-paper-1b-set-c-question-1a

The group measures the diameter of the sphere using a micrometer.

ib-practice-paper-1b-set-c-question-1a-

(i) Outline one precaution that should be taken when using a micrometer.

[1]

(ii) Determine, from the micrometer reading, the diameter of the sphere and its percentage uncertainty.

[3]

How did you do?

3b1 mark

The drag force F subscript d acting on the sphere and its speed v in the liquid are related by

F subscript d space equals space 6 straight pi eta r v

where eta is the viscosity of the liquid, and r is the radius of the sphere.

Deduce the unit of eta in terms of fundamental SI units.

How did you do?

3c
Sme Calculator3 marks

The group use a force gauge to take measurements of the force on the suspended sphere when it is stationary in the liquid.

ib-practice-paper-1b-set-c-question-1c

When the sphere is stationary, the reading on the force gauge is 0.20 N.

A student moves the force gauge upwards so that the sphere moves at a constant speed. They determined this value of speed by taking the following measurements

  • distance moved between the rubber bands = (25.0 ± 0.1) cm

  • time taken to move between the rubber bands = (0.78 ± 0.02) s

When the sphere is moving at constant speed, the reading on the force gauge is 0.29 N. The buoyancy force is assumed to have a negligible effect.

(i) Outline why it was necessary to take two measurements of force.

[1]

(ii) Show that the value of eta is about 1.7.

[2]

How did you do?

3d
Sme Calculator5 marks

(i) Determine, using appropriate error calculations, which measurement contributes the largest source of uncertainty to the calculated value of eta.

[3]

(ii) State eta with its absolute uncertainty.

[1]

(ii) The expected value of eta is 1.5. Comment on your result.

[1]

How did you do?

4a1 mark

A student conducts an experiment to measure the refractive index of water.

Light from a ray box is directed into a transparent semicircular dish filled with water. The light enters the curved side of the dish, passes through the water and leaves, refracted, at X.

Outline how the student can ensure that the light is not deflected at the curved surface.

How did you do?

4b
Sme Calculator2 marks

The student varies the position of the ray box to obtain data to determine the refractive index of the water. They use a protractor to collect values for the angles of incidence theta subscript i and refraction theta subscript r at X and record them in a table.

Refraction of light through a semi-circular dish filled with water for three positions of a ray box. The ray box emits light into the water through the curved edge, exiting into the air at point X on the flat edge.

(i) One of their measurements is shown. State theta subscript r for this measurement.

[1]

Protractor measuring from 0 to 180 degrees, split into 19 large divisions and 10 small divisions in between. A clockwise scale is on the outer edge and an anticlockwise scale is on the inner edge. A refracted ray passes through 2 small divisions anticlockwise from 50 on the outer edge and 130 on the inner edge.

(ii) One entry from the table is missing. Complete the table.

[1]

θi

θr

sin θi

sin θr

10

13

0.174

0.225

20

27

0.342

0.454

25

34

0.423

0.559

30

42

0.500

35

50

0.574

0.766

40

58

0.643

0.848

How did you do?

4c
Sme Calculator5 marks

The student plots a graph of the variation with the sine of theta subscript i of the sine of theta subscript r .

They add uncertainty bars for sin space theta subscript r for the first and last data point and draw the best-fit line.

Line graph showing sin(θr) versus sin(θi) with two data points and error bars; positive linear trend from (0.15, 0.2) to (0.75, 1.0).

(i) Determine the gradient of the student's best-fit line.

[2]

(ii) Draw on the student's graph the line of maximum gradient.

[1]

(iii) Determine the value of the refractive index of water with its absolute uncertainty.

[2]

How did you do?

5a2 marks

A group of students wants to investigate how the horizontal component of magnetic field strength B subscript H produced by two coils varies with distance.

They position two identical coils of radius r along a common horizontal axis PR so that their planes are vertical. The coils are connected to a DC power supply. The centre of coil 1 is at point Q, and coil 2 is placed so that its centre is a distance r to the right of Q.

They place a sensor on the axis PR to measure B subscript H. The displacement x of the sensor is measured from Q. The current in each coil can be varied and its direction reversed.

Two vertical coils, labelled coil 1 and coil 2, with radius r, positioned on a shared axis PR, separated by a distance r. Two points on axis PR are labelled: Q at the centre of coil 1, and a sensor a distance x to the right of Q.

Explain why the students placed the sensor on the axis PR.

How did you do?

5b
Sme Calculator2 marks

The students carry out four trials using this arrangement.

  • In trial 1, there is a current in coil 1 only, and the current in coil 2 is zero.

  • In trial 2, there is a current in coil 2 only, and the current in coil 1 is zero.

  • In trial 3, there is a current in both coils so that the magnetic fields produced by the coils are in the same direction.

The magnitudes of the currents in coil 1 and coil 2 are the same in each trial.

The variation with displacement x of B subscript H for trials 1 and 2 is shown. The solid line represents the results from trial 1, while the dotted line represents the results from trial 2.

Graph showing two curves: trial 1 (solid line) peaks at x = 0 with BH = 0.66 mT then declines; trial 2 (dashed line) peaks at x = 68 mm with BH = 0.66 mT. The two curves intersect at around x = 34 mm with BH = 0.48 mT

In trial 3, the resultant B subscript H has a constant maximum value in the region between x space equals space r over 4 and x space equals space fraction numerator 3 r over denominator 4 end fraction.

Determine the value of B subscript H in this region.

How did you do?

5c
Sme Calculator2 marks

In trial 4, the current in coil 2 is reversed so that the direction of the magnetic field produced by coil 2 is also reversed.

The magnitudes of the currents in coil 1 and coil 2 are still the same.

Sketch a graph to show how the resultant B subscript H varies between x space equals space 0 and x space equals space r in trial 4.

Include numerical values on your B subscript H axis that correspond to x space equals space 0 and x space equals space r.

Blank axes: Vertical axis is BH in mT, horizontal axis is x in mm, spanning from 0 to r.

How did you do?

6a5 marks

A student investigates the relationship between centripetal force and period for an object undergoing circular motion.

A rubber bung of mass m is attached to a light, inextensible string, through a tube, to a weight W which hangs vertically. The student swings the bung in a horizontal circular path. The student maintains a constant radius r and varies W. For each value of W, they measure the period T of the motion.

A rubber bung attached to a string spinning in a horizontal circle of radius r, with a weight W hanging vertically through a plastic tube.

For each value of W, the student collects measurements of T six times.

The student obtains the following repeated readings for T for one value of W.

Reading

1

2

3

4

5

6

T / s

1.2

1.4

1.2

1.3

0.8

1.3

(i) Calculate the mean value of T and its percentage uncertainty.

[3]

(ii) Explain how repeated measurements of T reduce random errors but not systematic errors.

[2]

How did you do?

6b1 mark

The variation of W with 1 over T squared is shown.

Graph showing a positive correlation between weight W on the y-axis and 1 over T squared on the x-axis, with data points marked by crosses. The line has a negative y-intercept.

Outline one experimental reason why the graph does not go through the origin.

How did you do?

6c
Sme Calculator4 marks

Theory predicts that, for uniform circular motion, the results are expected to support the relationship

W space equals space fraction numerator 4 straight pi squared m r over denominator T squared end fraction

The radius of the string is measured to be r = (0.600 ± 0.005) m

(i) Suggest an appropriate measuring instrument for determining r.

[1]

(ii) Determine, using the graph, the value of m.

[3]

How did you do?

7a1 mark

A group of students investigates how the maximum force F subscript max exerted by a rebounding ball depends on its internal gauge pressure increment p.

They use a pressure gauge to measure the difference between the atmospheric pressure and the ball's internal pressure. The ball is dropped from a fixed height onto a force sensor that records the maximum force exerted on it during impact.

A ball positioned above a force sensor with a pressure gauge attached to measure internal pressure.

Describe one consideration that must be made when dropping the ball on the force sensor to ensure that the maximum force is measured accurately.

How did you do?

7b
Sme Calculator4 marks

The students systematically increase the gauge pressure and measure F subscript max from a force-time graph displayed on a computer connected to the sensor.

Gauge pressure ∆p / kPa

Maximum force Fmax / N

20

130

40

171

60

189

80

218

100

234

120

250

(i) State one variable that needs to be controlled when collecting the data.

[1]

(ii) Outline how the students determined the value of F subscript max from the force-time graph.

[1]

(iii) By using two sets of data in the table, show that the relationship between F subscript max and p is not directly proportional.

[2]

How did you do?

7c
Sme Calculator5 marks

The students suggest the following relationship between F subscript max and increment p:

F subscript max superscript 3 space equals space k increment p

where k is a constant.

To verify the relationship, the variation of F subscript max superscript 3 with increment p is plotted.

One data point is missing.

Scatter plot showing a positive correlation between maximum force on the y-axis and gauge pressure on the x-axis, with five data points plotted.

(i) Determine the coordinates of the missing point using the original data set and plot it on the graph.

[1]

(ii) The percentage uncertainty in F subscript max is ±3%.

Determine the uncertainty in F subscript max superscript 3 when increment p = 60 kPa and draw the uncertainty bar for this data point on the graph.

[3]

(iii) The SI units of k can be expressed as kg to the power of x space straight m to the power of y space straight s to the power of z.

Determine the values of x, y and z.

[1]

How did you do?

7d1 mark

The students collect only one value of F subscript max for each value of increment p.

Suggest why this is a poor method.

How did you do?

8a1 mark

A student is investigating the properties of a copper wire. To determine its diameter, the student uses a micrometer screw gauge.

Identify one way to ensure that the diameter is measured accurately.

How did you do?

8b
Sme Calculator4 marks

The following data are collected for the wire:

  • Diameter = (0.48 ± 0.01) mm

  • Length = (85.0 ± 0.05) cm

  • Resistance = (0.24 ± 0.02) Ω

Calculate the resistivity of the wire and its absolute uncertainty. State your answers to an appropriate number of significant figures.

How did you do?

8c1 mark

The accepted value for the resistivity of copper at 20°C is 1.7 cross times 10 to the power of negative 8 end exponent   straight capital omega space text m end text .

Comment on whether the wire can be considered pure copper.

How did you do?

9a2 marks

A student investigates the relationship between the length L of a pendulum and its period T of oscillation.

The student makes the following measurements:

Time for 20 oscillations = (28.4 ± 0.2) s

Readings for the length L of the pendulum:

Reading

1

2

3

4

5

6

L / cm

98.2

98.5

98.1

98.7

98.3

98.6

Outline how recording the time for 20 oscillations leads to a more precise measurement of T.

How did you do?

9b2 marks

The student uses a stopwatch to measure the time for 20 oscillations and a millimetre ruler to measure the length of the pendulum.

State, for this experiment

(i) one variable that must be controlled

[1]

(ii) the main source of error in T.

[1]

How did you do?

9c
Sme Calculator4 marks

(i) Calculate the mean length of the pendulum and its percentage uncertainty.

[3]

(ii) Calculate the fractional uncertainty in the period of oscillation.

[1]

How did you do?

9d
Sme Calculator5 marks

The student wants to determine a value for g, the acceleration due to gravity, using the relation

T space equals space 2 straight pi square root of L over g end root

(i) The student plots a graph with T squared on the vertical axis.

State the variable that must be plotted on the horizontal axis in order to obtain a line of best fit that is straight.

[1]

(ii) Outline how g can be determined from this graph.

[2]

(iii) Calculations using the data of the experiment show that g = 9.85681 m s−2 with a percentage uncertainty of 0.5%.

Determine the value of g that can be obtained from this experiment. Include the absolute uncertainty in g to one significant figure.

[2]

How did you do?

10a2 marks

The equation P V space equals space n R T describes the behaviour of an ideal gas.

A student investigates the variation of the volume of a fixed mass of air with temperature to confirm that, for a constant pressure,

V over T space equals space K

where K is a constant.

A sample of air is trapped inside a capillary tube by a small drop of concentrated sulfuric acid that can move freely along the tube. The capillary tube is placed in a beaker of water at room temperature and heated gradually.

The student measures the length l of the column of air and its temperature T.

A capillary tube with labelled open and closed ends. Inside, there's a drop of concentrated sulphuric acid above a sample of trapped air of length l.

(i) State one other measurement that the student will need to make to obtain a value for the volume V of the air sample.

[1]

(ii) Suggest a suitable instrument for this measurement.

[1]

How did you do?

10b5 marks

Five sets of data for this experiment are shown in the table.

T / K

V / 10-5 m3

293

229

303

237

313

246

323

254

333

262

The variation of V with T is shown for four data points.

Scatter plot showing volume (V) in cubic metres, versus temperature (T) in Kelvin. 4 data points trend upwards from 290 K to 330 K.

(i) Plot the missing data point on the graph.

[1]

(ii) Draw the best-fit line on the graph.

[1]

(iii) Explain how the student can use the graph to decide whether the data support the relationship V over T space equals space K.

[3]

How did you do?

10c
Sme Calculator3 marks

(i) Determine K.

[2]

(ii) State an appropriate SI unit for K.

[1]

How did you do?

10d
Sme Calculator1 mark

The pressure of the air is 1.01 cross times 10 to the power of 5 space Pa during the experiment.

Determine the number of moles of air in the sample.

How did you do?