A group of students investigate the motion of a simple pendulum to determine a value for the acceleration of free fall .

The group measures the length of the pendulum with a metre rule and obtains the following repeated readings.
85.5 | 86.0 | 87.5 | 85.5 |
The group divides into two subgroups, A and B, to analyse the data.
Group A quotes the mean value of as 86.125 cm.
Group B quotes the mean value of as 85.7 cm.
Discuss the values that the groups have quoted.
Theory predicts that
Calculate and
.
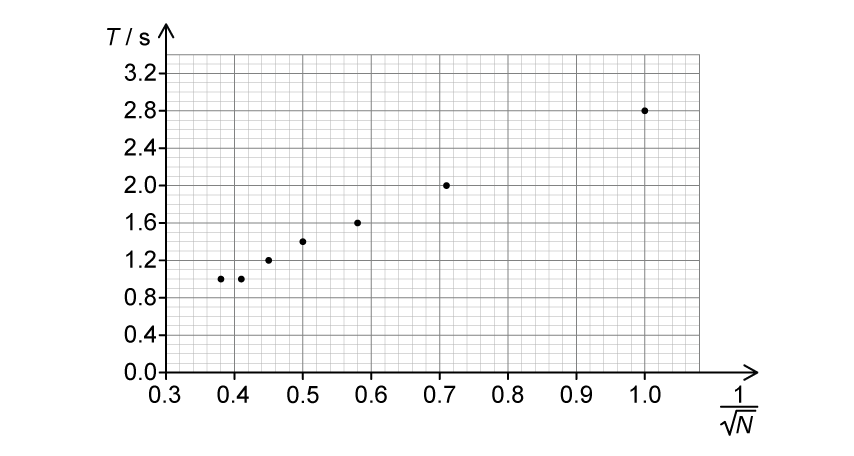
The group sets the pendulum into oscillations with small amplitude and uses a stopwatch to determine the time period.

The stopwatch is started when the pendulum is released at A. Measurements of the time period are taken over 5 oscillations and divided by 5. The procedure is repeated twice and the mean period is determined to be .
(i) Calculate their value of and the percentage uncertainty in this value.
[3]
(ii) Suggest a modification to the method that could reduce the uncertainty in their value of .
[1]
Was this exam question helpful?