The radioactive isotope uranium−238 decays in a decay series to the stable lead−206.
The half−life of is 4.5 × 109 years, which is much larger than all the other half−lives of the decays in the series.
A rock sample, when formed originally, contained 6.0 × 1022 atoms of and no
atoms. At any given time, most of the atoms are either
or
with a negligible number of atoms in other forms in the decay series.
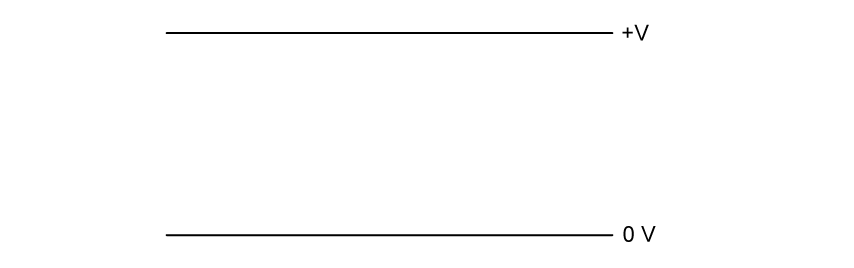
Sketch on the axes below the variation of number of atoms and the number of
atoms in the rock sample as they vary over a period of 1.0 × 1010 years from its formation. Label the lines U and Pb.

A certain time, t, after its formation, the sample contained twice as many atoms as
atoms.
Show that the number of atoms in the rock sample at time t was 4.0 × 1022.
Lead−214 is an unstable isotope of lead−206. It decays by emitting a particle to form bismuth−214 (Bi)
Bismuth is also unstable and has two decay modes:
Emitting an α particle to form thallium−210 (Tl) + energy
Emitting a β particle to form polonium−214 (Po) + energy
(i) Write decay equations for the decay chain of lead−214 to thallium−210 and to polonium−214.
[3]
(ii) Outline the nature of the energy released during this process.
[1]
Natural uranium consists of 99.3% and 0.7%
.
To be used as fuel in a nuclear reactor, natural uranium must be enriched and enclosed in sealed metal containers. The process of enrichment involves increasing the amount of fissile uranium.
Suggest why
(i) natural uranium is not suitable for use as nuclear fuel
[1]
(ii) enrichment is favoured over chemically separating the isotopes from each other.
[2]
When a uranium–235 nucleus undergoes fission, one of the possible reactions is:
The binding energy per nucleon, E, is given in the table below:
Nuclide | E / MeV |
7.60 | |
8.39 | |
8.74 |
A 1500 MW nuclear reactor, operating at 27% efficiency, uses enriched fuel containing 3% uranium–235 and 97% uranium–238. The molar mass of uranium−235 is 0.235 kg mol–1.
Estimate the total mass of original fuel required per year in the nuclear reactor.
Determine the number of fission reactions per day in the nuclear reactor assuming the production of power is continuous.
A nuclear fusion power station uses water as a coolant in its primary cooling circuit. The water enters the reactor core at a temperature of 280°C and absorbs thermal energy from the fusion reactions. The water has a mass flow rate of 2500 kg s-1 and exits the reactor core at 320°C before entering a heat exchanger.
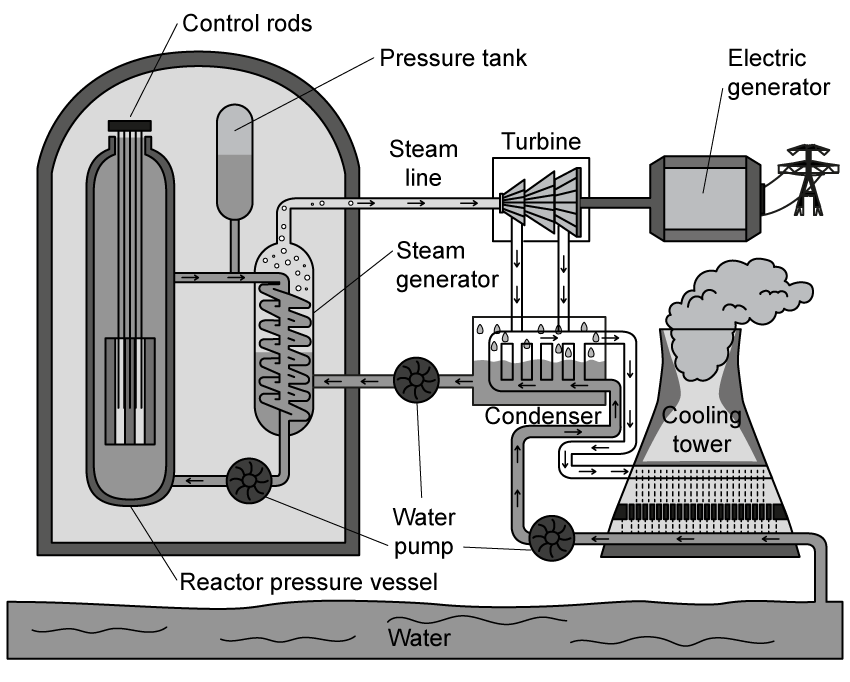
In the steam generator, the water from the primary circuit cools from 320 °C back to 280 °C, and is used to convert secondary circuit water at 25 °C into steam at 100 °C. The specific heat capacity of water is 4200 J kg-1 K-1, and the specific latent heat of vaporisation of water is 2.26 × 106 J kg-1.
Determine the mass of steam that can be produced per second.
Assuming that all the thermal energy from the primary circuit water is transferred to the secondary circuit water, and no thermal energy is lost to the surroundings.
Was this exam question helpful?