Below is the graph of a function , passing through the points P
, Q
, R
and S
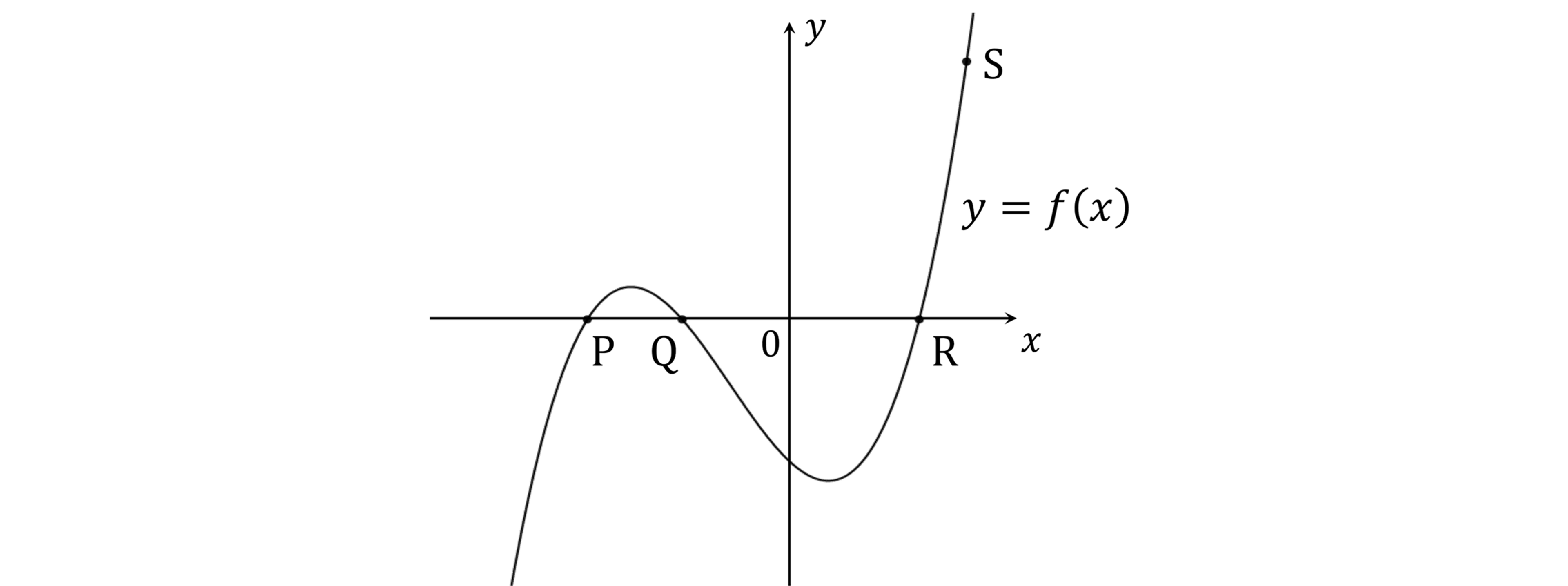
Find the values of and
The function is translated vertically by the vector so that it passes through the point
.
Find the value of
Did this page help you?

